5 刚体单元上限法

2013-05-24

浙江科技学院学报 2013年3期

5 刚体单元上限法

土坡稳定性分析是岩土工程经典问题之一，在铁路、公路、水利水电、建筑基坑及港口码头工程中应用非常广泛。土坡稳定性计算常用的方法是刚体极限平衡法，如Fellenius（1927）提出的圆弧滑动分析方法（瑞典圆弧法），以及改进的毕肖普法（1955）、斯宾塞法（1967）、简布法（1973）、摩根斯坦-普赖斯法（1965）以及萨尔玛法（1973）等。尽管刚体极限平衡法以其简单实用而得到了广泛的应用，但因此方法本身存在一定的局限性，直接导致所取得的解并非总是正确，故其不能解决土体破坏的运动学问题。相反，基于土塑性力学的极限分析上限法，却可以选择机动许可的速度场来寻求土坡的破坏机制（陈祖煜，2002），并且这一方法已被广泛认可和采用。

通过采用极限分析上限法，陈惠发（1975）最早提出了解决均质土坡临界高度的方法，并采用类似土压力系数的稳定数Ns来进行土坡稳定性分析。但这一方法没能推广到非均质土坡问题，也没能给出通用的稳定系数计算公式。Karal（1977）后来对陈惠发的方法进行了改进，得到了旋转破坏机制直接分析评价均质土坡的稳定系数计算公式。Michalowski（1995）则根据极限分析上限法提出了类似条分法的平动破坏机制，并得到了均质土坡计算稳定数Ns的公式。Kumar 和 Samui（2006）还根据非相关联流动法则，采用虚功率方程得出了土坡稳定系数计算公式。

在土质边坡极限分析上限法领域，存在两个明显的问题：其一是不能考虑成层土的非均质特性，其二是没有通用的稳定系数计算公式。正是基于目前存在的问题，笔者提出了将极限分析上限法和有限单元法前处理功能相融合的思想，并通过强度折减法和虚功率方程，实现了求解非均质土坡稳定系数的数值计算方法。

5.1 非均质土坡旋转破坏机构

均质土坡破坏时的机动许可速度场（破坏机构），根据极限分析法可知其可能产生的滑面为一对数螺旋线。对于二维三层土组成的非均质土坡，每一层土可以通过层厚hi、黏聚力ci、内摩擦角φi和容重γi四个参数进行定义（i=1，2，3），其可能滑裂面为通过坡趾的不同对数螺旋线的组合（见图5-1）。

图5-1中三段对数螺旋线滑裂面具有相同的转动中心O，并且相邻两层土交界处，不同对数螺旋线的半径保持不变。每一层土对应的对数螺旋线滑弧，其函数关系可以用内摩擦角表示为

式中：r0，r1，r2，r3和θ0，θ1，θ2，θ3等符号意义参见图5-1，且有

当坡高H和坡度β确定后，通过坡趾的滑裂面Α0Α1Α2C，完全可以由具有共同旋转中心O的分段对数螺旋线确定；而旋转中心O可以由x和y的距离确定，或由θ0和θ3单独确定。

图5-1 非均质土坡旋转破坏机制及速度矢量

5.2 层状土质边坡外力功率计算

陈惠发（1975）在其著作《极限分析与土体塑性》中，推导了均质土坡外力功率计算公式。但对于非均质土坡，常规的解析方法计算外力功率难以实现。笔者根据有限元软件ΑNSYS的前处理功能——网格化，通过三节点三角形单元网格化非均质土体，可以分别计算每一个单元的外力功率。

图5-2所示为滑体经由三角形单元网格化后的效果。从网格化后的滑体中取出编号为i的三角形单元，如图5-3（a）所示，该单元节点编号按逆时针依次为j，k，l，节点坐标分别为（xi，j，yi，j），（xi，k，yi，k），（xi，l，yi，l）。三角形单元（element-i，记为ei）面积计算公式为

图5-2 滑体三角形单元网格化简图

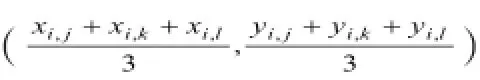
OOei与x轴正方向夹角为

设旋转破坏机构角速度为ω，则编号为i的三角形单元应变速度为

编号为i的三角形单元自重为Wei=γei△ei，所受到的水平地震作用力为khWei，如图5-3（b）所示。外力作用在应变速度vei所做的外功率为

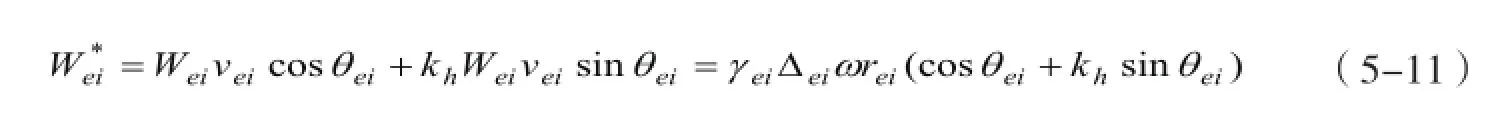
同理，可以计算得到所有单元在应变速度场v所做的外功率为

图5-3 刚体单元计算外力功率

5.3 对数螺旋线组合滑面内能耗散计算

根据极限分析上限法对土质边坡稳定分析的假定，滑体将被视为刚体，而滑裂面被视为速度间断面。因此在滑体内将不存在内能的耗散，换言之，旋转机构的内能耗散集中于组合对数螺旋线上。以图5-1所示的三层土质边坡为例，首先计算第一层土对数螺旋线Α0Α1段的内能耗散，取微分长度rdθ/cosφ1，此长度内的黏聚力为c1rdθ/cosφ1，则黏聚力沿滑裂面的总内能耗散积分表达式为

同理，可以计算得到第二层土对数螺旋线Α1Α2段和第三层土对数螺旋线Α2C段的内能耗散分别为：

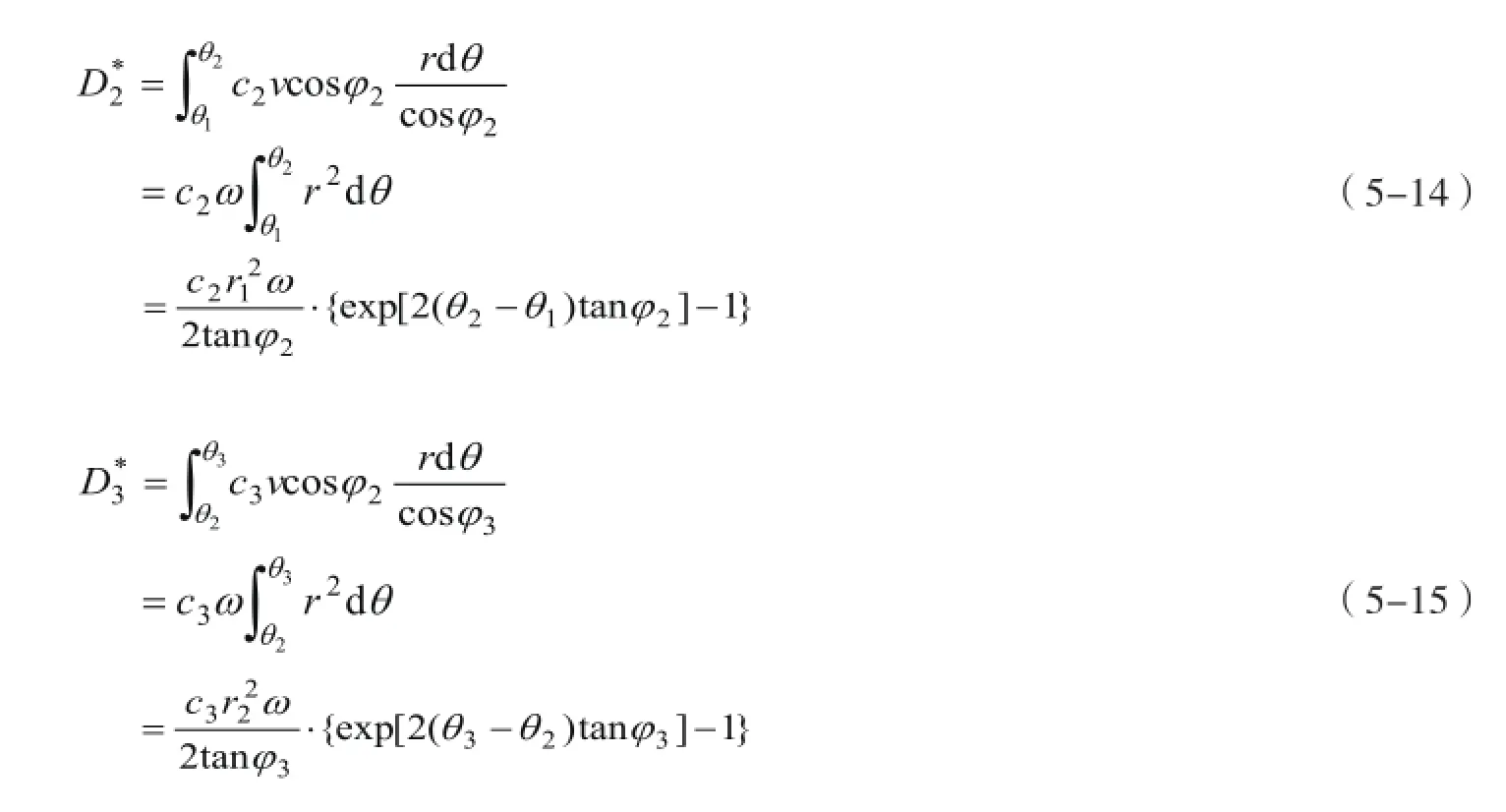
根据数学归纳法，可以得到第i层土的内能耗散计算公式

边坡滑体包括多层土时，则组合对数螺旋线总内能耗散为：

5.4 刚体单元法稳定系数上限解

在极限状态下，多层土组成的非均质边坡虚功率方程为

将式（5-11）、式（5-16）和式（5-18）代入上式，可得

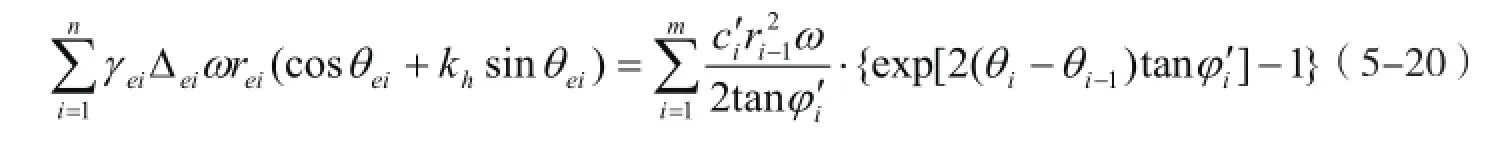
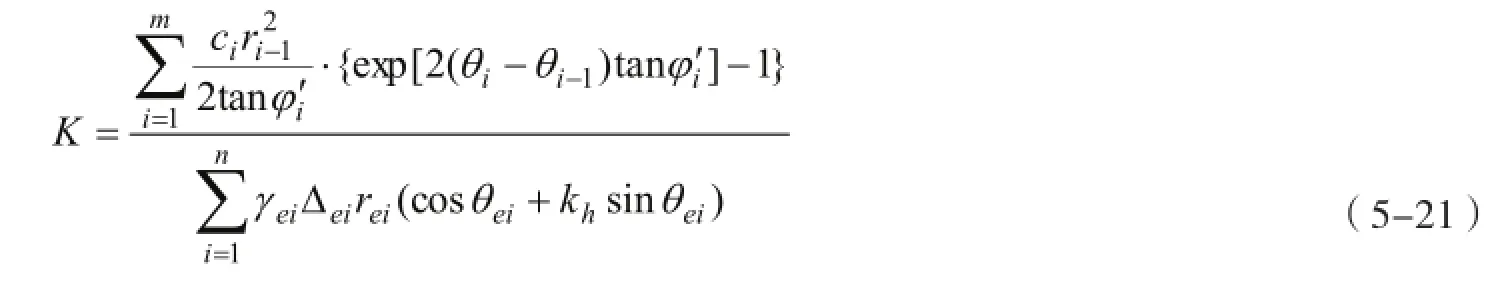
式中：

式（5-21）即为求解非均质土坡稳定性稳定系数的刚体单元上限法计算公式。由于稳定系数K是以隐式出现的，因此需要通过迭代的算法求解。在计算时，先假设一个初始的稳定系数K，应用迭代计算直至前后两次稳定系数K值满足所要求的计算精度为止。一般来说对于满足条件的情况，迭代都是收敛的。

采用刚体单元上限法计算非均质土坡稳定系数的步骤为：① 通过ΑNSYS有限元软件对非均质边坡建模，并进行三角形单元剖分；② 输出节点文件（包括节点号和节点坐标）和单元文件（包括单元编号和单元对应节点号）；③ 编程计算所有单元在重力及地震作用力下产生的外力功率；④ 采用强度折减法，计算每层土对应的对数螺旋线内能耗散；⑤ 通过式（5-21）多次迭代获得刚体单元上限法稳定系数最终解。

以某一两层土组成的非均质土坡为例，坡高8m，坡比1∶1.3，从坡顶到坡脚土体分两层，分别记为第①层和第②层，厚度各4m，土层参数见表5-1。通过采用刚体极限平衡法（对应圆弧滑面）和刚体单元上限法（对应分段对数螺旋线滑面）两种不同方法搜索最危险滑移面，得到图5-4中显示的结果。

表5-1 双层土质边坡土层参数

图5-4 双层土质边坡剖面

刚体极限平衡法分别选用瑞典条分法、毕肖普法和简布法，在自重作用下，稳定系数分别为0.96，1.00和1.00（表5-2）。在相同条件下，刚体单元上限法得到的稳定系数为1.01。从计算结果来分析，两者均可以得到边坡处于临界破坏状态的结论，但文中方法略比刚体极限平衡法结果要大。同样，考虑Ⅶ度地震烈度、Ⅷ度地震烈度和Ⅸ度地震烈度，计算结果均显示边坡将产生破坏，但稳定系数也呈现比刚体极限平衡法略大。

表5-2 不同方法的稳定系数计算结果

通过四种方法得到的稳定系数与地震烈度的敏感性分析来看（见图5-5），文中方法曲线斜率要小于刚体极限平衡法。采用最小二乘法对以上数据进行函数拟合，得到表5-3的稳定系数——地震烈度的经验函数关系。综合分析，可以得到三点结论：①刚体单元上限法稳定系数对地震烈度的敏感性要小于其他三种方法；②随着地震烈度的增加，四种方法得到的稳定系数对地震烈度的敏感性均有所提高；③毕肖普法地震烈度敏感性最大。分析计算结果显示，文中方法和毕肖普法可以代表稳定系数的上限和下限。因此，通过多种方法计算稳定系数时，在界定了上限和下限后，合理选用稳定系数对边坡工程非常重要。