矢量值函数共轭解析的充要条件

晋守博

(宿州学院数学与统计学院，安徽宿州234000)

0 引 言

复变函数起源于19世纪，起初它研究的中心对象是解析函数，解析函数理论在解决平面无源无旋场的问题时能够显示巨大的威力，但对有源场或有旋场却无能为力，到了20世纪30年代，相继出现了准解析函数和广义解析函数，尽管理论上得到了很多结果，但通常十分繁琐，并且至今在力学、物理学上找不到明显的背景，到了1988年王见定在文献［1］首次提出了共轭解析函数的概念，这是一种与解析函数对称的复变函数，他可以描述无源场或无旋场，共轭解析函数的提出使复变函数达到了对称完美，共轭解析函数可以用来解决解析函数所能解决的所有问题，并且比解析函数更加直观方便.文献［2］讨论了这种函数在力学上的初步应用，介绍了共轭解析函数的物理背景.然而，上述关于共轭解析函数的讨论都局限在复变函数的范围内，而关于矢量值函数的讨论也仅仅局限于矢量值解析函数的讨论，很少有涉及矢量值共轭解析函数的内容.

本文将给出一种从复平面到Banach空间的矢量值共轭解析函数，分析矢量值函数共轭解析的充要条件，对于复变函数共轭解析的充要条件文献［3］和［4］分别从指数形式和复形式两个不同方面进行了详细的讨论，关于复值共轭解析函数的进一步讨论可以参考文献［1］.

王见定在文献［1］中给出了如下共轭导数与共轭积分的概念.

定义1 设复变函数w=f(z)在区域D内有定义，给自变量z=x+iy∈D以增量△z=△x+△yi使(z+△z)∈D并计算由自变量所引起的复变函数w=f(z)的增量:

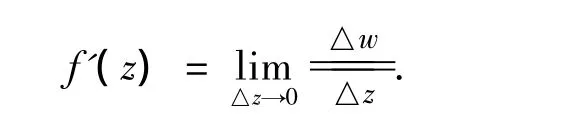
这时称复变函数f(z)在点z共轭可导或共轭可微.

若复变函数w=f(z)在区域D内处处共轭可导，则称f(z)为区域D内的共轭解析函数，或称f(z)在区域D内共轭解析.

根据以上复变函数共轭解析的定义以及矢量值函数解析［5］的概念，我们引入如下矢量值函数共轭解析与共轭积分的定义.

定义2 从复平面的开子集U到Banach空间X中的矢量值函数x(z)称为弱共轭解析的，是指对任意的f∈X*，f(x(z))是U中的复值共轭解析函数;x(z)称为强解析的，是指对任意的z∈U，x(z)在z处强可导，即存在x'(z)∈X，使得

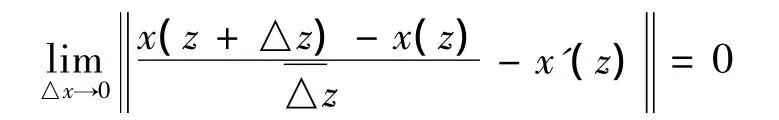
1 主要结论与证明

为了讨论矢量值共轭解析函数的充要条件，首先给出下面两个引理.

引理1 “弱共轭解析”等价于“强共轭解析”.

证明 必要性是显然的，强共轭解析可以推出弱共轭解析.

对于充分性的证明，可以设x(z)在U中弱共轭解析，对任意固定的z∈U、z+△z∈U，取U中的周线(即逐段光滑的简单闭曲线)Γ包围z，z+△z，于是由共轭解析函数的柯西积分公式，对任意的f∈X*，有

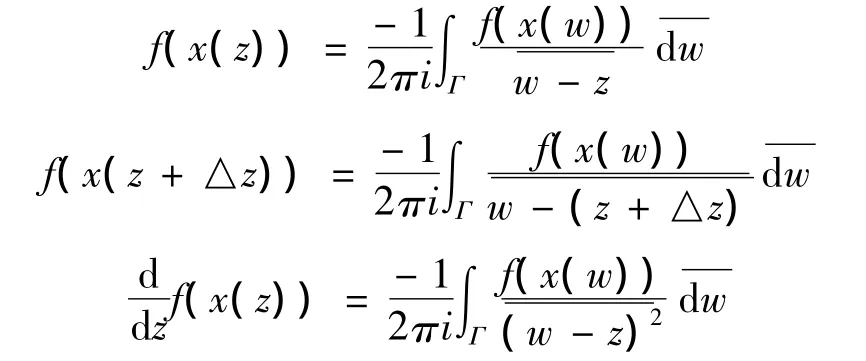
因此对每个f∈X*，有f(x(w))是Γ上的有界函数，以及一致有界定理

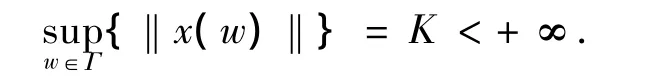
所以

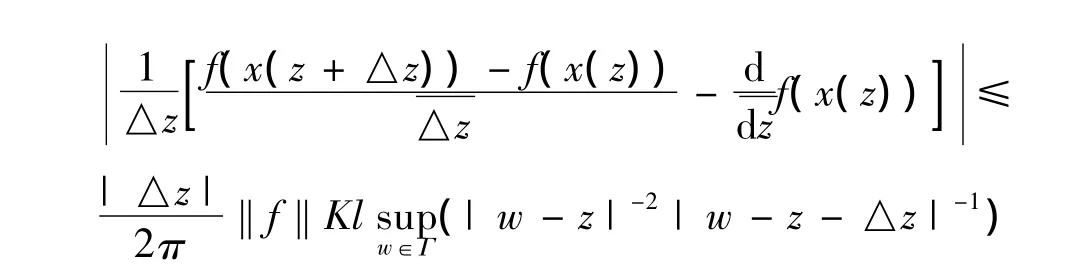
其中l表示曲线Γ的长度，当△z→0时，上式右边趋于0，且对‖f‖≤1是一致的，从而x(z)在z处强共轭可导.

根据引理1，下面我们可以不加区别地直接说共轭解析.

引理2 设x(z)是从复平面的开子集U到Banach空间X的共轭解析函数，z∈U，Γ是U中包围z的周线，则对任意的正整数n，x(z)在z处是n次强共轭可导的，且

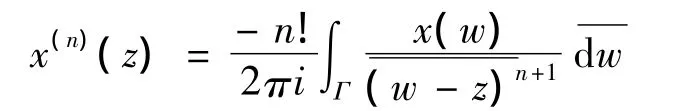
证明 对任意的f∈X*，f(x'(z))=f'(x(z))是U中的共轭解析函数，因此x'(z)是U中的弱共轭解析函数，从而由引理1知，x'(z)在U上是强共轭解析的，依此类推，x(n)(z)也是U中的强共轭解析函数，此外，对任意的f∈X*，有

现在通过上面两个引理来讨论矢量值函数共轭解析的充要条件.

定理1 矢量值函数x(z)在区域G上共轭解析的充要条件为

(1)x(z)在区域G上连续.

证明(必要性)设矢量值函数x(z)在区域G上共轭解析，显然有x(z)在区域G上连续.

另外由函数x(z)的连续性可知，x(z)在周线Γ上一致连续，又因为周线是可求长的，所以矢量值函数的共轭积分存在，且对任意的f∈X*，有

(充分性)对任意的f∈X*，由x(z)的连续性可知，f(x(z))在区域G上也连续，并且由已知条件(2)可得

由复值函数共轭解析的充要条件［1］可知，f(x(z))在区域G上共轭解析.再利用引理1可得，矢量值函数x(z)在区域G上共轭解析.

定理2 如果x(z)是取值于Banach空间X上而在{z;|z－z0|＜r}中共轭解析，则有共轭幂级数展开式

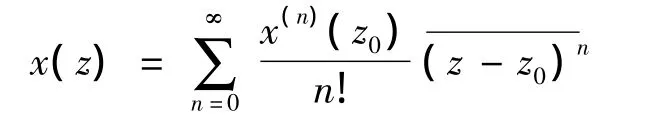
且级数依范数是绝对收敛的，同时在{z;|z－z0|＜r}内依范数内闭一致收敛.

反之，如果x(z)在{z;|z－z0|＜r}上可以表示成依范数绝对收敛的级数

则x(z)在{z;|z－z0|＜r}上是共轭解析的，且

证明 设0 ＜ ρ＜ ρ1＜ r，K=sup{‖x(z)‖;|z－z0|= ρ1}.依引理2

由此可见，级数

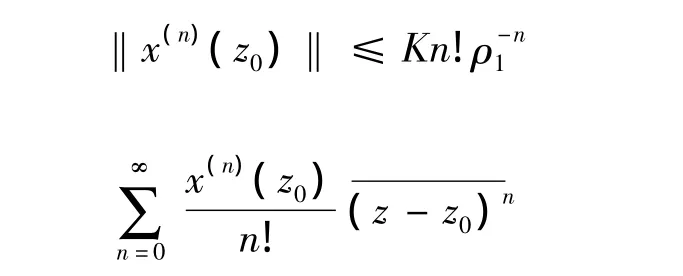
在圆{z;|z－z0|≤ρ}中依范数绝对一致收敛.

对任意的f∈X*，由复值函数的共轭幂级数展式可得

从而

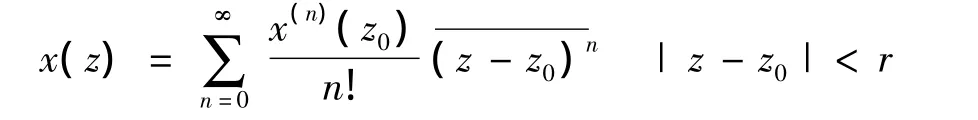
反之，对任意的f∈X*，有

所以f(x(z))在圆|z－z0|＜r内共轭解析，且

从而x(z)在{z;|z－z0|＜r}上是共轭解析的，且

推论1 矢量值函数x(z)在区域G内共轭解析的充要条件为x(z)在区域G内任何一点z0的邻域内可展成的幂级数.

证明 由定理2容易得到上面结论.

关于解析函数和共轭解析函数的应用，目前结论比较少，文献［6］讨论了一类算子值解析函数族的极值点，展示了矢量值解析函数的一些应用.我们将引用文献［2］的例子，简单地介绍一下在特殊情况下矢量值共轭解析函数的应用，当Banach空间X为全体复数时，在这种情况下，矢量值共轭解析函数有比较明确的物理意义，下面来看一个稳定平面流动的例子.

例1 我们用共轭解析函数描述以等速c从平面的左方向右方的流动，显示，此流动的流线cy=c1和等势线cx=c2，我们可以用共轭解析函数f(z)=cx－icy来表示此流动，并称它为此流动的复形.它的共轭导数为:f'(z)=c刚好是流动的速度.

在静电场中，我们可以用共轭解析函数w=f(z)来作为它的复形，且它的共轭导数f'(z)=E正好是该电场的场强.

我们再来看一下共轭解析函数在平面电场中的应用.

例2 研究在点z=0处垂直于z平面的一条无限长均匀电荷线，单位长度所带电荷量为m所激发的静电场.

显然，这是一个调和平面场，只需研究z平面上场的特点即可.我们引进共轭解析函数，由题意可知，Argz=常数，所以所求电场的电力线ln|z|=常数，从而所求电场的等位线|z|=常数.此时，w(z)的共轭导数正好是该电场的场强.

［1］王见定.半解析函数与共轭解析函数［M］.北京:北京工业大学出版社，1988.35－84.

［2］王见定.半解析函数与共轭解析函数及其在力学上的应用［J］.力学进展，1997，27(2):257－263.

［3］仝泽柱，娄正凯.复变函数共轭解析的充要条件［J］.徐州工程学院学报，2006(3):97－106.

［4］王海英.复变函数共轭可微的又一充要条件［J］.吉林师范大学学报(自然科学版)，2008(2):82－83.

［5］彭志刚.一类算子值解析函数族的极值点［J］.数学物理学报，2008，28A(5):945－957.