高超声速飞行器末端导引与控制一体化研究

肖 红 王 勇 国海峰 李望西 唐传林

空军工程大学航空航天工程学院，西安 710038

高超声速飞行器(Hypersonic Vehicle, HV)进入末制导阶段，为了以给定的弹着角精确打击目标，需要一种满足过载约束、受扰动影响小的导引律。最优导引律和滑模导引律都需要对剩余飞行时间进行估算，估算的精度很大程度上制约着导引精度[1]，不易实现。由于HV打击慢移动目标对导引律的要求并不高，比例导引+系数自适应的导引律(APN)有效且易于实现[2]，是合适的选择。由于HV跨大气层飞行时具有复杂的气动特性，气动热导致飞行器结构弹性形变，加之打击精度的高要求，HV控制器的设计变得非常复杂[3-7]。因此，针对HV的导引与控制一体化研究将是HV研究的方向。

针对常规导弹拦截机动目标的问题，文献[8]提出了基于动态逆和状态观测器的制导控制一体化设计，文献[9]提出了基于自抗扰控制的制导与运动控制一体化设计。它们的共同点是将运动方程和姿态控制方程纳入一个控制模型中求解，很好地解决了目标机动带来的制导控制难题。该方法对于打击静止目标的HV没必要，而且HV气动特性复杂，很难实现。本文针对HV打击静止目标的问题，结合APN的特点，克服HV特殊的控制特点，提出了一种新的导引控制一体化设计方法。同时，建立的制导控制一体化模型，它包含了部分制导指令，而不包括HV的运动模型。根据APN所决定的弹道特性，通过分段对一体化控制模型进行了简化，并对各段单独设计了鲁棒控制律。对于一体化控制模型的求解，反演方法能够很好地解决系统的非线性问题，而自适应滑膜控制能够很好地解决系统的参数大扰动问题，本文将二者结合，得到了满意的一体化控制律。最后，通过对导引律的调整，降低控制回路发散的可能性。仿真表明，一体化设计具有较强的系统鲁棒性和高打击精度。

1 末制导阶段问题描述

1.1 坐标系与运动方程

由于末制导阶段航程较短，忽略地球自转，采用目标坐标系，如图1所示。X轴指向东，Y轴指向北，Z轴以竖直向上为正；γ是航迹角，偏上为正；ψ∈[-π，+π]是航向角，顺时针为正；φ∈[0,π/2]是视线角；θ∈[-π,π]是方位角，逆时针为正；V是速度。

由坐标系可知导弹运动学方程为：

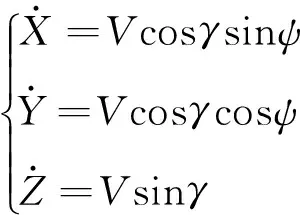
(1)

目标位于原点，要求飞行器以给定的弹着角命中目标，因此终端条件为：γf=Γf,ψf=Ψf,Xf=Yf=Zf=0。

图1 目标坐标系与几何关系

1.2 空气动力模型

本文采用1976年COESA美国扩展标准大气模型，空气密度ρ描述为：

ρ(H)=ρ0×e-(h/H)

(2)

其中，ρ0=1.225kg/m3,H=8.5km。

CLα为升力气动导数，Cl·,Cm·为滚转力矩和俯仰力矩对“·”的气动导数。各个气动导数受高度和HV弹性形变影响剧烈。文献[3，7]对气动参数进行了非线性拟合：

CLα=-8.19×10-2+4.70×10-2M+1.86×10-2α-

4.37×10-4(αM)-9.19×10-3M2-1.52×

10-4α2+5.99×10-7(αM)2+7.74×10-4M3

(3)

由于空间有限，其他气动导数略。

1.3 一体化模型的建立

根据文献[4-6]，采用倾斜转弯的机动方式，忽略侧滑角影响，末制导一体化模型可描述为系统(4)。

(4)

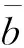
2 导引与控制一体化设计

传统控制模型不包括γ,ψ变量，是为了跟踪导引指令解算出的α,σ，指令γ,ψ到α,σ的生成过程是开环的。由于气动参数的不确定性，这种开环的过渡将造成很大的误差，而且线性的模型无法准确描述非线性耦合HV系统。

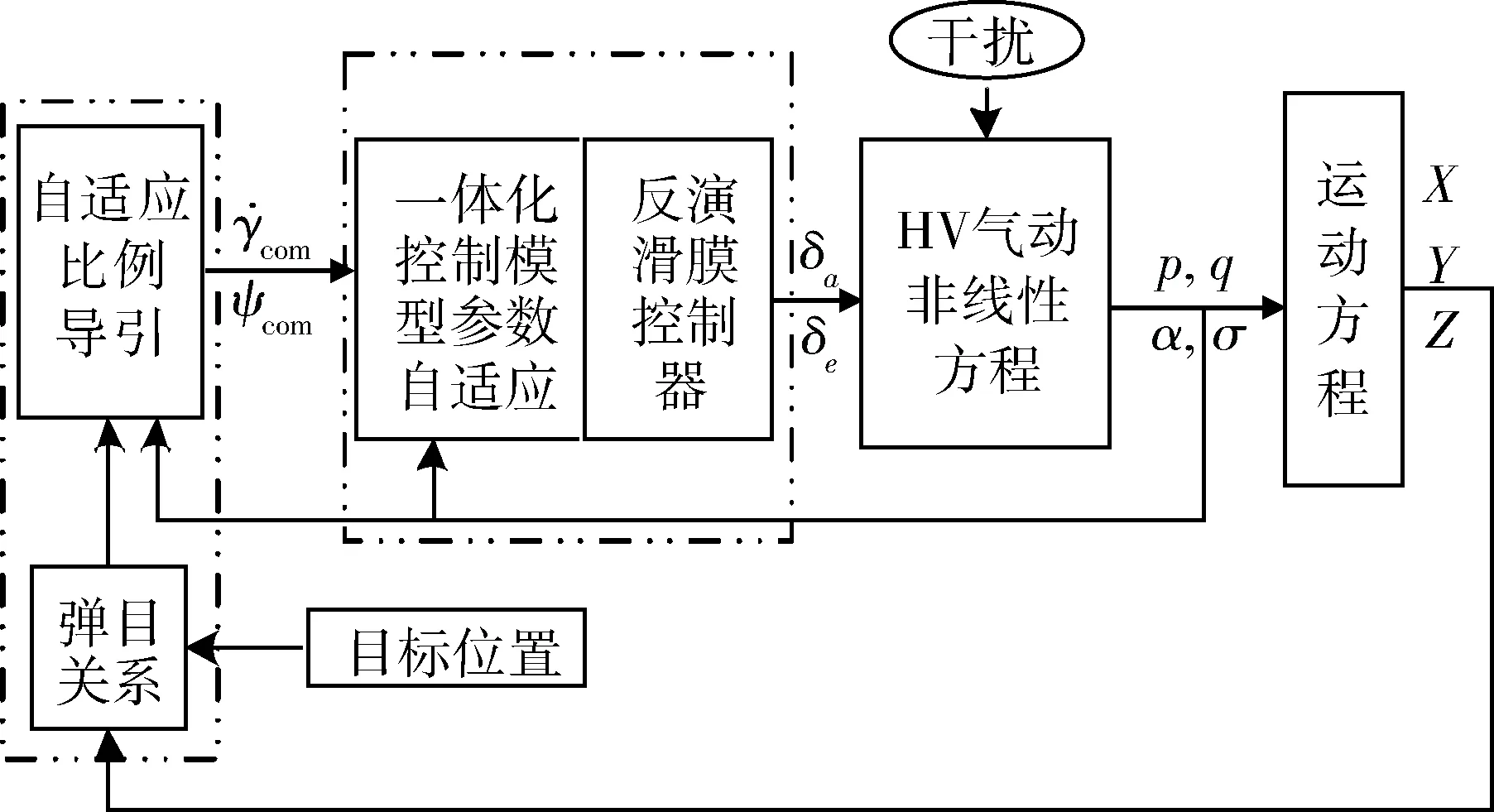
图2 制导控制一体化示意图

2.1 末端导引律分析

本文采用三维比例导引律：

(5)

在要求以给定弹着角打击目标时，飞行器横向瞄准目标之后，才进行纵向瞄准，在横向瞄准之前纵向航迹角保持不变。横向导引律系数选择及更新方法如下[2]：

λ1的选择与更新算法，令：

(6)

(7)

这种设计思路所得导引律必然使得横向瞄准完成前γ保持很小，σ变化很大。横向瞄准完成之后，导弹在纵向以一定的终态航迹角打击目标，此过程σ保持很小，γ变化很大。这些特点可以为控制器的设计提供有用的参考价值。

2.2 自适应Backstepping滑模控制器的设计

设在t0时刻完成横向瞄准，弹道将有下式特点：

|δψ|=|ψt0+θf+π/2|≤ε

(8)

其中ε为任意小正数。如果没有限制横向弹着角，则上面的条件中θf由θ代替。

本文将分两段进行控制器的设计，分割点为横向瞄准完成时刻。设u1,u2分别为分割点前后段控制量，则整个控制器为:

(9)

其中T为过渡时间常量。

2.2.1 控制器设计步骤

在后半段利用sinσ=σ，cosσ=1对系统(4)进行化简。

反演(Backstepping)设计方法的基本思想是将复杂的非线性系统分解成不超过系统阶数的子系统，然后为每个子系统分别设计李雅普诺夫函数和中间虚拟控制量，一直“后退”到整个系统，直到完成整个控制律的设计。

(10)

(11)

定义函数：

其中，k>0，则：

(12)

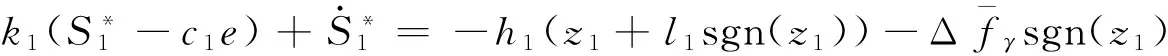
得：

(13)

2.2.2 稳定性分析

将式(12)代入式(11)，得：

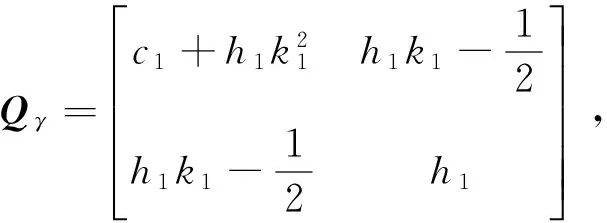
定义函数V(e2)，同理可得：

Fueue+Fδaδa

(14)

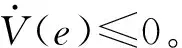
在前半段，γ很小，利用cosγ=1，sinγ=γ简化，可得前半段的控制器函数。

2.2.3 干扰上界自适应估计

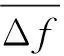
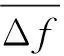
(15)

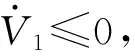
2.3 导引律的改进

由于控制回路的跟踪能力有限，当导引指令长时间超出饱和状态时，控制回路很可能会发散。控制回路的饱和以升力指令超出最大升力为标志。

(16)

(17)

控制回路对导引指令的延迟很大程度上影响最终精度。本文采用比例微分的方式将导引指令相位提前，则最终导引指令为：

(18)

(19)

(20)

(21)

其中w1和w2为指令提前的修正参数。

3 仿真研究

仿真初始条件，目标弹着角以及对应的导引律配置见表1。

表1 初始条件、目标弹着角及导引律配置

加入正弦波干扰(|ΔL|max=0.2L，|Δf|max=0.2f)及飞行器的尺寸参数参照文献[7]的概念机。由于对航向弹着角不作要求，以下仿真只分析航迹弹着角。

图3是HV的整个3D弹道,仿真结果表明，本文方法能够精确打击目标。

图3 导弹3D轨迹图

图4反映了升降舵力矩系数的变化情况。其它力和力矩的系数也是非线性地剧烈变化。仿真结果表明，本文方法能够有效克服系统参数非线性快时变的复杂特性。

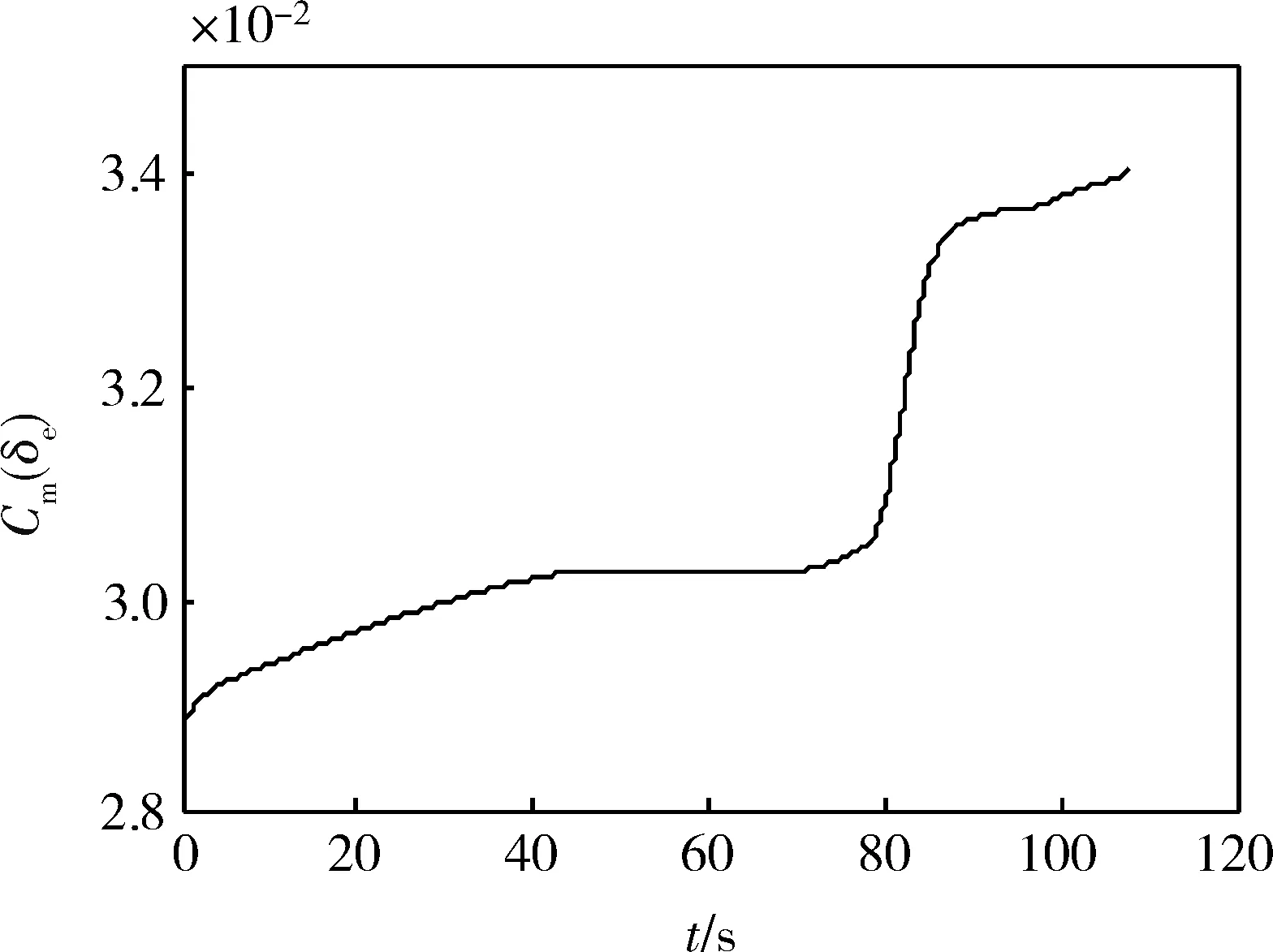
图4 升降舵力矩系数的变化情况

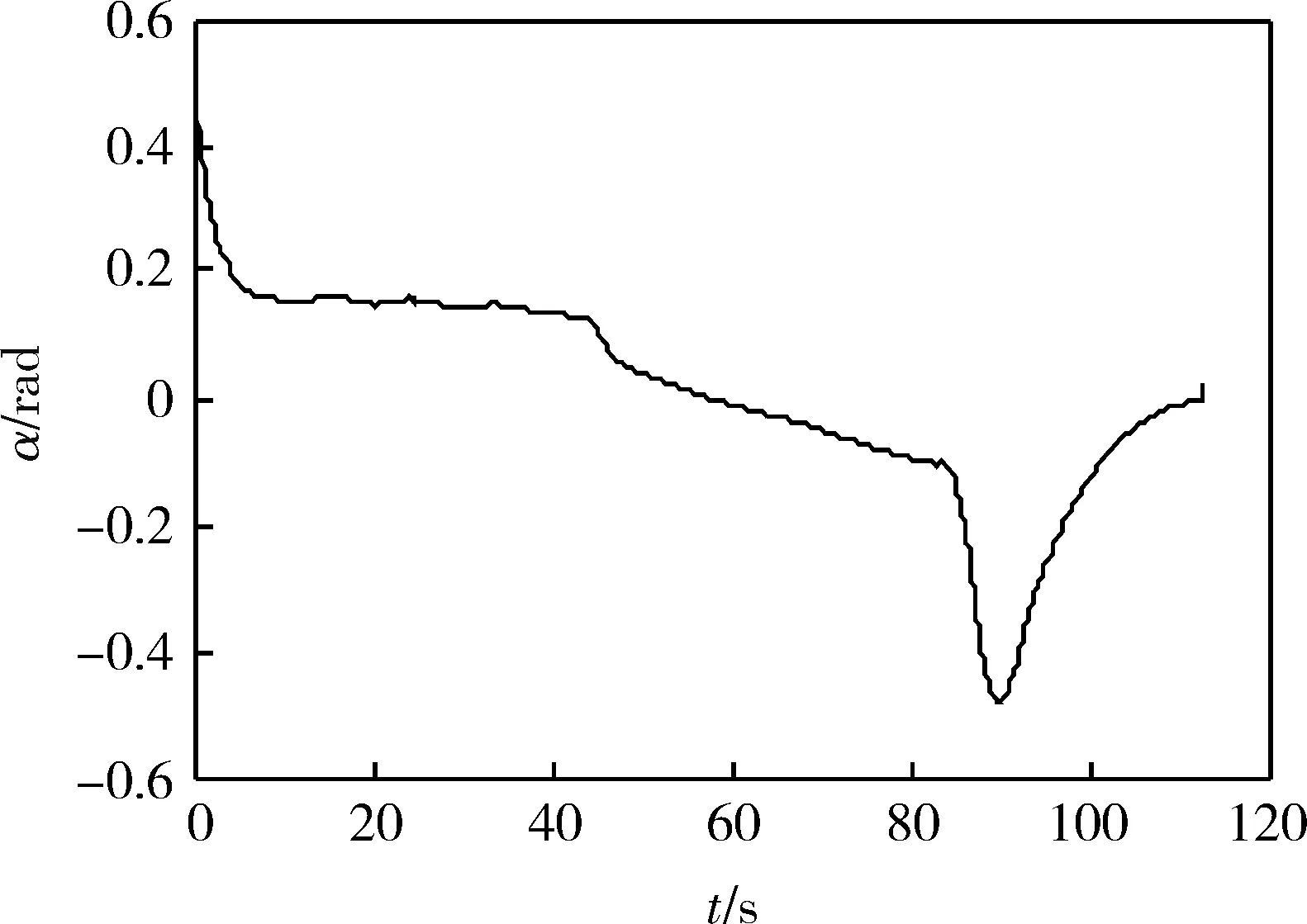
图5 攻角变化

图6 航迹角

图7 航迹角速率指令和实际航迹角速率

比例系数进行了自适应更新(如图8)，比例系数变化范围除在终端时刻附近有较大变化外，其它时刻相对于2变化很小。为了减小高度过小使得系数更新率增大，在导弹与目标还有400m的距离时停止自适应更新，避免更新算法分母项过小。图9是相应的升降舵指令变化情况，最终趋于稳定。

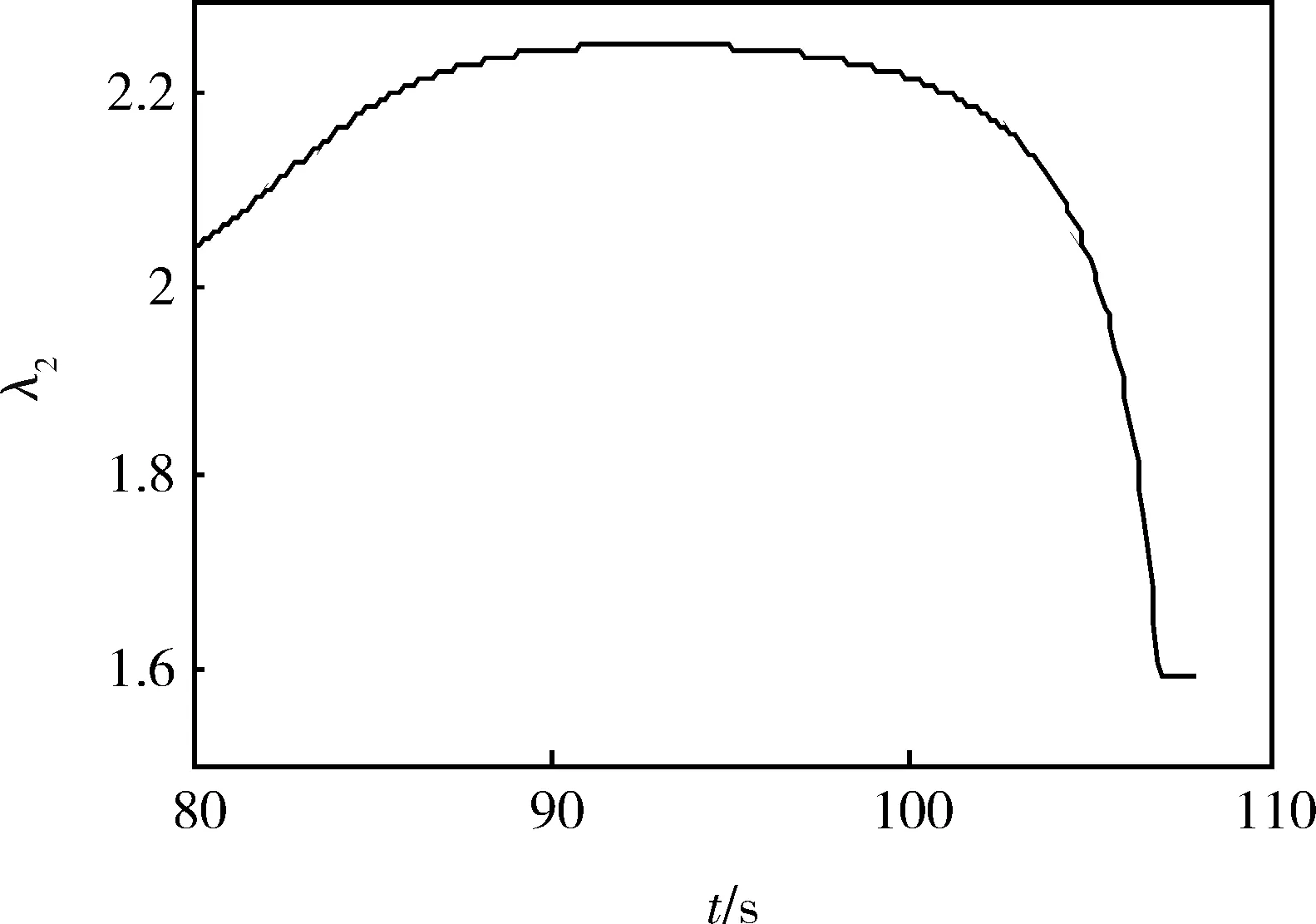
图8 纵向比例系数自适应更新情况

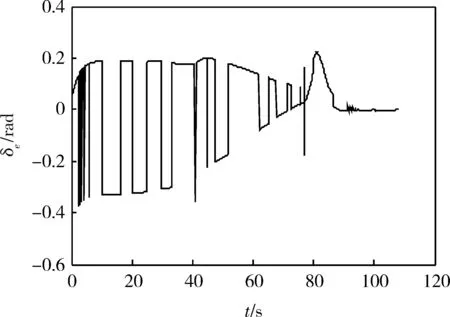
图9 升降舵指令

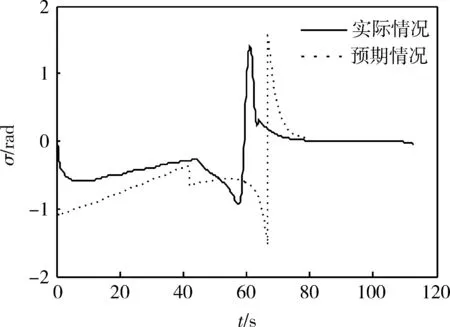
图10 倾侧角

如图11所示，限制副翼的偏转指令大小在0.5rad之内，副翼偏转量在50s附近开始大范围波动，最终趋于稳定。

图6和10验证了导弹运动过程有一个明显转折点的假设，在转折点之前，γ很小，σ变化范围很大；转折点之后，γ变化很大，而σ几乎为0。多次仿真可观察出，转折点以横向瞄准完成时刻为标志，λ2(0)越大，分割点越明显，对应的最大攻角越大。

图11 副翼指令

图11表示了最大攻角|α|max和脱靶量stf及弹着角误差Δγ(tf)的关系。考虑到指令饱和与延迟的方法记为方法1，反之记为方法2。由于不提前修正饱和与延迟，使得控制回路的误差不断积累，最终导致误差很大，甚至控制回路发散。随着最大攻角减小，方法1的误差始终比方法2的误差小。当最大攻角处于中间值时，方法1的效果最明显。当最大攻角过小时，实现精确跟踪是几乎不可能的。

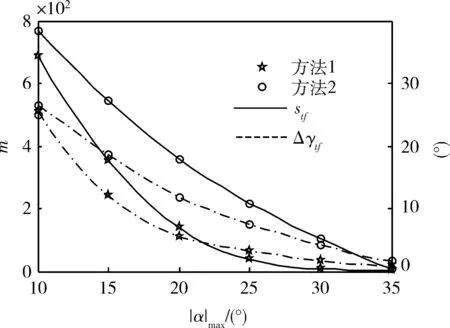
图12 最大攻角与误差

4 结论

针对HV以给定弹着角打击目标的要求，及HV复杂的特性，本文提出了导引与控制一体化的设计思想，并建立了一体化控制模型。结合APN制导律的特点，对一体化控制模型分2段进行了简化。在此基础上设计出了对参数不确定性具有鲁棒性的自适应Backstepping滑模控制器，有效解决了系统的非线性与耦合性问题。在对控制律考察后，相应地改进了制导律，进而增强了系统的稳定性。本文的一体化设计方法，实现了导引和控制的有机结合，有效可行，提高了系统整体性能。

参 考 文 献

[1] 朱凯,齐乃明.基于滑膜干扰观测器的垂直攻击制导律研究[J].兵工学报,2011,32(12):1462-1467.(ZHU Kai,QI Naiming.Research on Vertical Terminal Guidance Law Based on Sliding Mode Disturbance Observer[J].Acta Armamentarii,2011,31(12):1462-1467.)

[2] Lu P, Doman D B, Schierman J D.Adaptive Terminal

Guidance for Hypervelocity Impact in Specified Direction[C]//AIAA Guidance, Navi-gation, and Control Conference and Exhibit,San Francisco: AIAA, 2005: 2108-2129.

[3] Keshmiri S,Colgren R,Mirmirami M.Development of an Aerodynamic Database for a Generic Hypersonic Air Vehicle[C]//AIAA Guidance, Navigation and Control Conference and Exhibit, 2005:1-21,AIAA 2005-6257.

[4] Jeffrey J.Dickeson, Armando A.Rodriguez, Srikanth Sridharan.Elevator Sizing, Placement, and Control-Relevant Tradeoffs for Hypersonic Vehicles[C].AIAA Guidance, Navigation, and Control Conference2-5 August 2010, Toronto, Ontario Canada:AIAA,2010:2010-8339.

[5] 张红梅,张国山.高超声速飞行器的建模与控制[D].天津:天津大学, 2011.

[6] 李海军，黄显林.再入机动弹头的建模与控制[D].哈尔滨: 哈尔滨工业大学, 2010.

[7] Richard Colgren, Shahriar Keshmiri.Nonlinear Ten-Degree-of-Freedom Dynamics Model of a Generic Hypersonic Vehicle[J].Journal of Aircraft, 2009, 46(3):800-813.

[8] 尹永鑫,石文，杨明,等.基于动态逆和状态观测的制导控制一体化设计[J].系统工程与电子技术,2011,33(6):1342-1345.(YIN Yongxin, SHI Wen, YANG Ming.Integrated Guidance and Control Based on Dynamic Inverse and Extended State Observer Method[J].System Engineering and Electronics, 2011,33(6):1342-1345.)

[9] 赵春哲.基于自抗扰控制的制导与运动控制一体化设计[J].系统科学与数学,2010,30(6): 742-751.(ZHAO Chunzhe.Adrc Based Integrated Guidance and Control Scheme[J].Journal of Systems Science and Mathematical Sciences, 2010,30(6):742-751.)

[10] 高为炳.变结构控制的理论及设计方法[M].北京:科学出版社,1999.