捷联惯导方位大失准角对准研究

赵鹏飞 齐建宇

1.北京航天自动控制研究所，北京 100854 2.宇航智能控制技术国家级重点实验室，北京 100854

捷联惯导系统(SINS)初始对准的目的是为了获得载体坐标系相对于导航坐标系的坐标变换矩阵，即姿态矩阵，对准精度直接影响惯导系统的导航精度。SINS初始对准通常可分为粗对准和精对准2个阶段。在粗对准阶段，利用地球自转角速度和重力加速度作为参考量，利用加速度计及陀螺仪的输出求取粗略的姿态矩阵；在精对准阶段，建立导航计算坐标系和真实导航坐标系间的失准角模型，通过卡尔曼滤波估计出失准角，从而获得准确的姿态矩阵。

经典的基于Φ角法或ψ角法推导的误差模型是在小失准角条件下获得的，利用Kalman滤波最优估计能有效解决小失准角条件下的SINS初始对准问题[1]。文献[2-3]研究了方位大失准角对准误差模型。建立大失准角模型的主要目的是为了在方位角未知的情况下使模型更符合实际。当系统加电启动后，若方位角信息未知，方位失准角不是小量时，系统模型是非线性的，因此失准角为小量时的线性误差方程不能表示大失准角时的误差传播特性。本文在游动方位角坐标系下推导了SINS的方位大失准角误差模型，并在静基座和动基座下分别对模型进行了验证，结果表明误差模型在方位大失准角情况下是有效的。

1 SINS方位大失准角误差模型

记地心惯性系为i系，地球坐标系为e系，机体坐标系为b系，导航坐标系为n系。由n系依次经过3次欧拉角ψG,θ,γ转动到b系。

1.1 导航方程

文中导航坐标系采用游动方位角坐标系，真实方位角ψ与游动方位角a的关系为ψ=ψG-a。SINS导航方程主要由速度更新、位置更新和姿态更新方程组成。位置矩阵满足以下微分方程：

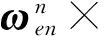
速度微分方程为

姿态矩阵微分方程为

1.2 方位大失准角误差模型

为避免误差模型的非线性问题，方位大失准角误差模型公式常用2个方位角误差变量来表示，例如δsin(a)和δcos(a)[2]或者δsin(ψ)和δ[1-cos(ψ)][4]。关于这2种不同的方位角误差变量设置的对比可在参考文献[5]中查到。以上2种模型都适用于静基座对准，可以通过KF算法进行对准滤波，系泊状态下的对准也可以使用上述模型。另外，也可直接用游动方位角误差δα作为状态变量，通过EKF进行对准滤波。本文的推导使用δα作为状态变量。

1.2.1 速度误差方程

当不考虑任何误差时，速度的理想值由下式确定：

(1)

实际含误差的导航解算微分方程为

(2)

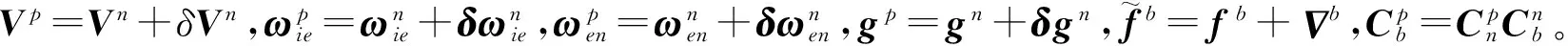
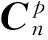
其中“s”和“c”表示sin和cos函数(下同)，令

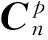
由加速度计测量，有

(3)

由式(3)得

(4)

式(2)减去式(1)，并将式(4)带入，忽略δgn的影响，并略去二阶小量，得SINS速度误差方程，

(5)

上述误差分析中，利用到

其中，h表示惯导高度，Rx和Ry表示沿导航坐标系x和y方向的曲率半径，满足

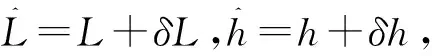
注意到式(5)不同于文献[3]中另一种速度误差方程的形式：

(6)

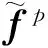
1.2.2 姿态误差方程

引入向量

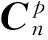
(7)

(8)

(9)

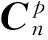
(10)

由式(7)和(8)可得：

对应向量方程为

(11)

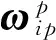
(12)

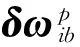
上式可写成

(13)

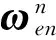
为了避免非线性问题，在精对准过程中可对游动方位角的正弦函数和余弦函数的误差进行建模，状态向量采用δsa和δca，系统误差模型可用线性KF进行滤波。而当进行动基座对准时，则需要使用EKF非线性模型滤波方法。

另外，位置误差方程的推导过程中不需要对姿态误差角作小角度假设，将文献[2]中给出的位置微分方程的诸量用理论值与误差量之和代替，即得适用于大失准角的位置误差方程。

1.2.3 SINS初始对准滤波模型

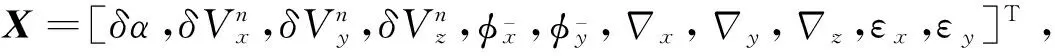
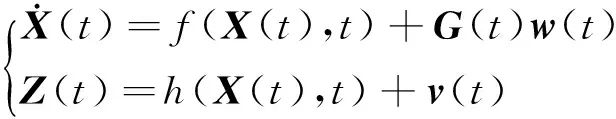
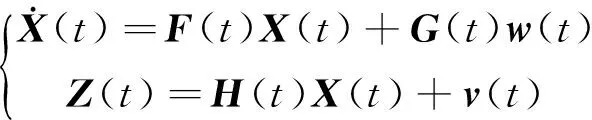
(14)

其中F(t)为f(X(t),t)的雅可比矩阵，H(t)为h(X(t),t)的雅可比矩阵。

对式(14)作离散化处理，设采样周期为T，离散化后的状态方程和量测方程为

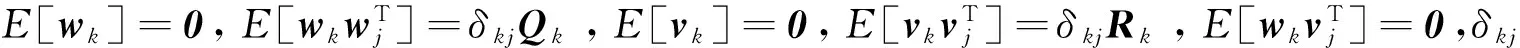
当T为小量时，

仿照线性卡尔曼滤波基本方程，可写出扩展卡尔曼滤波递推公式为

2 仿真

进行了静基座初始对准计算，计算数据来源于真实惯导系统输出。其中粗对准采用解析法粗对准[6]。精对准使用上文推导的模型进行EKF滤波，对准过程姿态角变化曲线如图1所示。图1说明利用方位大失准角模型滤波适用于小失准角的情形。

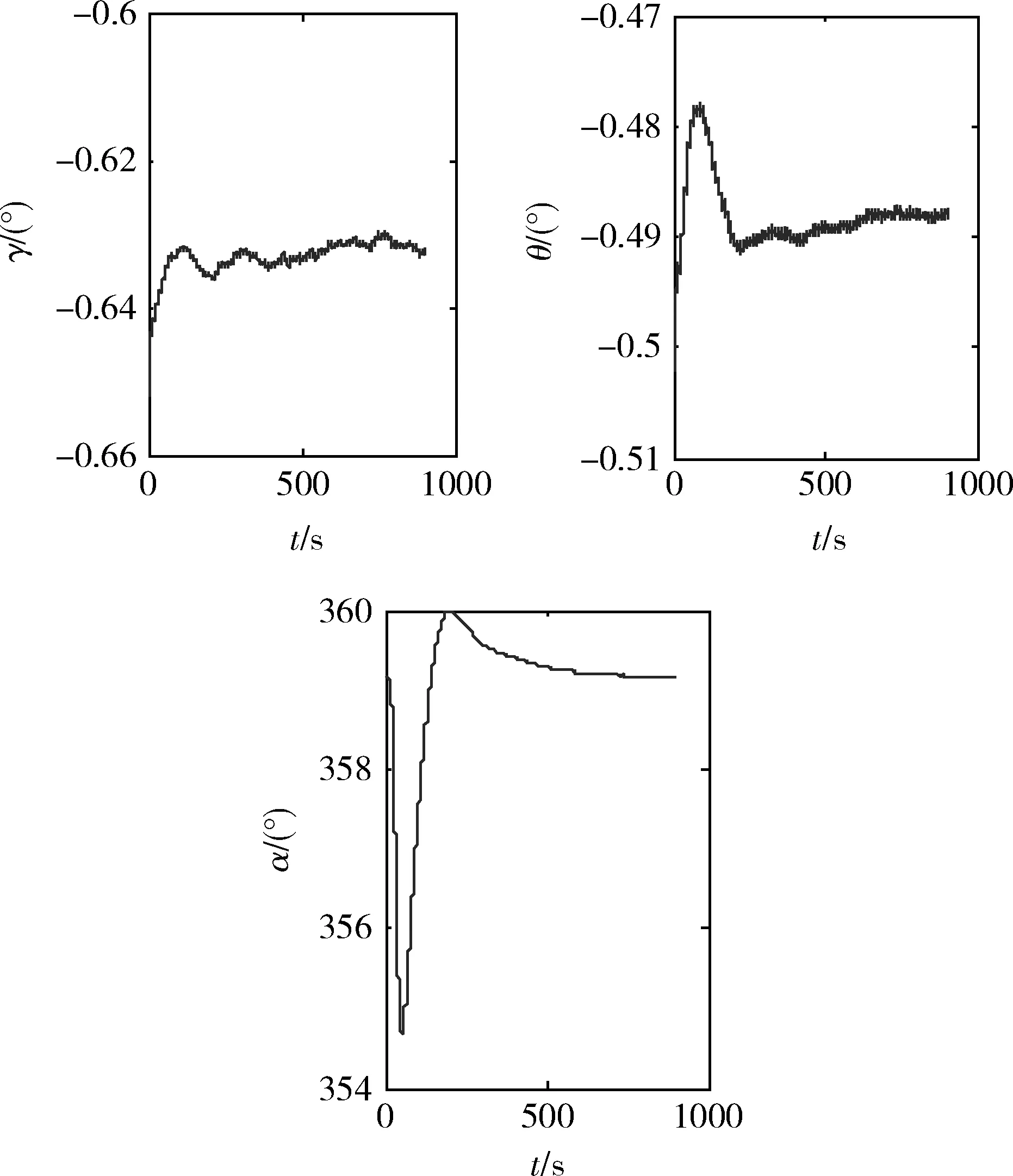
图1 静基座精对准姿态角变化

在上述粗对准结果中将方位角加入1个失准角-175°，对准过程姿态角变化曲线如图2所示，可见该模型能迅速修正大方位失准角。

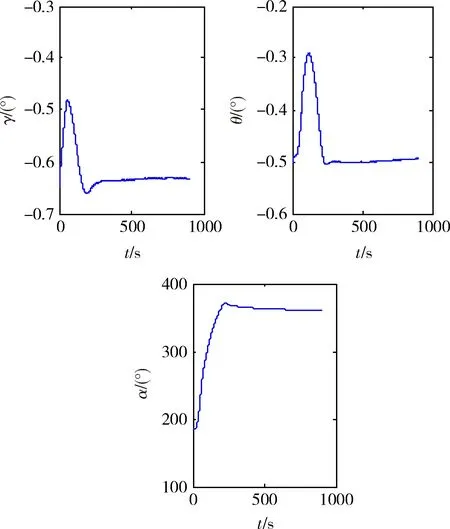
图2 方位大失准角情形

进一步分析失准角分别为-65°,-125°,-175°时方位角的收敛情况，可以看出初始失准角越大，滤波收敛时间越长。因此，在初始方位角误差较大时，采用反馈修正的方法不断减小失准角误差，对初始对准是有益的。当失准角降低至比较小时，滤波模型可由方位大失准角模型转为使用小失准角线性模型，从而降低计算量。

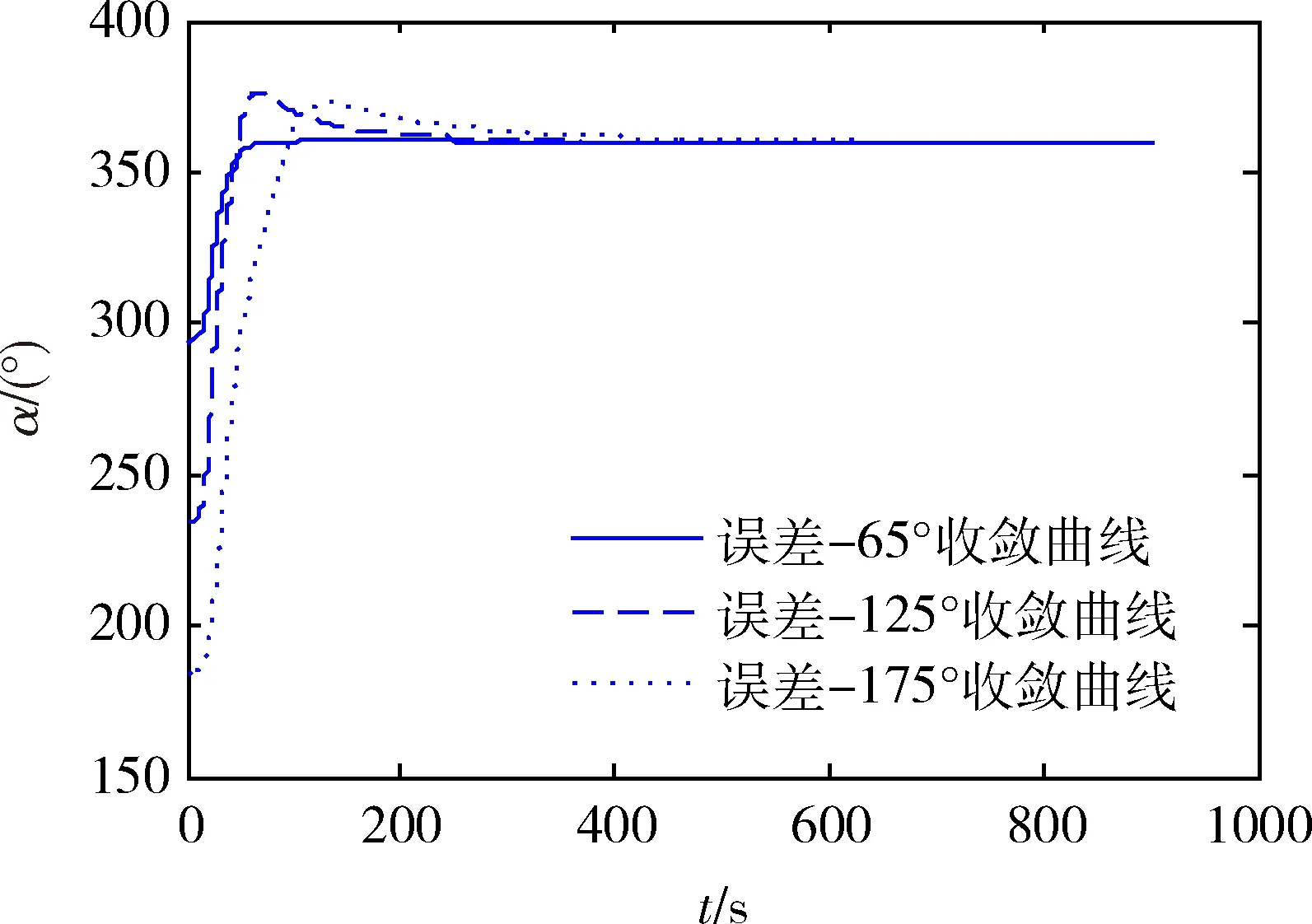
图3 不同失准角情况的收敛曲线

表1给出了方位失准角为-65°时，EKF滤波稳定后(对准结束前30s内)姿态误差的估计均值，表中还给出了使用δsa和δca模型处理同样数据的KF对准精度。对于静基座对准，采用δsa和δca线性模型能够获得和采用非线性误差方程同样的精度。

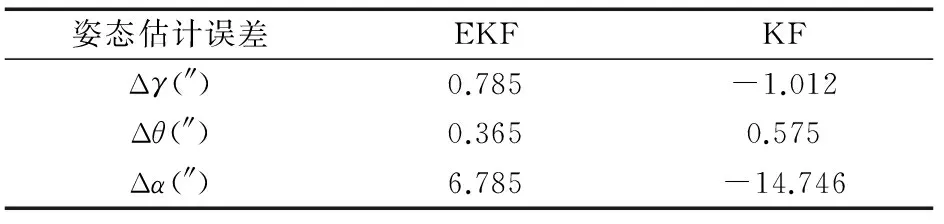
表1 静基座对准精度比较

本文推导的模型同样适用于动基座下的初始对准。采用相同的惯组在运动状态下的数据进行初始对准。对准开始首先假设初始姿态角均为0°，建立初始姿态矩阵。实际对准情况为水平姿态角在0°附近，方位失准角未知，符合模型假设。使用本文建立的模型进行Kalman滤波，用反馈校正，初始对准时间870s。姿态角误差曲线如图4所示，可见水平失准角收敛较快，方位失准角收敛较慢。

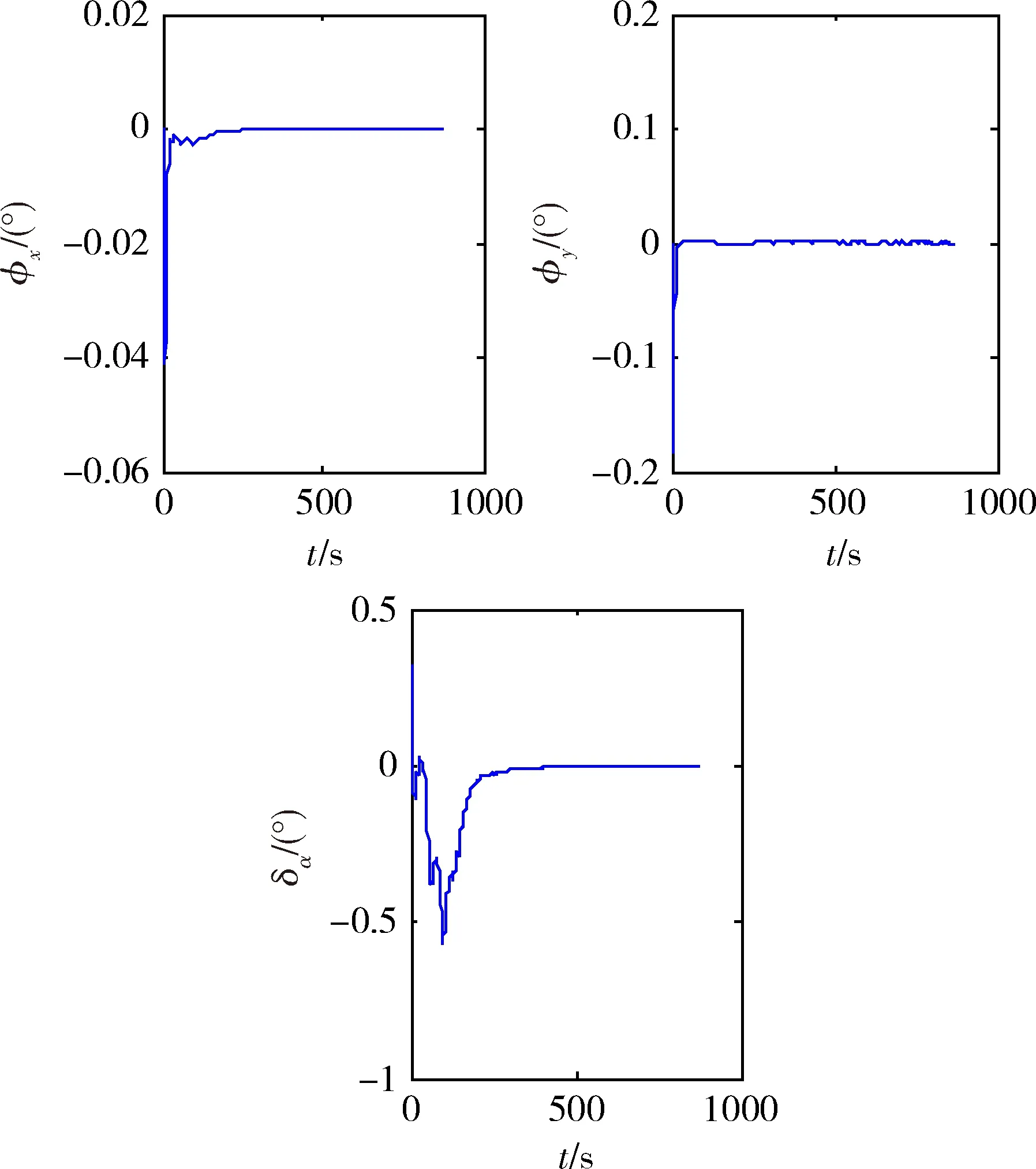
图4 姿态角误差曲线

3 结论

本文讨论了捷联惯导系统在方位大失准角下的对准问题。当姿态误差角不能被看作小角度时，采用经典的Φ角法或ψ角法推导的误差模型将会带来很大的模型误差。在游动方位角坐标系下推导了方位大失准角条件下的SINS初始对准误差模型，给出了游动方位角坐标系下误差模型的表达式。

对SINS在方位大失准角下的静基座和动基座初始对准进行了试验研究，结果表明所提出的SINS非线性误差模型可有效滤除大方位失准角。方位失准角越大，滤波收敛所需的时间就越长，可通过反馈修正的方法减小方位失准角。

参 考 文 献

[1] 秦永元, 张洪钺, 汪叔华.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社,1998.

[2] Pham T M.Kalman Filter Mechanization for INS Airstart[J]. IEEE AES Systems,Jan.1992.

[3] Dmitriyev S P.Nonlinear Filtering Methods Application in INS Alignment[C]. IEEE Transaction on Aerospace and Electronic Systems, Jan. 1997.

[4] Scherzinger B M. Inertial Navigation Error Models for Large Heading Uncertainty[C]. IEEE Position Location and Navigation Symposium, 1996.

[5] Rogers R M. Large Azimuth INS Error Models for In-Motion Alignment[C]. ION National Technical Meeting Paper, 2001.

[6] 陈哲.捷联惯导系统原理[M].北京：宇航出版社,1986:128-132.