矩阵特征值与特征向量的又一种求法
2013-05-14魏裕博
魏裕博
(陕西学前师范学院数学系, 陕西西安 710100)
大多数代数教材中,对于求一个n阶矩阵A的特征值与特征向量,所讲授的方法是通过求解矩阵A的特征方程|λE-A|=0与相应的齐次线性方程组(λiE-A)X=0来实现的。这里给出了利用矩阵多项式和种子向量来求解的另一种方法。
命题1A是一个n阶矩阵,u∈Rn且u≠0,设k是使u,Au,A2u,…Aku线性相关的最小正整数,则存在k次实系数多项式f(x),若λ0是其一个根,那么f(x)=(x-λ0)q(x),这时q(A)u就是矩阵A的属于特征值λ0的特征向量。(u称为种子向量,Au,A2u,…Aku称为由u生成的向量)。
证明:∵k是使u,Au,A2u,…Aku线性相关的最小正整数,
∴ 存在不全为零的数a0,a1, … ,ak∈R, 使a0u+a1Au+…+akAku=0.
(1)
令f(x)=a0+a1x+…+akxk(由k的最小性,ak≠0) ,
(2)
若λ0是f(x)的一个根,则存在k-1次多项式q(x), 满足f(x)=(x-λ0)q(x)
将矩阵A代入上式,且由(1)式可得
f(A)u=(A-λ0E)q(A)u=0,
即
A(q(A)u)=λ0(q(A)u
由k的最小性,q(A)u≠0,因此q(A)u是A的属于特征值λ0的一个特征向量。


令f(x)=x-2,则2是其一个根。则f(A)u=(A-2E)u=0,
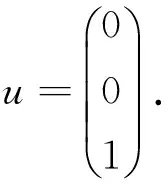
由例1看到,取不同的种子向量可能得到矩阵A的不同特征值和特征向量,那么取定第一个种子向量后,如何取第二个、第三个以求得其它的特征值和特征向量呢?

证明: 由题设u,Au,A2u,…Ak-1u,v,Av,…,Al-1v,Alv线性相关,则存在关系式


(1)
由命题(1)知f(A)u=0,故用f(A)左乘(1)式,得
f(A)(b0E+b1A+ …+blAl)v=0
(2)

将A代入,并由(2)式得 (A-λ0'E)f(A)p(A)v=0

命题2 给出了用第二个种子向量求新的特征值和特征向量的方法,需要的话可以取第三个、第四个种子向量,这个过程继续下去,直到求得A的所有特征向量的一个极大线性无关组为止,同时也求得了A的所有不同的特征值。
例2 求例1中其它特征值与特征向量
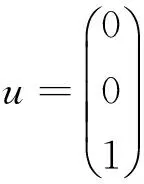
知u,v,Av,A2v线性相关,且A2v-2Av+v+0u=0,
令g(x)=x2-2x+1,则x=1是其二重根,且g(A)=(A-E)2
而f(A)(A-E)v≠0,即(A-2E)(A-E)v=(2,4,-2)T≠0,
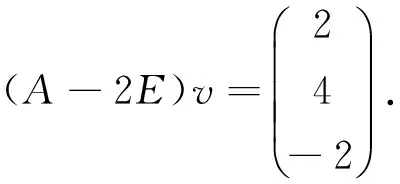

以上例子中,特征值、特征向量均为实值。其实,一个实矩阵可能会出现复的特征值,相应就有复的特征向量。那么一个实矩阵的复特征值与复特征向量有什么特点呢?
命题3 若实矩阵A有复特征值,则它们必然共轭成对出现,且属于共轭的复特征值的复特征向量也相互共轭。
证明:设λ是A的一个复特征值,α是属于λ的特征向量,则有
Aα=λα



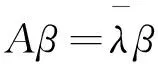
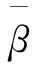

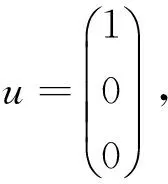
故有B3u-B2u+Bu-u=0.
(1)
设f(x)=x3-x2+x-1 , 则在复数域范围有
f(x)=(x-1)(x2+1)=(x-1)(x-i)(x+i)
即f(x)有一个实根λ1=1和一对共轭复根λ2、3=±i.
将B代入,并由(1)得 (B-E)(B-iE)(B+iE)u=0
由此可得,B的属于λ1=1的一个特征向量
B的属于λ2=i的特征向量为

B的属于λ3=-i的特征向量为
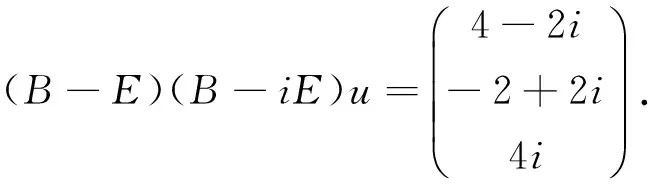
用矩阵的多项式和种子向量,无需计算行列式和求解一系列的齐次线性方程组,就可直接求得矩阵的特征根和特征向量,但必须对矩阵运算及向量线性相关性的判断熟练掌握。
[参 考 文 献]
[1] 邱森.线性代数探究性课题精编[M]. 武昌:武汉大学出版社,2011.
[2] 邱森,朱林生.高等代数探究性课题集[M]. 武昌:武汉大学出版社,2008.
[3] 陈怀琛,高淑萍,杨威. 工程线性代数[M]. MATLAB版.北京:电子工业出版社,2011.
[4] 天津大学数学系代数教研组.线性代数及其应用[M].北京:科学出版社2010.
[5] 李林曙,施光燕.线性代数[M].北京:中央广播电视大学出版社,2002.
[6] 西北工业大学应用数学线性代数教学组.线性代数[M] .3版.西安:西北工业大学出版社,2006.
