NBTI界面电荷反馈引起器件寿命变化的数值分析
2013-05-12曹建民黄思文张旭琳
曹建民,贺 威,黄思文,张旭琳
深圳大学电子科学与技术学院,深圳 518060
NBTI界面电荷反馈引起器件寿命变化的数值分析
曹建民,贺 威,黄思文,张旭琳
深圳大学电子科学与技术学院,深圳 518060
提出一种用二维器件数值模拟和负偏压温度不稳定性 (negative bias temperature instability,NBTI)模型联合计算的方法,分析NBTI效应产生的界面电荷对pMOS器件栅氧化层电场和沟道空穴浓度的反馈作用.通过大量计算和比对分析现有实验得出:当NBTI效应产生较多的界面电荷时,由于界面电荷反馈,pMOS器件的NBTI退化将有一定程度的减小.这种退化减小是一种新的退化饱和机制,对不同类型器件的寿命具有不同的影响.在低NBTI器件中,界面反馈对器件寿命曲线的变化影响不大,器件寿命曲线趋向满足指数变化规律.在高NBTI器件中,界面反馈使得寿命曲线变化基本满足幂指数变化规律.
半导体技术;MOS器件;负偏压温度不稳定性;计算机辅助设计;界面反馈;半导体器件寿命
随着超大规模集成电路的发展,负偏压温度不稳定性(negative bias temperature instability,NBTI)效应引发的pMOS器件退化已成为影响电路寿命的主因[1].NBTI效应的退化与应力时间t普遍存在幂指数关系tn,实验显示,n约为1/6[2-3],传统的反应扩散R-D模型 (reaction-diffusion model)能很好地解释该退化关系.然而,当应力时间继续加长,时间幂指数n会逐渐减小,趋于饱和[3-5].这对半导体工业来说是利好,因为应力退化饱和意味着器件寿命的延长,使得该现象倍受重视并已有多种模型来解释这种饱和[4].其中最常见的有两种:一种称硬饱和[5],是因为界面电荷的产生接近于界面处存在的Si—H键的数量时出现的饱和现象;另一种称软饱和[4],是因为H2分子在多晶硅和在栅氧化层中的扩散系数不同而引起.然而,这些模型都和大部分的实验现象不符[3],NBTI的退化饱和现象物理机制主要是什么仍是疑问.
R-D模型假设界面电荷的产生是引起NBTI退化的主要原因.反应生成的界面电荷会引起栅氧化层电场的变化;栅氧化层电场的变化又会引起界面电荷的变化,显然在器件栅氧化层/硅界面存在着界面电荷引起的反馈作用[6-7].对这种反馈作用目前尚无文献分析报道.本研究基于传统R-D模型,考虑器件沟道空穴浓度和栅氧化层电场对R-D模型的影响,将其和半导体器件数值模拟软件TCAD结合进行联合求解,研究栅氧化层/硅界面的这种界面反馈作用和退化饱和,以期分析器件寿命变化的物理机制.
1 R-D模型
本研究在分析过程中需对R-D模型和器件数值模拟方法进行设定和修改.传统的R-D模型是用于描述栅氧化层/硅界面电荷的产生和界面处氢物质扩散的方程组.假设在pMOS器件栅氧化层/硅界面处存在大量不稳定的Si—H键,当给器件施加适当的负栅压,即器件处于反型状态时,这些Si—H键可能被打破 (打破的Si—H键等同于界面电荷的产生),生成H原子 (或H2分子),并沿栅极方向做扩散运动,从而决定了栅氧化层/硅界面电荷的产生数量,也决定了器件参数的NBTI漂移退化.
在直流应力作用下,考虑H2分子的扩散,R-D模型的解析解为[7-8]

其中,Nit为界面电荷产生的数量,也是Si—H键的断裂数量;Eox为栅氧化层电场强度;p为器件沟道表面的空穴浓度;β为电场引起退化的加速因子;t为应力时间;ARD为依赖材料类型的常数,其值越大,说明越容易产生界面电荷,反之亦然.

其中,N0为界面处Si—H键的数量;kf0为Si—H键断裂的基础速率;kr为Si—H键复合的速率;kH为H原子结合成H2分子的结合率常数;Dp为H2分子在多晶硅中的扩散系数.
由界面电荷引起器件阈值电压的漂移退化为

其中,q是电荷电量;Tox是氧化层厚度;εox和ε0分别是二氧化硅和真空的介电常数.
阈值电压的漂移式(3)中未考虑空穴俘获(hole-trapping)的影响,主要是因为在纯SiO2栅和薄SiON栅中,NBTI退化主因是界面电荷的产生[7],因此本研究具有一定的普适性.
2 联合模拟方法
为分析界面电荷的反馈作用,需结合R-D模型解析解(1)和半导体器件数值模拟软件,进行联合求解.该联合数值模拟的软件流程图如图1.
1)由器件模拟软件设置一定偏置电压Vg和应力时间t=tstart.在Genius-Open软件中设置界面电荷Nit=0、并计算出pMOS器件的稳态值.按照NBTI效应的定义,此时源漏电压Vds=0.
2)从硅层内取出界面的空穴浓度p和从栅氧化层内取出Eox的值,分别记为pold和Eox_old,代入如式(1)的R-D模型计得界面电荷Nit(t).按照R-D模型理论,断裂的Si—H键如同界面电荷的产生,而且界面电荷的产生是由扩散控制的,界面电荷产生的过程也处于稳态.
3)将Nit(t)作为器件中的界面电荷,代入Genius-Open软件计算新的稳态值,此时将会产生新的p和Eox,分别记为pnew和Eox_new.
4)用Eox(或 p)作为比较参数,当 Eox_new与Eox_old的绝对差值,大于限定误差ε时(或以p为参数,pnew与pold的绝对差值大于限定误差),重新计算Nit(t),并计算器件稳态,循环至满足小于限定误差的条件.

图1 半导体器件模拟软件 (Genius-Open)和R-D模型联合模拟流程图Fig.1 Flow chart of the joint calculation of semiconductor device simulation(Genius-Open)and the R-D model
5)当Eox_new与Eox_old的差值小于限定误差ε时,认为界面电荷反馈不存在,存储此时的Nit(t),并返回继续计算下一个应力时间t的Nit(t).
6)当达到一定的应力时间tstop,时间循环结束,输出文件为记录各时刻Nit(t)值的集合.
最后输出的各时刻界面电荷Nit(t)集合,反映了一定时间内的、带反馈作用的界面电荷,与利用式(1)直接计算的Nit(t)(未考虑反馈作用)比较,就能看出界面电荷反馈的大小.还可利用式(3)计得阈值电压漂移ΔVt(t),与实验数据比较,能验证这种反馈作用发生的条件.
由于典型的NBTI效应发生在器件源极和漏极电压为0,栅压为负,器件处于反型状态时 (稳态),器件模拟计算稳态相对成熟,所以可采用通用的器件模拟软件来计算.然而,要从计算结果中准确快速地提取空穴浓度p和栅氧化层电场Eox,且对界面电荷Nit进行大量的计算,并要计算其反馈作用,就需自行编制软件,将R-D模型解析解数值化,使以上几部分的计算能联合进行.传统的半导体求解商业软件 (如MIDICE等)并不支持此功能,这是目前NBTI退化机理研究遇到的瓶颈之一.Entner等[6]曾首次将R-D模型和半导体器件方程组联合求解,但仅报道了NBTI效应中恢复效应的模拟结果,器件界面反馈数值模拟分析尚未见报道.
鉴于Genius-Open软件[9]源代码具有完全开放性,本研究采用该软件编制退化模型完成以上任务.值得注意的是,Genius-Open软件虽然拥有完善的能量平衡模型,适用于模拟沟道长度为0.1~1.0 μm的MOS器件 (深亚微米器件),但是其量子修正模型尚不完善,当器件沟道长度小于0.1 μm,栅氧后厚度小于2 nm,器件的数值模拟必须考虑量子效应[8,10],因此本研究的器件模拟只局限于深亚微米,未考虑量子效应.
3 模拟结果与讨论
pMOS器件模型参数选取为:栅氧厚度Tox=2.2 nm;器件宽比 W/L=10 μm/0.12 μm;沟道掺杂浓度为 Nd=5 ×1017cm-3,和 Reisinger H[11]实验测试的器件参数相近,便于比对.以下讨论若无特别说明,器件模型都采用以上参数.
3.1 低NBTI器件的退化
为与实验数据比较,R-D 模型参数[7-8,12]设为:kf0=6.11 ×10-22cm3/s;kr=3 ×10-9cm3/s;N0=5×1013cm-2;Dp=2.57 ×10-15cm2/s;kH=5.37 ×10-6cm3;β=0.52 cm/MV.其中,界面处 Si—H键的数量N0取值较高,是为了避免“硬饱和”[5]对界面反馈的影响.按照以上参数可计算材料常数ARD=3.4×10-4s-1/6,为相对较小的常数,因此该器件属于低NBTI效应的器件.分别模拟该器件阈值电压漂移ΔVt随应力时间t的变化结果,如图2.
当栅极电压在-2.2~-2.8 V范围变化时,数值模拟得到的ΔVt的变化能很好地反映实验数据的变化趋势[11],退化的时间幂指数n都约为1/6,说明本研究提出的R-D模型选取的材料参数ARD是合理的.然而,仔细观察模拟得到的时间幂指数发现,当 Vg=-2.2 V 时,n=0.165 8;当 Vg=-2.8 V时,n=0.164 9,有变小趋势 (退化饱和).我们认为这种变化是由于界面反馈形成的,只是在这个栅极电压变化的范围内,幂指数变化不明显,实验很难测试出此变化.仅当栅极电压的绝对值大于3.2 V后,才能观察到明显的界面反馈作用.对应100 mV的阈值电压退化,可反推出界面电荷约为1012cm-2,即在低NBTI器件中,当界面电荷数Nit>1012cm-2时,才可观察到明显的退化饱和现象.

图2 ARD=3.4×10-4s-1/6时,器件有反馈和无反馈的ΔVt(线段)随时间t退化特性,以及与实验数据[11](点)比较Fig.2 ΔVt(line)versus t characteristics of NBTI degradation with and without the interface feedback,and compared with the experimental trends[11] (point)for ARD=3.4×10-4s-1/6
从形态上看,界面反馈引起的这种退化饱和类似于硬饱和[5],都是发生在较长应力时间和界面电荷产生达到较大的数量时,且在同样的界面电荷(阈值漂移)时,不同栅压曲线出现的饱和几乎相同.但两者也有本质区别,界面反馈引起的饱和是因为界面电荷较大而引起的,与界面处存在的Si—H键数量关系不大.由此可见,这是一种新的退化饱和机理,可用于器件和电路的寿命研究.
3.2 低NBTI器件的寿命
将图2中器件阈值电压退化数据,以失效标准(failure criterion,FC)=80 mV(器件的阈值电压为0.7 V,80 mV的退化程度为11.4%),取对应器件的退化时间作为寿命,做出寿命随栅压/电场的变化如图3.
图3寿命曲线能很好地体现器件阈值电压漂移随栅电压的变化的加速过程.栅压越大,器件寿命越小.以栅压较大 (Vg取值-2.8~-3.4 V)的寿命点作为基准,分别以指数规律和幂指数规律外延出低栅压时的寿命数据发现,模拟出的寿命数据,介于指数和幂指数变化之间.当Vg取值-1.7 V(Eox=5 MV/cm)时,幂指数外延高估36.3倍的寿命;指数外延低估了3.6倍的寿命.这是由于式(1)的电场加速退化模型决定的,空穴浓度p和栅氧化层电场Eox都在一定程度上决定了寿命的曲线变化,此结论与文献[7]等一致.
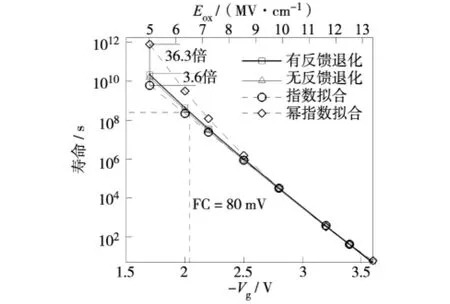
图3 低NBTI器件的寿命随栅压的变化.Fig.3 Eoxand-Vgdependence of lifetime in the low NBTI device
对于本研究选择的低NBTI器件,其寿命曲线更趋于满足指数关系.当器件寿命为5 a(1.6×108s)时,其工作电压达2 V.当栅压大于2 V变化时,器件寿命变化曲线基本满足指数变化.说明对于低NBTI器件,R-D退化模型中的指数项起主要作用,与文献[13]指出的NBTI退化满足指数模型 eβEox相符.
观察图3中界面反馈对器件寿命曲线的影响可发现,带反馈和不带反馈的寿命曲线变化只是发生了平移,不对寿命变化的指数规律产生显著影响.因此,这时器件即使产生较严重的界面反馈和退化曲线饱和,也不会严重影响寿命的变化规律.该结论似乎难以理解.
3.3 界面电荷引起NBTI退化饱和的分析
由图2和图3可知,界面电荷反馈对器件退化饱和的影响主要由界面电荷数决定,与栅极电压关系不大.但对于低NBTI器件,要有足够高的栅极电压并产生足够多的界面电荷后 (Nit>1012cm-2,即ΔVt>100 mV),才能观察到退化饱和现象.
由器件物理知识可知,氧化层电场Eox是由氧化层中的电势降Vox引起,它满足
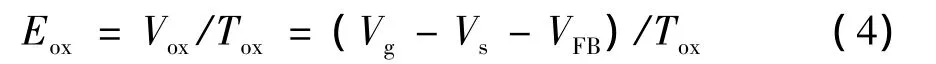
其中,Vs为器件的表面势;VFB为平带电压,在此主要表现为功函数差.NBTI退化产生界面电荷,主要影响表面势,进而影响栅氧化层电场,以及器件退化的饱和程度.NBTI的电荷数对退化饱和的影响存在两种特殊情况:
1)当栅压较大 (Vg取值-3.2~-3.6 V)且变化时,NBTI退化产生的界面电荷数大于1×1012cm-2,会对表面势Vs有一定的影响,但此时器件都处于深度反型状态,Vs的变化量主要受界面电荷数的影响,和此时的栅压关系不大.这种情况对应于器件材料参数ARD较小、低NBTI器件,需较大的栅压才能观察到退化饱和.
2)当栅压较低 (Vg取值-1.0~-2.2 V)且变化时,虽然器件是处于强反型状态 (导通状态),但反型的深度较轻,此时Vs的变化量不仅受界面电荷数的影响,和栅压也密切相关.这种情况对应于器件材料参数ARD较大、高NBTI器件,只需较小的栅压就能产生明显的退化饱和.
对于低NBTI器件,由于材料参数ARD较小,当栅压较低时不能产生足够的界面电荷,也就观察不到这种低栅压退化饱和现象.但如果器件材料参数ARD较大时,情况是否会有不同?
3.4 高NBTI器件界面反馈引起的饱和
高NBTI器件的ARD参数较大.由式(2)和3.1节讨论的R-D模型参数取值,本研究设kr=2.31×10-11cm3/s,kH=1.40 × 10-3cm3,取值都在文献的报道范围内[7,12,14],其他参数不变,这时计算得ARD=5.6×10-2s-1/6.重新数值模拟绘制的器件阈值电压漂移随退化时间的变化如图4.
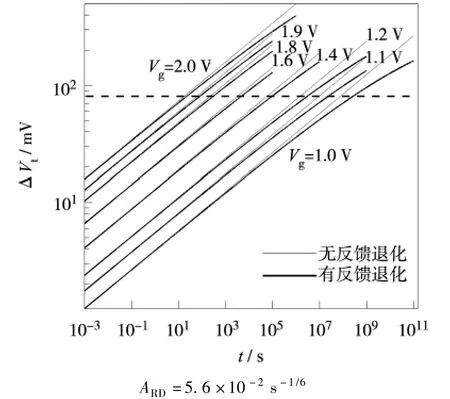
图4 高NBTI器件阈值电压退化饱和现象Fig.4 The saturation phenomenon of ΔVtin the high NBTI device
高NBTI器件的界面反馈由界面电荷和栅极电压两个因素决定.与低NBTI器件不同,首先当界面电荷数大于Nit>1×1011cm-2时,就可能出现明显的退化饱和现象,如图4中的Vg=-1.0 V曲线所示;其次在相对较短的退化时间内就可能出现退化饱和现象,如图4中的Vg=-2.0 V曲线所示;还有更重要的是对于相同阈值电压漂移 (界面电荷),不同栅压时的饱和程度不相同,栅压较小伴随着越大的饱和,和实验数据[14]相符.
3.5 高NBTI器件的寿命
将图4阈值电压退化数据,仍以失效标准FC=80 mV(退化程度为11.4%)时对应取出器件的退化时间作为寿命,作得寿命随栅压的变化如图5.
对于高NBTI器件,不同的栅压伴随着不同程度的退化饱和,高栅压伴随着较小的退化饱和;低栅压伴随着较大的退化饱和,使得退化外延曲线满足幂指数的变化规律[15],其变化斜率为3.9,和实验数据发现的规律[16]一致.
当以5 a(1.6×108s)作为器件的寿命时,器件的工作电压为1 V.无界面反馈的外延曲线在工作电压为1 V时,将器件寿命低估了4.3倍.由此可见,对于高NBTI器件,界面电荷反馈对寿命的估算有重要影响.

图5 高NBTI器件的寿命变化曲线Fig.5 Vgdependence of lifetime in the high NBTI device
结 语
本研究利用二维器件数值模拟方法,得到pMOS器件的栅氧化层电场和沟道空穴浓度,用于计算NBTI效应R-D模型中给出的界面电荷.再利用二维数值模拟软件考虑这个界面电荷对器件栅氧化层电场和沟道空穴浓度的影响,从而能够对器件界面反馈的形态和作用进行分析.通过大量计算,并与已有的实验数据比对研究,得出:
1)界面反馈使器件退化减小,有别于以往对退化饱和的各种解释,是一种新的NBTI退化饱和机制,对不同类型器件寿命有不同的影响.本研究主要分析高/低NBTI两种器件因NBTI界面反馈引起的寿命曲线变化.
2)在低NBTI器件中,界面反馈主要由界面电荷量决定,界面电荷数在1×1012cm-2以上,存在明显的反馈作用,才可能在实验中观察到.反馈形态类似硬饱和现象,对器件寿命曲线的变化影响不大.器件寿命曲线趋于满足指数变化规律.
3)在高NBTI器件中,界面反馈由界面电荷和栅极电压决定,当栅压较低时,界面电荷数大于1×1011cm-2就能观察到明显的反馈作用.对于同样的退化程度 (寿命),栅压越低伴随着越大的退化时间延长 (饱和),和实验发现的退化饱和现象以及变化规律相符.正是这种退化饱和使得高NBTI器件的寿命曲线变化基本满足幂指数变化规律.
/References:
[1] Bénard C,Math G,Fornara P,et al.Influence of various process steps on the reliability of PMOSFETs submitted to negative bias temperature instabilities[J].Microelectronics Reliability,2009,49(9/10/11):1008-1012.
[2]Mahapatra S,Islam A E,Deora S,et al.A critical reevaluation of the usefulness of R-D framework in predicting NBTI stress and recovery[C]//IEEE International on Reliability Physics Symposium.Monterey(USA):IEEE Press,2011:6A.3.1-6A.3.10.
[3]Alam M A,Kufluoglu H,Varghese D,et al.A comprehensive model for PMOS NBTI degradation:recent progress[J].Microelectronics Reliability,2007,47(6):853-862.
[4]Alam M A,Kufluoglu H.On quasi-saturation of negative bias temperature degradation[C]//The 208th Meeting of the Electrochemical Society(ECS).Los Angeles(USA):[s.n.],2005:139-145.
[5]Grasser T,Gös W,Kaczer B.Dispersive transport and negative bias temperature instability:boundary conditions,initial conditions,and transport models [J].IEEE Transactions on Device Material Reliability,2008,8(1):79-97.
[6]Entner R,Grasser T,Triebl O,et al.Negative bias temperature instability modeling for high-voltage oxides at different stress temperatures[J].Microelectronics Reliability,2007,47(4/5):697-699.
[7]Islam A E,Kufluoglu H,Varghese D,et al.Recent issues in negative bias temperature instability:initial degradation,field dependence of interface trap generation,hole trapping effects,and relaxation [J].IEEE Transactions on Electron Devices,2007,54(9):2143-2154.
[8]Cao Jianmin,He Wei,Huang Siwen,et al.Dependence of the DC stress negative bias temperature instability effect on the basic device parameters in pMOSFET [J].Acta Physica Sinica,2012,61(21):217305-1-217305-8.(in Chinese)
曹建民,贺 威,黄思文,等.pMOS器件直流应力负栅压偏置温度不稳定性效应随器件基本参数变化的分析 [J].物理学报,2012,61(21):217305-1-217305-8.
[9]Cogenda Pte Ltd.Genius User's Guide V.1.7.4 [M/OL].Singapore:Cogenda Pte Ltd,2009.[2009-10-01].http://www.cogenda.com.
[10]Chuang C T.Modeling,analysis,and TCAD of nanoscale devices and circuits[C]//IEEE International Symposium on Circuits and Systems.Taipei:IEEE Press,2009:2305-2308.
[11]Reisinger T,Blank O,Heinrigs W,et al.Analysis of NBTI degradation-and recovery-behaviour based on ultra fast VT measurements[C]//Proceedingson 42nd Annual IEEE International on Reliability Physics Symposium.San Jose(USA):IEEE Press,2006:448-453.
[12]Kumar S V,Kim C H,Sapatnekar S S.A finite-oxide thickness-based analytical model for negative bias temperature instability[J].IEEE Transactions on Device and Material Reliability,2009,9(4):537-556.
[13]Krishnan A T,Chakravarthi S,Nicollian P,et al.Negative bias temperature instability mechanism:the role of molecularhydrogen [J]. Applied Physics Letters,2006,88(15):153518-1-153518-3.
[14]Aono H,Murakami E,Okuyama K,et al.Modeling of NBTI degradation and its impacton electric field dependence of the lifetime[J].Microelectronics Reliability,2005,45:1109-1114.
[15]Cao Yanrong,Ma Xiaohua,Hao Yue,et al.Models and related mechanisms of NBTI degradation of 90 nm pMOSFETs[J].Chinese Journal of Semiconductors,2007,28(5):665-669.
[16]Ji Z G,Lin L,Zhang J F,et al.NBTI lifetime prediction and kinetics at operation bias based on ultrafast pulse measurement[J].IEEE Transactions on Electron Devices,2010,57(1):228-237.
2012-10-24;
2013-02-09
Numerical analysis of device lifetime change caused by interface feedback under NBTI stress
Cao Jianmin†,He Wei,Huang Siwen,and Zhang Xulin
College of Electronic Science and Technology,Shenzhen University,Shenzhen 518060,P.R.China
A joint calculation method of 2D device simulation and negative bias temperature instability(NBTI)equations was proposed in this paper,which could be used to analyze the feedback of the created interface charge by NBTI effects on pMOS device gate oxide electric field and channel hole concentration.The analysis results show that when the interface charge of NBTI is generated to a certain extent,the degradation is decreased due to the interface feedback.The feedback of this interface charge to make NBTI degradation decreases is a new kind of saturation mechanism of degradation,which has a different influence on different types of devices.In the low NBTI devices,the interface feedback has little effect on the device lifetime curve.The device lifetime curve tends to meet the exponential variation;while in the high NBTI devices,the interface feedback makes the life curve of the device to meet basically the power law variation.
semiconductor technology;metal oxide semiconductor field effect transistor;negative bias temperature instability;computer aided design;interface feedback;lifetime
TN 386.1;TN 306
A
10.3724/SP.J.1249.2013.02144
Foundation:National Natural Science Foundation of China(11109052);Shenzhen Science and Technology Development Funds(201005280558A)
†
Senior engineer Cao Jianmin.E-mail:jmcao@szu.edu.cn
:Cao Jianmin,He Wei,Huang Siwen,et al.Numerical analysis of device lifetime change caused by interface feedback under NBTI stress [J].Journal of Shenzhen University Science and Engineering,2013,30(2):144-149.(in Chinese)
国家自然科学基金资助项目 (11109052);深圳市科技发展计划资助项目 (201005280558A)
曹建民 (1964-),男 (汉族),陕西省榆林市人,深圳大学高级工程师、博士.E-mail:jmcao@szu.edu.cn
引 文:曹建民,贺 威,黄思文,等.NBTI界面电荷反馈引起器件寿命变化的数值分析[J].深圳大学学报理工版,2013,30(2):144-149.
【中文责编:英 子;英文责编:雨 辰】
