FWD动载下的横观各向同性路基动力响应分析
2013-05-12栗振锋
栗振锋,张 敏
太原科技大学交通与物流学院,太原 030024
FWD动载下的横观各向同性路基动力响应分析
栗振锋,张 敏
太原科技大学交通与物流学院,太原 030024
利用有限元分析原理,建立基于横观各向同性路基的三维仿真模型,分析在落锤式弯沉仪(falling weight deflectometer,FWD)脉冲动载作用下路基表面的弯沉,及不同深度处力学指标的变化,讨论土基材料横观各向同性对力学指标的动力响应影响.结果表明,路基弯沉峰值随距荷载中心点距离的增大而滞后,荷载中心点与距荷载中心200 mm处传感器点的滞后幅度最大 (为60%);弯沉值随水平模量的增大而减小,最大减小幅度为21%;路基所受应力随深度的增加而减小,最大减小幅度为67%;水平模量的增大也会减小应力值,最大减小幅度为28%.落锤式弯沉仪能较好模拟车辆移动荷载状况,反映实际路面受力情况,基于横观各向同性的土质路基,能有效地预测路基的使用性能.
道路工程;横观各向同性;路基;三维有限元;落锤式弯沉仪;动力响应
迄今,路面设计方法国内外通常采用静载荷作用下的地基模型,但实际的路面载荷是随时间变化的动态值,采用静态荷载会给路面分析带来较大误差.为更深入研究动载下路面的破损机理,并改进路面设计的力学模型,有必要研究动载下路面的响应分析.把道路材料结构假定成均质、弹性、各向同性的材料是不符合实际的,尤其是松散的粒状类基层和土质路基,具有非线性特性,用横观各向同性的弹性模型来预测土基的动力响应效果更好[1-5].弯沉是反映路面结构性能的重要指标,随着落锤式弯沉仪 (falling weight deflectometer,FWD)检测技术的快速推广,基于FWD的路面弯沉动力响应研究越来越被重视.本研究借助有限元软件,建立FWD荷载作用下横观各向同性路基的瞬态动力分析模型,对路基在动载作用下的弯沉盆及其应力响应进行数值分析.
1 FWD工作原理
落锤式弯沉仪是目前国际上最先进的路面强度无损检测设备之一,它通过计算机系统控制下的液压系统启动落锤装置,将一定质量的落锤提升到与所加载荷相关的高度,并将其自由落下,形成脉冲荷载,作用于弹簧或橡胶垫[6],并传递到路面,使路面表面产生瞬时变形,很好地模拟了行车载荷对路面的作用,反映了路面结构层在动态荷载作用下的工作性能[7-9].通过距载荷中心点不同距离的5~9个高精度传感器,检测结构层变形,传感器与载荷中心的距离分别为 0、200、305、450、610、914、1 219、1 524和1 829 mm,记录信号并将数据传输至计算机,从而可精准实测荷载作用下的动态弯沉及弯沉盆[7].
2 动力学基本理论
应用弹性动力学的Hamilton变分原理,道路结构在车辆荷载作用下的动态响应有限元基本方程[10-11]为

其中,M、C和K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵;u、˙u和ü分别为位移、速度和加速度向量;F(t)为动载荷向量.
有限元计算中的质量矩阵有2种形式,本研究计算路基结构体的动力响应时,采用一般质量矩阵,阻尼矩阵根据Rayleigh在1877年提出的瑞利阻尼假设来确定,

其中,α和β是与结构固有频率及阻尼比相关的阻尼常系数,可由任意2个振型的固有频率和相应的阻尼比来确定,即
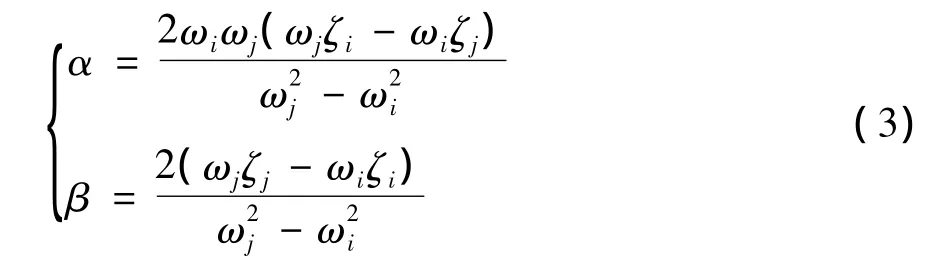
其中,ωi和ωj为任意2个振型的固有频率;ζi和ζj为相应频率对应的阻尼比.
对有限元动力方程 (1)的求解,主要有振型叠加法和直接积分法.本研究采用直接积分法中的Newmark法,作出假设为[12]

其中,γ和β是按直接积分精度和稳定性要求而确定的参数.
Newmark法对线性问题无条件稳定,而且无数值阻尼的影响.对非线性问题,通过自适应步长的选择以及适当增加结构阻尼或数值阻尼,可有效克服非线性问题分析中可能出现的数值失稳.
3 横观各向同性弹性模型
正交各向异性的独立模型参数为3个正交方向的杨氏模量 E1、E2和E3,3个泊松比μ12、μ13和μ23,3个剪切模量G12、G13和G23.若材料某平面性质相同,即为横观各向同性弹性体.假定1~2平面为各向同性平面,那么E1=E2=Ep,μ31=μ32=μtp,μ13= μ23= μpt,G13=G23=Gt,其中 p 和 t分别代表横观各向同性体的横向和纵向.因此,横观各向同性体的应力-应变表达式为[10]

4 模型建立与参数确定
路基模型尺寸(x,y,z)大小为6 m×3 m×3 m,x轴为路基纵向,y轴为路基横向.结构纵向两断面对x方向约束,结构横向两断面对y方向约束,底面全部被约束.模型采用8节点四边形二次减缩积分单元进行网格划分.
FWD荷载圆作用于路基上,半径为0.15 m,作用时间为0.03 s,脉冲荷载随时间的变化为半正弦函数 P=0.7 sin(πt/0.03)MPa[13-14].

图1 FWD脉冲荷载波形图Fig.1 FWD load waveform
土基的各向异性特性已被试验所证实,明海燕等[15-16]分析了砂土各向异性对挡土墙抗震性能的影响,对砂土内各向异性的本构模拟进行了研究.文献[17-20]对粒状类材料的天然各向异性也进行了深入探讨.本文取土基垂直向弹性模量为30 MPa,各向异性度系数a(定义各向异性度系数为横观各向同性体中水平向弹性模量与垂直向弹性模量的比值)分别为0.9、1、2、3 和4[1],即水平向弹性模量分别取27、30、60、90和120 MPa,用以评价水平向弹性模量和垂直向弹性模量之间的异性程度对土基的响应影响,泊松比两个方向统一取0.35,垂直向剪切模量是垂直向弹性模量的1/[2(1+v)]倍[1].
5 有限元结果分析及讨论
图2是各向同性土基在FWD动载作用下,距载荷中心点不同距离各传感器点的弯沉时程曲线图.图3描绘了土基在FWD动载作用下,各向异性度对弯沉的影响.图4给出了各向同性土基在FWD动载作用下,距荷载中心不同深度处垂直应力的时程图.图5为土基在FWD动载作用下,各向异性度对距荷载中心不同深度处应力的影响.

图2 各向同性土基各传感器点的动载弯沉Fig.2 Dynamic load deflection of isotropic soil base at each sensor point
结果表明:①图2显示,各传感器点最大弯沉较荷载峰值有一定滞后,距荷载中心越远,滞后时间越长,这与用FWD实测时传感器不同测点处所测弯沉的时程规律一致,荷载中心点与距荷载中心200 mm处传感器点的滞后幅度最大,为60%.②从图3可见,土基表面弯沉随材料水平模量的增加而降低,降低趋势越来越缓慢,最大下降幅度可达20.8%.③随着距荷载中心处距离的增加,弯沉值越来越小,形成了弯沉盆,不同异性度下土基的弯沉值与各向同性时的值渐趋一致.④从图4可以看出,路基所受压应力随距荷载中心深度的增加而减小,最大减幅为66.6%,到0.8 m处应力值渐趋于0,应力主要由路基表面承担,说明路基表面的功能主要是降低垂直压力,保证路基不出现变形,有足够承载力.⑤从图5可见,随着材料水平模量的增大,路基同一深度处的压应力值变小,最大减幅为 27.7%.

图3 土基横观各向同性对动载弯沉的影响Fig.3 The impact of transversely isotropic to dynamic load deflection
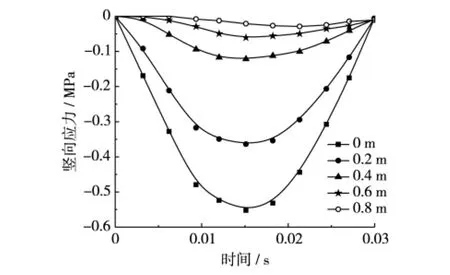
图4 各向同性土基荷载中心不同深度处垂直应力时程图Fig.4 Time chart of vertical stress at load centers different depths

图5 土基横观各向同性对荷载中心不同深度应力的影响Fig.5 The impact of transversely isotropic to vertical stress at load centers different depths
结 语
本研究通过建立横观各向同性路基在FWD脉冲荷载作用下的三维有限元模型,利用有限元动力学原理,对动载 (FWD荷载)作用下土基表面的弯沉与不同深度处的应力,以及路基材料各向异性的影响进行分析评价,与实测数据相比,结果较为准确.用FWD模拟路面移动荷载较为恰当,能真实反映路面的实际受力特性,采用横观各向同性理论进行路基设计能很好地预测路基结构内部受力状况,预测路基的使用性能,更接近路基的实际响应状况,可为路基路面工程结构的施工和研究提供依据.
/References:
[1]Li Zhenfeng,Erol Tutumluer.Asphalt Pavement Design Theory and Method Based on Transversely Isotropic[M].Beijing:China Water Resources and Hydropower Press,2007.(in Chinese)
栗振锋,Erol Tutumluer.基于横观各向同性的沥青路面设计理论及方法 [M].北京:中国水利水电出版社,2007.
[2]Li Zhenfeng,Hu Changshun.Axisymmetric layered elastic half-space problem solving system based on transversely isotropic[J].Journal of Xi'an Highway Traffic University,2001,20(4):8-10.(in Chinese)
栗振锋,胡长顺.横观各向同性轴对称层状弹性体系半空间问题的求解 [J].西安公路交通大学学报,2001,20(4):8-10.
[3]Li Zhenfeng,Hu Changshun.The solution of axisymmetric transversely isotropic semi-infinite surface displacement[J].Journal of Chang'an University,2002,22(5):13-16.(in Chinese)
栗振锋,胡长顺.轴对称横观各向同性半无限体表面位移的求解[J].长安大学学报,2002,22(5):13-16.
[4] Li Zhenfeng,Guo Xiangyun,Wang Binggang,et al.Structural analysis of gravel subbase asphalt Pavement base on axisymmetric transversely isotropic[J].Journal of Taiyuan Science and Technology University,2007(8),28(4):296-299.(in Chinese)
栗振锋,郭向云,王秉刚,等.基于横观各向同性碎石底基层沥青路面结构分析 [J].太原科技大学学报,2007,28(4):296-299.
[5]Li Zhenfeng,Guo Zhongyin.The response model of flexible pavement based on anisotropy[C]//International Innovation Forum for Doctoral Students in Transportation Engineering.Shanghai:International Transportation Commitee,2005.
[6]Cui Hongtao.FWD application in road engineering[J].Highway Transportation Technologies,2002,9(3):23-25.(in Chinese)
崔宏涛.FWD在道路工程中的应用 [J].公路交通技术,2002,9(3):23-25.
[7] Huang Lei,Feng Quan,Yang Yang,et al.Property analysis for pavement based on the role of FWD load [J].Highway Transportation Technologies,2010,4(2):14-20.(in Chinese)
黄 磊,冯 铨,杨 阳,等.基于FWD荷载作用的路面力学指标分析 [J].公路交通技术,2010,4(2):14-22.
[8]Wu Liren.Asphalt pavement dynamic deflection using FWD test[J].Friends of Science,2007(3):49-50.(in Chinese)吴礼任.利用FWD测试沥青路面动态弯沉 [J].科学之友,2007(3):49-50.
[9]Xie Hui,Guo Zhongyin,Cong Lin.Dynamic response of multi-layer elastic system asphalt pavement based on the role of FWD load [J].Transport and Computer,2006,130(3):49-51.(in Chinese)
谢辉,郭忠印,丛林.FWD载荷下的多层弹性体系沥青路面动力响应 [J].交通和计算机,2006,130(3):49-51.
[10]Liao Gongyun,Huang Xiaoming.ABAQUS Finite Element Software Application in Road Engineering[M].Nanjing:Southeast University Press,2008.(in Chinese)
廖公云,黄晓明.ABAQUS有限元软件在道路工程中的应用 [M].南京:东南大学出版社,2008.
[11]Wang Jingchang,Chen Yekai.Application of ABAQUS in Civil Engineering[M].Hangzhou:Zhejiang University Press,2006.(in Chinese)
王金昌,陈页开.ABAQUS在土木工程中的应用[M].杭州:浙江大学出版社,2006.
[12]Liang Qingxiang.Realization of the Finite Element and the MARC [M].Beijing:Machinery Industry Press,2005.(in Chinese)
梁清香.有限元与MARC实现 [M].北京:机械工业出版社,2005.
[13]Hao Dali,Wang Binggang.Dynamic response of pavement structure [J].Journal of Chang'an University,2002,22(3):9-12.(in Chinese)
郝大力,王秉纲.路面结构动力响应分析[J].长安大学学报,2002,22(3):9-12.
[14]Yuan Song,Shan Jingsong.Dynamic response numerical analysis of flexible pavement[J].Journal of Changsha Communications University,2006,22(2):33-37.(in Chinese)
元 松,单景松.基于FWD的柔性路面结构动力响应数值分析 [J].长沙交通学院学报,2006,22(2):33-37.
[15] Ming Haiyan,Li Xiangsong,Dafalias Y F.Numerical study of impact of soil anisotropy on seismic performance of retaining structure[J].Journal of Shenzhen University Science and Engineering,2007,24(3):221-227.(in Chinese)
明海燕,李相崧,Dafalias Y F.砂土各向异性对挡土墙抗震性能影响数值分析 [J].深圳大学学报理工版,2007,24(3):221-227.
[16]Ming Haiyan,Li Xiangsong,Dafalias Y F.Constitutive modeling of fabric aniso-tropy of sand[J].Journal of Shenzhen University Science and Engineering,2007,24(4):331-338.(in Chinese)
明海燕,李相崧,Dafalias Y F.砂土内在各向异性的本构模拟 [J].深圳大学学报理工版,2007,24(4):331-338.
[17]Ching S,Yin Zhenyu.Micromechanical modeling for inherent anisotropy in granular materials[J].Journal of Engineering Mechanics,2010,136(7):830-839.
[18]Ehsan S H.Discrete element modeling of inherently anisotropic granular assemblies with polygonal particles[J].Particuology,2012(10):542-552.
[19] Fu Pengcheng,Yannis F.Study of anisotropic shear strength of granular materials using DEM simulation [J].International Journal for Numerical and Analytical Methods in Geomechanics,2011,35(10):1098-1126.
[20]Mahmud S,Kiichi S.Micromechanical behavior of granular materials with inherent anisotropy under cyclic loading using 2D DEM [J].Granular Matter,2010,12(6):597-605.
2011-05-20;Revised:2012-10-06;
2012-12-06
The analysis of dynamic response of transversely isotropic subgrade based on FWD
Li Zhenfeng†and Zhang Min
Department of Traffic Engineering,Taiyuan University of Science and Technology,Taiyuan 030024,P.R.China
The finite element analysis method was adopted and a three-dimensional simulation model was established for simulating dynamic response of transversely isortopic subgrade.Some mechanical response such as deflection and stress under the effects of Falling Weight Deflectometer were analyzed,and the impact that transversely isotropic subgrade material on the dynamic response was discussed.The results show that subgrade deflection peak is delayed with the increase of the distance from the center of the load,the largest delayed range is between the load center and the sensor point of 200 mm away from the load center,deflection is decreased with the increase of horizontal modulus,the maximum reduction rate is 21%,subgrade stress is decreased with the increase of depth,the maximum reduction rate is 67%,increase of horizontal modulus will decrease the stress value,the maximum reduction rate is 28%.Falling Weight Deflectometer can simulate the vehicle moving load conditions,better reflecting the actual situation of the force to the road;and transverse isotropic can better forecast the performance of the subgrade.
road engineering;transversely isotropic;subgrade;three-dimensional finite element;falling weight deflectometer;dynamic response
U 416.01
A
10.3724/SP.J.1249.2013.02195
Foundation:National Natural Science Foundation of China(51078250);Scientific and Technological Project of Shanxi Province(20120321023-05)
†
Professor Li Zhenfeng.E-mail:lizhenfeng_68@sina.com
:Li Zhenfeng,Zhang Min.The analysis of dynamic response of transversely isotropic subgrade based on FWD [J].Journal of Shenzhen University Science and Engineering,2013,30(2):195-199.(in Chinese)
国家自然科学基金资助项目 (51078250);山西省科技攻关资助项目 (20120321023-05)
栗振锋 (1968-),男 (汉族),太原科技大学教授.E-mail:lizhenfeng_68@sina.com
引 文:栗振锋,张 敏.FWD动载下的横观各向同性路基动力响应分析 [J].深圳大学学报理工版,2013,30(2):195-199.
【中文责编:坪 梓;英文责编:之 聿】
