一步成形模拟中一种新的松弛因子搜索算法

张亚奇，王 舒，刘伟杰，张向奎，胡 平，郑国君

（1. 大连理工大学 运载工程与力学学部 汽车工程学院，大连 116024；2. 大连理工大学 工业装备结构分析国家重点实验室，大连 116024；3. 大连迪克斯科技有限公司，大连 116024）

一步成形模拟中一种新的松弛因子搜索算法

张亚奇1,2，王 舒2，刘伟杰1,2，张向奎1,2，胡 平1,3，郑国君3

（1. 大连理工大学 运载工程与力学学部 汽车工程学院，大连 116024；2. 大连理工大学 工业装备结构分析国家重点实验室，大连 116024；3. 大连迪克斯科技有限公司，大连 116024）

0 引言

车身覆盖件冲压成形是汽车生产中一个很重要的环节，制约着汽车质量的提高和改型换代周期的缩短，传统的依靠经验进行反复调试的模具设计方法已经不能满足高质量、高效率和低成本的要求。随着CAD和CAE技术的发展，板料冲压成形模拟技术越来越多的被用于预测变形路径和成形缺陷如裂纹和起皱。

板料成形模拟技术是基于大变形弹塑性有限元理论的一种数值模拟算法，主要可分为增量理论和全量理论[1]。增量理论的思想是将整个变形分为若干个小增量步，第i步的求解是建立在第i-1步所得的结果之上的，迭代到最后可以得到最终的模拟结果，增量法最主要的优点是模拟精度高，但其计算复杂，数据准备繁琐，计算时间长，不能满足在模具最初设计阶段快速估计产品可制造性的要求。

一步成形模拟方法是一种基于全量理论的有限元逆算法[1]，该方法最早由Kobayashi等人[2]提出，J. L. Batoz，Y. Q. Guo 和H. Hub都进行过研究[3～5]。这种方法假设变形过程是比例加载的，只考虑初始毛胚板和变形终了构型两个状态，忽略中间状态，建立有限元方程。其突出优点是计算效率高并且拥有较好的精确性。既可以在产品的初始设计阶段快速预测冲压件的成形性，还可以在制造阶段快速估计毛胚板料的尺寸和形状，应用前景广泛。

一步成形模拟最终需要求解一个大规模非线性方程组，一般采用Newton-Raphson（N-R）算法进行迭代求解[5]，但是经典的Newton-Raphson迭代对初始解的精度要求比较苛刻，初始解必须在真实解附近，迭代才能收敛。对于一些复杂问题尤其是高度非线性的问题，很难找到让经典的N-R迭代收敛的初始解。因此为了放松对初始解的要求，提高迭代稳定性和收敛速度，通常需要引入松弛因子。松弛因子的取值对求解的稳定性和计算效率有很大的影响。如果松弛因子取值太大，则容易发生“指数溢出[6]（Exponential Overflow）”，即计算将以无结果中止；如果松弛因子太小，会使计算效率变差，增加程序的运行时间。

在一步成形模拟求解过程中，选取合适的松弛因子比较困难，而且到目前为止国内外对这方面的研究还比较少，国外还没有文章对其进行专门的研究，即便是涉及到松弛因子的文章，大部分也没有给出算法的具体步骤。Sven K. Esche等[7]比较了多种松弛因子线性搜索方法；L. Armijo[8]首先采用“折半搜索”的方式确定松弛因子，该方法也被称为Armijo Rule，在一步成形模拟中有广泛应用。国内吉林大学的那景新和陆善斌等人[9]提出了松弛因子的黄金分割算法，用一维搜索0.618法确定松弛因子的取值；那景新，高华等人[1]采用插值抛物线近似替代目标函数，优化松弛因子的取值。上述两种算法的迭代收敛性和计算效率都比固定松弛因子的算法要好，但都比较复杂，需要的附加计算较多。现有的处理方案一般采用“折半搜索”算法，但由于其算法粗糙，不适合处理一些复杂问题。本文在权衡迭代稳定性和计算效率的基础上提出了一种新的松弛因子搜索算法，并验证了其有效性。

1 一步成形基本理论

一步成形有限元方法的基本思想是假设变形过程是比例加载的，通过比较初始毛胚板和变形终了构型两个状态，确定零件中的节点在毛胚平板中的对应位置，从而得到毛胚平板的形状和尺寸，进而得到零件中的应变、应力分布和厚度分配。在零件变形终了构型上建立虚功方程[5]：

选取松弛因子的方法有很多[6]，通常的办法是定义一个目标函数φ，选取合适的松弛因子使该函数的值随着迭代的进行逐渐减小，下面是常用的一种目标函数形式：

对于某些问题，松弛因子经过一到两次减半就可以使目标函数减小，“折半搜索”在解决这类问题时效果较好，但是作为一种初级的线性搜索算法，“折半搜索”由于搜索模式单一，只有减半这一种方式，造成其在处理一些问题时太粗糙。因为松弛因子只能取1、0.5、0.25、0.125、0.0625、0.05这六个值中的某一个，这很有可能错过一些较大的松弛因子（如0.8，0.9），例如在某个迭代步中，最佳的松弛因子取值为0.75，显然“折半搜索”会错过0.75，而得到一个较小的松弛因子，影响计算效率。

2 新的松弛因子搜索算法

不难看出，最理想的情况是可以找到使目标函数在区间上取最小值的松弛因子[10]，但一般情况下目标函数非常复杂，搜索最小值点的过程需要大量试算，这会增加搜索松弛因子的时间消耗，降低程序的计算效率。本文在权衡迭代收敛性和计算效率的基础上，提出了一种基于局部极小值搜索的新松弛因子搜索算法，算法的思想是用局部极小值点代替最小值点，并通过一个简单的线性搜索得到目标函数的局部极小值点。算法的具体操作步骤如下：

1）首先令松弛因子为1，计算目标函数的值，如果相比上一个迭代步有所下降，则取松弛因子为1，否则开启目标函数的局部极小值搜索算法。

2）目标函数的局部极小值搜索算法：

（1）沿0向1的方向进行搜索，确定a和c的值，满足条件；

（2）继续搜索，确定b的值，满足条件，同时保持的关系不变。

算法的思想是，用一个长度为0.1的区间沿着0向1的方向移动，每次移动步长，直到找到满足条件的区间或者达到预先设置的最大值1。

算法的流程如图1所示。

图1 新松弛因子搜索算法流程图

3 数值算例

为了验证本文提出的新算法的有效性，作者编制计算机程序实现了新算法，并将其加入到KMAS/One-Step程序中。本文选取了U型梁、方盒等四个算例进行测试分析，并与“折半搜索”算法结果进行比较。测试所用硬件配置为Intel Core i5/2.53GHz，8GB内存。

各测试零件均采用三角形单元划分有限元网格，具体划分情况如表1所示。出于篇幅考虑，这里只给出了方盒和测试零件四的有限元模型图如图2所示。

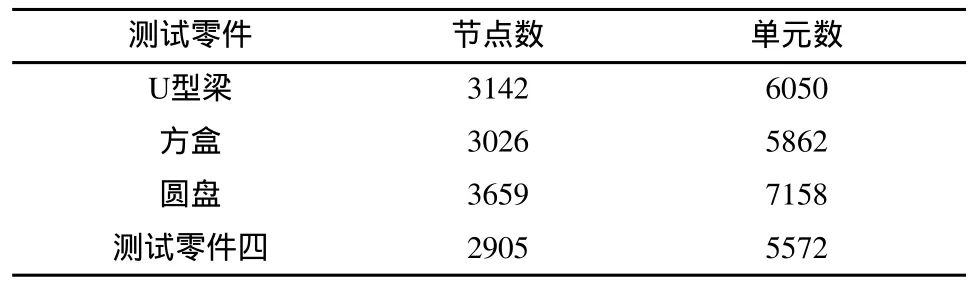
表1 测试零件的有限元网格划分情况

图2 方盒（左）和测试零件四（右）的有限元模型

测试零件所用材料为钢，具体的材料和几何参数如表2所示。

表2 测试零件的材料和几何参数

由于篇幅限制，这里只列出部分计算结果图。在四个算例中，方盒最具有代表性，下面给出了采用本文提出的新松弛因子搜索算法计算所得的方盒的厚度分布图和初始毛胚平板形状如图3所示。

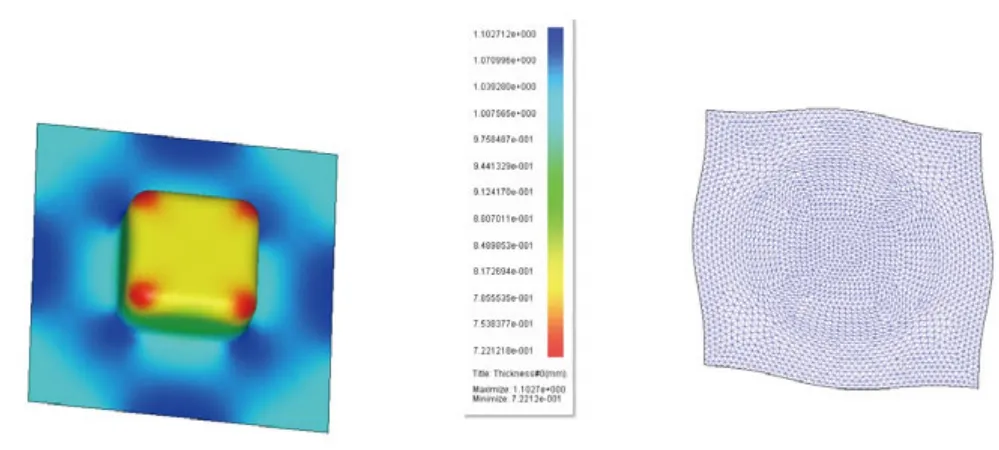
图3 方盒的厚度分布图（左）和毛胚形状（右）

表3为采用不同算法对四个算例进行测试的结果，包括零件的最大和最小厚度（mm），迭代收敛所需的步数和迭代消耗的CPU时间（s）。

根据表3，我们可以看出，对于选取的四个算例，采用两种松弛因子选取算法迭代都可以收敛，而且计算所得的零件最大（最小）厚度相差无几，这表明本文提出的新松弛因子搜索算法不影响Newton-Raphson迭代的收敛性和计算精度。

新松弛因子搜索算法可以有效减少收敛所需的迭代步数，尤其是在处理一些深拉延问题时。例如圆盘的迭代步数从11减少到5。这主要是因为新算法搜索目标函数的局部极小值点，而“折半搜索”只要求目标函数下降。但是新算法要比“折半搜索”复杂，搜索松弛因子的时间也长，因此在解决某些问题时，时间略有上升，这是正常的。为了减少不必要的附加计算，本算法并不是每次都开启局部极小值搜索，而是分情况处理，在松弛因子取1目标函数无法下降时，才进行搜索。

表3 不同松弛因子算法的测试结果

对于规模较大的问题，解方程组的时间可以占到一步成形模拟程序总时间的90%以上[9]。本文提出的新算法可以有效减小收敛所需的迭代步数，虽然目标函数的局部极小值搜索会带来一些附加计算，但是解线性方程组的时间复杂度为o(n3)，新松弛因子搜索算法的时间复杂度为o(n2)，因此可以预见新算法在解决大型问题时，计算效率的提高将更加明显。新算法可以使目标函数随着迭代的进行逐渐减小，因此可以放松对初始解的要求，提高N-R迭代的稳定性。

总体来说，本文提出的新的松弛因子搜索算法，比传统的“折半搜索”算法有更好的迭代稳定性和计算效率，尤其是在处理规模较大的问题时。

4 结论

本文研究了一步成形模拟中非线性方程组的N-R迭代求解，探讨了松弛因子取值对N-R迭代收敛性和计算效率的影响，并在权衡迭代稳定性和计算效率的基础上，提出了一种新的基于局部极小值搜索的松弛因子搜索算法。选取了U型梁和方盒等四个实例，验证了新算法的有效性。通过与经典的“折半搜索”算法的结果进行比较，本文发现新算法可以有效减少迭代收敛所需的步数，提高计算效率，在处理大型问题时，优势将更加明显。本文提出的新松弛因子搜索算法已经集成到Siemens PLM NX/One-Step和KMAS/One-Step中。

[1]那景新,高华,张丽,胡平.一步成形模拟方法中松弛因子选取算法[J].吉林大学学报(工学版),2005,3:292-296.

[2]Kobayashi S, Kim J H, Mechanics of Sheet Metal Forming,New York: Plenum Press,1978:341-365.

[3]Yang Shiyong and Nezu Kikuo,“Application of an inverse FE approach in the concurrent design of sheet stamping”,Journal of Material Processing Technology,1998:79,86-93.

[4]C. H. Lee and H. Huh,“Blank design and strain estimates for sheet metal forming processes by a finite element inverse approach with initial guess of linear deformation”, Journal of Materials Processing Technology,1998:82,145-155.

[5]Y. Q. Guo and J. L. Batoz,“Finite element procedures for strain estimations of sheet metal forming parts”,International Journal for Numerical Methods in Engineering,1990:30,1385-1401.

[6]C. T. Kelley, Solving Nonlinear Equations with Newton’s Method, Philadelphia:Society for Industrial and Applied Mathematics, 2003:1-24.

[7]Sven K. Esche, Gary L. Kinzel and Taylan Altan,“Issues convergence improvement for non-linear finite element programs”,Int. J.Numer.Meth.Engng.1967:40,4577-4594 .[8]L.Armijo,“Minimization of functions having Lipschitz-continuous first partial derivatives”,Pacific J.Math.1966:16,1-3.

[9]陆善彬.一步模拟中冲压方向、单元模型及松弛因子算法研究[D].吉林大学,2004.

[10]Y. Q. Guo,J.L.Batoz, H. Naceur, S. Bouabdallah,F.Mercier, O. Barlet, “Recent developments on the analysis and optimum design of sheet metal forming parts using a simplified inverse approach”,Computers and Structures,2000:78,133-148.

A new relaxation factor search algorithm in one-step forming simulation

ZHANG Ya-qi1,2, WANG Shu2, LIU Wei-jie1,2, ZHANG Xiang-kui1,2, HU Ping1,3, ZHENG Guo-jun3

本文着重研究了一步成形模拟中松弛因子取值对迭代收敛性和计算效率的影响，在权衡迭代稳定性和计算效率的基础上，提出了一种新的松弛因子搜索算法，然后用计算机程序实现了算法，并将其加入到KMAS/One-Step中，通过U型梁、方盒等四个计算实例，与经典的“折半搜索”算法结果进行了比较，验证了新算法的有效性。

板料冲压成形；一步成形；松弛因子

张亚奇（1989 -），男，硕士研究生，主要从事汽车覆盖件冲压成形仿真研究。

TP391

A

1009-0134(2013)06(上)-0014-04

10.3969/j.issn.1009-0134.2013.06(上).05

2013-04-09

863计划项目（2013AA040501）