浅谈非正交分解法在曲线运动问题中的应用

汪 飞

(江苏省海门中学,江苏 南通 226100)

正交分解法是高中物理中研究曲线运动问题的基本方法,但在对一些特殊的曲线运动问题的研究中,若采用正交分解法,问题的研究过程会比较繁琐,甚至需要借助高等数学知识才能使问题得以顺利解决.此时若采用非正交分解法,往往能使问题得到巧妙的解决.为此,下面通过对几道典型的曲线运动问题的分析来展示非正交分解法的巧妙性.

1 斜抛运动

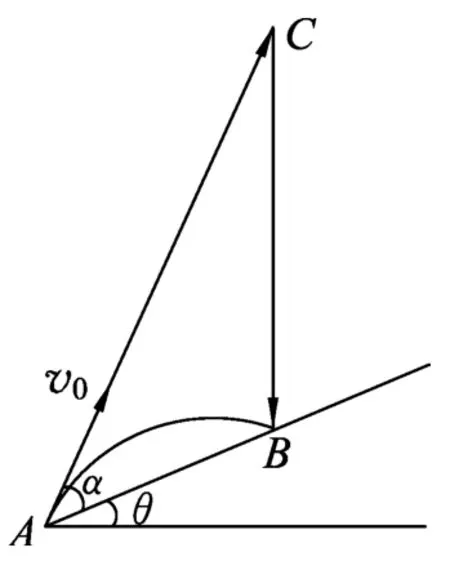
图1

例1.如图1所示,倾角为θ的无限长斜面,在斜面底端A点以与斜面夹角为α的初速度v0抛出一物体,求物体落到斜面上的位置B与斜面底端A点间的距离.

解析:如图1所示,运用非正交分解法将斜抛运动AB分解为沿初速度v0方向的匀速直线运动AC和竖直方向的自由落体运动在矢量三角形ACB中,由正弦定理得

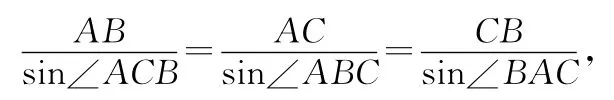
点评:通过对斜抛运动进行非正交分解,避免了正交分解法中通过轨迹的抛物线方程和直线方程的交点求距离的繁琐运算,简洁巧妙地解决了问题.

2 弹道曲线

例2.如图2所示,在某座高为h的山顶A处有一火炮以水平速度v0发射一质量为m的炮弹,经过一段时间后落到山下的地面B处,落地速度与水平方向的夹角为α,炮弹在运动过程中受到的空气阻力的大小与速度成正比,即f＝kv,k为常数,v为炮弹在运动过程中的速度,方向始终与速度方向相反,重力加速度为g.求炮弹落到地面上B点的速度大小.

解析:炮弹在运动过程中受到的空气阻力是与速度有关的变力,做变加速曲线运动,如图3所示,应用非正交分解法,对炮弹在抛出点A点的初速度进行分解分解,则使分速度v1引起的空气阻力与重力平衡,即f1＝kv1＝mg,则炮弹的变加速曲线运动可视为沿竖直向下v1的匀速直线运动和沿v2方向的在变力f2＝kv2作用下的变减速直线运动的合运动.

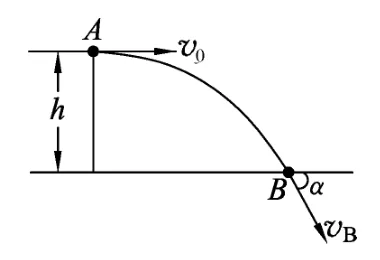
图2

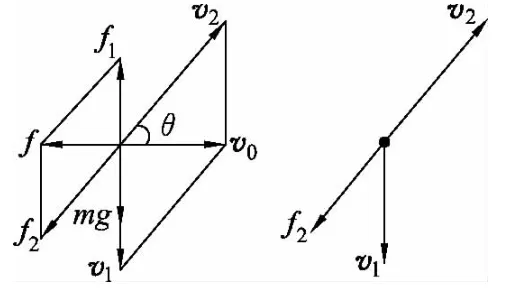
图3

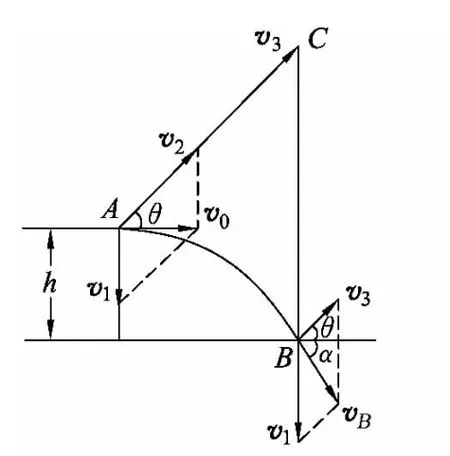
图4

如图4所示,炮弹运动过程中,合位移与分位移的关系为AB＝AC＋CB,沿CB方向做速度为的匀速直线运动,沿AC方向在变力f＝kv2作用下做初速度为v2的变减速直线运动.设v2与v0的夹角为θ,则炮弹到达落地点B时,沿AC方向的速度减为v3,v3与水平方向的夹角为θ,落地速度与水平方向的夹角为α.

对落地点B的速度合成图形中应用正弦定理得

解得

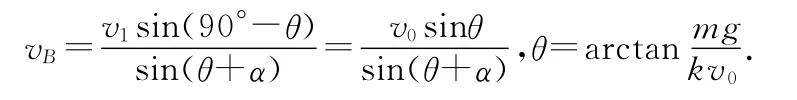
点评:本题中炮弹在受到与速度有关的变力作用下做变加速曲线运动,若采用正交分解法,则水平方向和竖直方向均为变加速直线运动,应用高中的物理和数学知识将无法求解,需借助高等数学知识来求解水平和竖直方向的动力学微分方程.而采用非正交分解法,通过对炮弹的初速进行分解,将变加速曲线运动分解为便于分析的匀速直线运动和变加速曲线运动,应用简单的数学知识便使问题得到巧妙的解决.充分显示了非正交分解法在研究与速度有关的变力作用下做变加速曲线运动问题中的巧妙性.

3 摆线运动

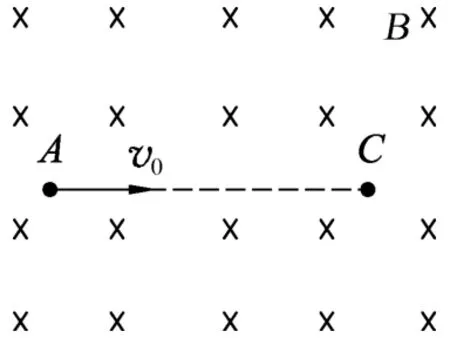
图5

例3.(2013年“北约”自主招生第10题)如图5所示,水平面上方某一足够大的空间存在水平向里的匀强磁场,磁感应强度大小为B,现从磁场中的A点垂直于磁场方向水平发射一个带电粒子,质量为m,电荷量为q,考虑粒子的重力,问:(1)如果粒子从A水平运动到C,AC距离为L,求粒子的速度v0大小？(2)如果速度不满足上问时,粒子速度无论多大都能到达C点,试求AC的距离L应该满足的条件？A到C的时间为多少？(3)如果初速度为0,问是否可能到达C点,在此过程中,最大速度为多少？

解析:(1)粒子沿直线由A运动到C,则要求重力和洛伦兹力平衡,有mg＝qv0B,解得粒子带正电.

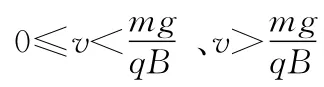
此问中要求无论初速度v多大时,粒子均能到达C点,需要对初速度的方向和大小进行分类讨论,如v＜0、时的粒子运动情形进行分析,能够很好地考查学生对摆线运动情形的掌握程度和思维的严密程度.下面以时的运动情形为例进行分析.

当v＞v0时,如图6所示,将初速度v分解为同一直线上的v0和v′,使洛伦兹力若使f0＝qv0B＝mg,即v0产生的洛伦兹力与重力相平衡,将粒子的变加速曲线运动分解为以速度v0的匀速直线运动和在洛伦兹力f′＝qv′B作用下的匀速圆周运动.

例如,当v′＜v0时,运动轨迹为如图7所示的周期性的摆线图像.当粒子处于轨迹的最低点时,v0与v′同向,当处于轨迹的最高点时,v与v′反向,运动的周期一个周期前进的距离为,与粒子初速度的大小无关.当A、C间距离为d的整数倍时,即当L＝nd＝时,粒子能够到达C点.

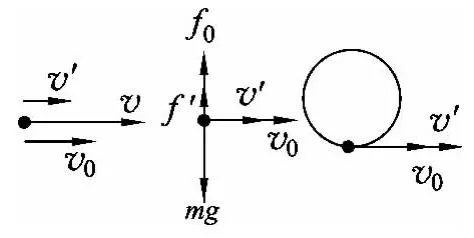
图6

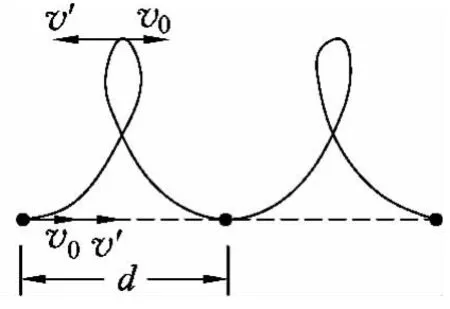
图7

(3)粒子的初速度为0时,为了平衡重力,可将初速度0分解为0＝v0－v0,此时粒子的轨迹如图8所示,一个周期前进的距离d＝故能够到达C点,运动过程中速度的最大值位于轨迹的最低点处

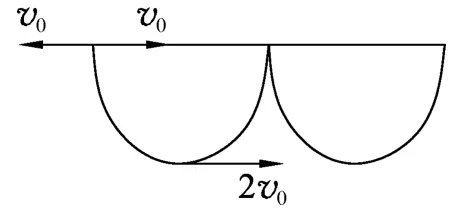
图8

点评:摆线运动是带电粒子在复合场中的一种特殊运动问题,在1996年第13届全国高中物理竞赛决赛第2题、2008年江苏高考第14题和2011年福建高考第22题均对此类问题进行了不同角度的考查,此类问题能力立意高,能充分考查学生的分析综合能力,体现出试题的选拔功能,因此受到各级考试命题专家的青睐.带电粒子在复合场中做变加速曲线运动时,受到与速度相关的变力——洛伦兹力,应用非正交分解法对粒子的初速度进行分解,将粒子的变加速度曲线运动分解为匀速直线运动和匀速圆周运动,巧妙地分析了带电粒子的摆线运动,再次显示了非正交分解法的巧妙性.

4 小结

本文通过应用非正交分解法对几类曲线运动问题进行了分析,此类试题能力要求高,属于高校自主招生和中学物理竞赛范畴,自主招生和物理竞赛试题主要体现试题的选拔功能,因此更加注重解题方法选取的巧妙性.为此,在非正交分解法应用的教学过程中,可选用此类特殊的曲线运动问题进行讲评练,使学生感悟到非正交分解法的巧妙性,丰富学生研究曲线运动问题的分解方法,拓宽学生的视野,加深学生对运动的合成与分解特征的理解.