基于量子逻辑的确定型正则文法＊

王拥兵，张丽霞，雷红轩

（1.安庆师范学院数学与计算科学学院，安徽 安庆246013；2.内江师范学院数学与信息科学学院，四川 内江641112）

1 引言

在经典计算机理论中，自动机和文法都是计算机中简单而又常见的数学模型。它不仅是计算机科学的理论基础，同时在汇编语言、编译语言以及算法设计等方面有重要的应用［1～5］。文献［6，7］将自动机状态集量子化，进一步推广了经典自动机理论，引入了作为量子计算机的简单模型的量子自动机。由于Shor［8］于1994年发现了在量子计算机上进行大数分解的多项式时间算法，以及Gover［9］发现了平方根时间的量子搜索算法之后，量子计算日益受到人们的关注与重视，量子计算模型便是其中一个很重要的研究课题。由应明生等［10～16］建立的基于量子逻辑的自动机和文法理论是量子计算模型方面的一个重要研究方向。特别地，在文献［12］中给出了基于量子逻辑的自动机对应的Kleene定理表现形式，但量子逻辑意义下的Kleene定理成立要依赖于正交模格中子集的交换子的条件。而文献［15］从另一个角度出发，通过引入广义的子集构造方法，证明了基于量子逻辑的有穷自动机与基于量子逻辑的确定型自动机可以相互转化，进而证明了Kleene定理。本文从文法的角度出发，考虑基于量子逻辑意义下的确定型正则文法，证明了基于量子逻辑的确定型正则文法与基于量子逻辑的确定型自动机是可以相互转化的，并给出了量子确定正则语言的代数刻画和层次刻画以及关于正则运算的封闭性。这些结果进一步丰富了自动机和文法理论。

2 ℓ－值确定型正则文法

量子逻辑是指真值为完备正交模格ℓ的逻辑，也称为正交模格值逻辑，见文献［10～15］。本文采用文献［15］的有关记号。完备的正交模格是七元组ℓ＝ 〈l，≤，∧，∨，⊥，0，1〉，其中：

（1）ℓ＝ 〈l，≤，∧，∨，⊥，0，1〉是完备格，1和0分别是最大元和最小元，≤是偏序，对X⊆l，∨X、∧X分别表示X的上确界与下确界。

（2）一元运算⊥是ℓ上的正交补，满足如下条件：∀a，b∈l，

①a∧a⊥＝0，a∨a⊥＝1。

②a⊥⊥＝a。

③a≤b蕴含b⊥≤a⊥。

很容易看出，条件③与De Morgan对偶律是等价的：即 ∀a，b∈l，

③′（a∧b）⊥＝a⊥∨b⊥，（a∨b）⊥＝a⊥∧b⊥。

一个正交模格就是满足如下正交模律的正交格：∀a，b∈l，

④a≤b蕴含a∨（a⊥∧b）＝b。

在正交模格ℓ上定义蕴含算子→满足 ∀a，b∈l，a→b＝1当且仅当a≤b。本文假设→表示Sasaki蕴含，即a→b＝a⊥∨（a∧b）。双蕴含的定义为：∀a，b∈l，a↔b＝（a→b）（b→a）。正交模格值逻辑（即量子逻辑）的语法与经典一阶逻辑类似。 、∨、→是三个原始连接词，∃是原始量词，∧、↔是由 、∨、→和∃定义的。语义方面，将 、∨、→分别理解为ℓ中的⊥、∨、→运算，∃解释为ℓ中的最小上界。集合论公式x∈A的真值为 x∈A ＝A（x）。公式φ是有效的当且仅当 φ ＝1，并记为｜＝ℓφ。

定义1［15］ℓ－值有穷自动机（简记为ℓ-VFA）是五元组 M ＝ （Q，Σ，δ，I，F），其中，Q 为有限状态集合；Σ为有限字母表；I，F：Q→l为Q的ℓ－值子集，代表初始状态与接受状态；δ：Q×Σ×Q→l为ℓ－值转移函数或量子转移函数。

以下用σ表示Σ中的符号，用ω、θ表示Σ中的字符串，ε用来表示空串。为了方便，用ℓ（Σ＊）表示Σ＊上的所有ℓ－值语言之集合。对ℓ-VFA M＝（Q，Σ，δ，I，F）对应的ℓ－值可识别谓词为recM∈ℓ（Σ＊），对于输入串ω∈Σ＊，令ω＝σ1σ2…σn，有：

recM（ω）＝ （∃q0∈Q）（∃q1∈Q）…

（∃qn∈Q）（q0∈I∧qn∈F∧

（q0，σ1，q1）∈δ∧ … ∧ （qn－1，σn，qn）∈δ）即命题recM（ω）的真值定义为：

recM（ω） ＝∨ ｛I（q0）∧δ（q0，σ1，q1）∧ … ∧

δ（qn－1，σn，qn）∧F（qn）：q0，…，qn∈Q｝

对L∈ℓ（Σ＊），若存在ℓ-VFA使得L＝recM，则称L为Σ＊上的ℓ－值正则语言。

引理1［15，17］设ℓ为一个格，X 为ℓ的有限子集，则由X生成的ℓ的∧－半格X∧与∨－半格X∨都是有限的，而且：

X∧＝ ｛x1∧x2∧ … ∧xk：x1，x2，…，xk∈X，k≥1｝∪ ｛1｝

X∨＝ ｛x1∨x2∨ … ∨xk：x1，x2，…，xk∈X，k≥1｝∪ ｛0｝

文献［15］给出了一种限制了的ℓ-VFA，该定义与文献［12］定义的确定型ℓ－值自动机有着明显的不同。

定义2［15］ℓ－值确定型有穷自动机（简记为ℓ-VDFA）是五元组 M ＝ （Q，Σ，δ，q0，F），其中，Q为有限状态集；Σ为有限字母表；q0∈Q是初始状态；F为Q的ℓ－值子集，代表终状态；δ：Q×Σ→Q为状态转移函数。

对ℓ-VDFA M ＝ （Q，Σ，δ，q0，F），对应的ℓ-值可识别谓词recM∈ℓ（Σ＊），对输入串ω∈Σ＊，令ω＝σ1σ2…σn，

recM（ω）＝ （∃q0∈Q）（∃q1∈Q）…（∃qn∈Q）（qn∈F∧δ（q0，σ1）＝q1∧ … ∧δ（qn－1，σn）＝qn）

则命 题recM的 真 值 定 义 为 recM（ω） ＝F（δ＊（q0，ω））。

引理2［15］对任意ℓ-VFA M ＝ （Q，Σ，δ，I，F），存在ℓ-VDFA Md＝ （Qd，Σ，η，q0，E）与 M 等价，即recM＝recMd。

定义3 ℓ－值正则文法G（简记为ℓ-RG）是一个四元组G＝ （ N，Σ，P，S ） ，其中N为非终止符的非空有限集，Σ是终止符的非空有限集，且N∩Σ＝Ø，而I：N→l，即N的ℓ－值子集（量子开始符号）。命题“S为开始记号”，记为S∈I，真值为I（S），P＝ ｛ A →ρx：A∈N，x∈ΣB，B∈N ∪｛Λ｝或A ＝ S，x＝Λ，ρ∈l－ ｛0｝｝，且P 的 支集Supp（P）有限，表示ℓ－值产生式的有限集合，其中A→ρx被解释为变元A可被替换为任意字符串x的真值为ρ，即 A→x ＝ρ。

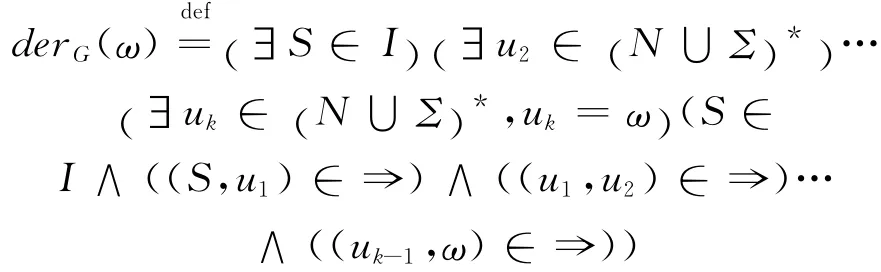
则命题derG（ω）的真值定义为：

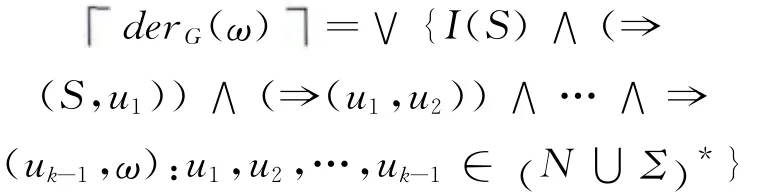
此时，derG称为ℓ－值正则文法G生成Σ＊上的ℓ－值正则语言。同样地，对任意L∈ℓ（Σ＊），若存在ℓ-RG G使得L＝derG，则称L为Σ＊上的ℓ－值正则语言（或称量子正则语言）。

对任一ℓ-RG G＝ （ N，Σ，P，I） ，G生成的量子正则语言derG作为Σ＊到l的函数，其像集：Im （de rG） ＝ ｛ r∈l：∃ω ∈Σ＊，derG（ω） ＝r｝是derG（ω）的有限子集。

由上述讨论可知，对任一ℓ-RG来说，它产生的语言的像集总是有限的，所以在讨论ℓ-RG的过程中，虽然格ℓ可能是无限的，但对于ℓ-RG G来说，它产生的语言的真值只取ℓ中的有限子集，因此总可以假设ℓ为有限的正交模格，从而可以简化讨论。而对于ℓ为无限的正交模格的情形，以下讨论都是成立的。

在基于量子逻辑的自动机理论中，很多重要的定理成立都必须依赖于正交模格中子集的交换子的条件来保证，特别地，在量子逻辑的情况下，ℓ－值正则语言对于语言的交、补、Kleene闭包运算并不封闭，所以文献［12］给出了一些条件，包括交换子分配律的条件，来保证这些运算的封闭性。文献［15］定义了ℓ－值有穷自动机（ℓ-VFA）和ℓ－值确定型有穷自动机（ℓ-VDFA），并通过广义子集构造，证明了它们是等价的。ℓ-VFA与ℓ-VDFA等价性还表明量子逻辑下的有穷自动机可以处理量子语言，但它们在处理的过程中直接使用经典有穷自动机的相关技术。需要注意的是，ℓ-VFA转化ℓ-VDFA，复杂性会增加，但对于ℓ－值正则语言对于语言的交、补、Kleene闭包封闭性的讨论带来了极大方便。

定义6 ℓ－值确定型正则文法（简记为ℓ-DRG）是一个四元组G＝ （N，Σ，P，I），其中N 为有限非终止符集；Σ为有限终止符集；I为N的ℓ－值子集，代表开始符号；而这里的ℓ－值产生式P为如下形式：

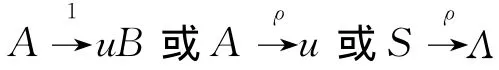
其中A、B∈N，u∈Σ，ρ∈l－｛0｝。显然，ℓ-DRG是一种特殊的ℓ-RG。

对ℓ-DRG G＝ （N，Σ，P，I），定义在Σ＊上的一元ℓ－值可产生的谓词dderG，对于任意ω∈Σ＊，有：

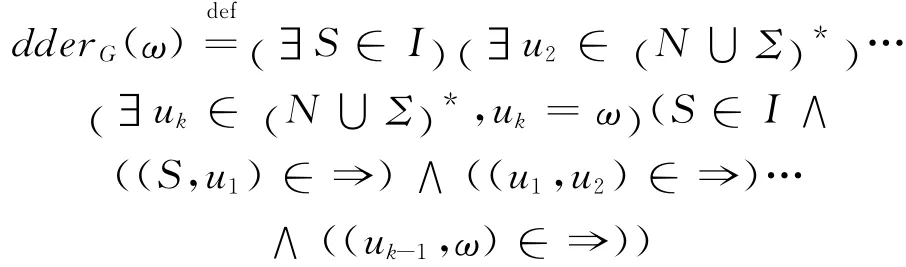
则命题dderG（ω）的真值定义为：

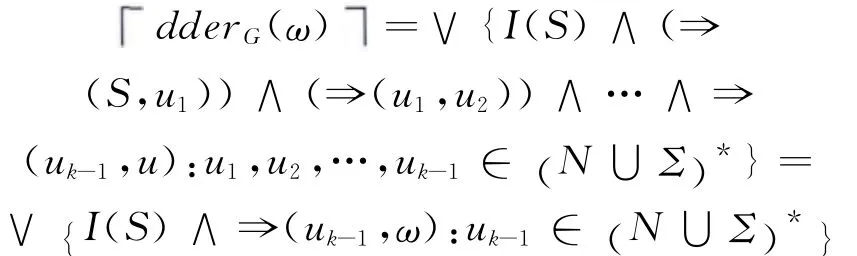
对任意L ∈ℓ（Σ＊），若存在ℓ-DRG G 使得L＝dderG，则称L为Σ＊上的量子确定正则语言（ℓ－值确定正则语言）。

定理1 设G＝ （N，Σ，P，I）为任一ℓ-DRG，则存在ℓ-VDFA M使得对任意ω∈Σ＊，有：

即recM＝dderG。

其中ρZk为某个状态Zk所对应的产生式的真值。

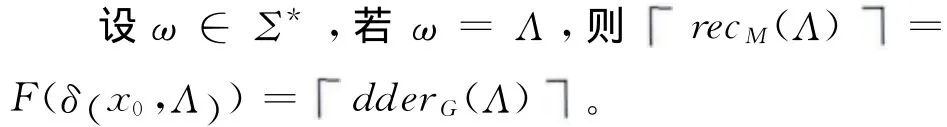
而对ω ≠Λ，令ω ＝u1u2…un－1un，则存在S∈I，使得在ℓ-DRG G中的推导链为：

1.2.1 对照组 常规护理，包括术前访视、术前准备、入室的安抚、麻醉护理、体位管理、医护配合，对于冲洗液需要控制好温度。术中密切监测患者的生命体征，出现异常，遵医嘱给予静脉用药等干预，纠正呼吸循环紊乱。出现术中出血等并发症，配合医师做好救治。糖尿病对象，需要在术前确认血糖控制情况，胰岛素控制血糖的疗效。血糖达标的对象常规口服二甲双胍和（或）阿卡波糖控制血糖，高血糖（＞8.3 mmol/L)的对象给予胰岛素控制血糖，低血糖（＜5.1 mmol/L）输液纠正，将血糖控制在5.6～11.2 mmol/L。

定理 2 设 M ＝ （Q，Σ，δ，x0，F）为 任 一ℓ-VDFA，则存在ℓ-DRG G使得对任意ω ∈Σ＊，有：

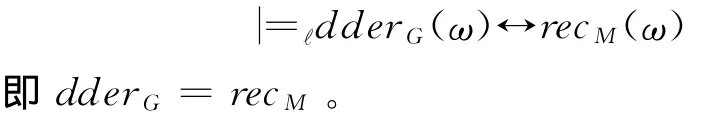
证明 设 M ＝ （Q，Σ，δ，x0，F）为一ℓ-VDFA，现构造一个ℓ-DRGG＝ （N，Σ，P，I）如下：

根据上述两个结论，我们得到下面的结论：

定理3 对有限集Σ上的量子语言L，L被一个ℓ-DRGG产生当且仅当L被一个ℓ-VDFA M识别。

根据上述讨论，ℓ-DRG产生的ℓ－值确定正则语言与ℓ-VDFA识别的量子语言等价，进一步可以证明ℓ-RG 与ℓ-VFA 是等价的，而ℓ-VFA 又与ℓ-VDFA是等价，并根据引理1，可以验证基于量子逻辑的确定型正则文法和量子正则文法是等价的。

定理4 设ℓ为一完备正交模格，X为ℓ的任意有限子集，如果由X生成的子代数是有限集，则对任意ℓ-RGG，都存在一个与其等价的ℓ-DRG G′，即dderG′＝derG。

3 ℓ－值确定型正则文法的性质

引理2 设量子文法G1＝ （N，Σ，P，I），I为N 的ℓ－值子集，代表开始符号，而这里的ℓ－值产生式P只有形式为A→1uB ，其中B∈N∪｛Λ｝，u∈Σ，其产生的量子语言定义为：

这类ℓ－值量子文法与ℓ-DRG是等价的。

定理5 设L：Σ＊→l为ℓ－值量子语言，以下条件等价：

（1）存在ℓ-DRG G，使得L＝dderG；

（2）存在k1，k2，…，kn∈ l－｛0｝，及正则语言L1，L2，…，Ln使得L＝∨in＝1ki1Li，其中1Li表示Li的特征函数；

（3）存在k1，k2，…，kn∈ l－｛0｝，及两两不交的正则语言L1，L2，…，Ln使得L ＝ ∨in＝1ki1Li。

证 明 （ 1）⇒（3）：设 L 由 ℓ -DRG G ＝（N，Σ，P，I） 产生，则对任意ω∈Σ＊，根据引理2，存在与之等价量子文法G1＝ （ N1，Σ，P1，I1），并且有 derG1（ω） ＝ ∨S∈I1｛I1（S）S⇒＊ω｝。设Im（I1） － ｛0｝＝ ｛k1，k2，…，kn｝ ，令 I（i）＝｛S ∈ N1：I1（S）＝ki｝ ，由 此 构 造 的 文 法 G（i）＝（N，Σ，P（i），I（i）） 为经典的文法，其中P（i）为P1去真值所对应的经典产生式的集合。设该文法产生的语言为Li，根据构造知，Li为正则语言且｛Li｝in是两两不相交的。

因此，ω∈Li当且仅当S⇒＊ω且S∈I（i），由此可知，

（3）⇒（2）：显然。

（2）⇒（1）： 设 Li被 正 则 文 法 Gi＝（Ni，Σ，Pi，Si） 产生，且当i≠j时，Ni∩Nj＝Ø，i，j∈ ｛ 1，2，…，n｝。构造文法G＝ （ N，Σ，P，I）如下：N＝∪in＝1Ni，对于Pi中的产生式A→uB或者S0i→Λ∈Pi，其中B∈N∪｛Λ｝，便将这些产生式赋真值为1放入P 中，并令I（A）＝由引理2，存在与之等价的ℓ-DRG G′，使得derG′

定理6 设L：Σ＊→l为量子语言，以下命题等价：

（1）存在ℓ-DRG G，使得L＝dderG。

（2）集合Im（L）为有限集，且对任意的k∈l－｛｝0，L的r-层集，L［k］＝｛ω∈Σ＊：L（ω）＝k｝是Σ 上的正则语言，且 L ＝dderG＝ ∨k∈l－｛0｝k1L［k］，其中1L［k］表示L［k］的特征函数。

（3）集合Im（L）为有限集，且 ∀a∈l－｛0｝，A［a］为正则语言。

关于ℓ－值语言的运算如下：对任意A，B∈ℓ（Σ＊）以及r∈l，并A∨B，交A∧B，补A⊥，数量积rA，连接AB，Kleene闭包A＊定义为，对任意ω∈Σ＊，

A∨B（ω）＝A（ω）∨B（ω）；

A∧B（ω）＝A（ω）∧B（ω）；

A⊥（ω）＝A（ω）⊥；

rA（ω）＝r∧A（ω）；

AB（ω）＝∨ ｛A（ω1）∧B（ω2）：ω1ω2＝ω｝；

A＊（ω）＝∨ ｛A（ω1）∧ … ∧A（ωn）：n≥1，ω1…ωn＝ω｝。

定理7 ℓ－值确定正则语言关于ℓ－值语言的有限并、有限交、数量积、补运算、连接运算、Kleene闭包运算封闭。

定理8 设f：Σ＊1→Σ＊2为同态映射，若L为ℓ－值确定正则语言，则f－1（L）也是ℓ－值确定正则语言。

说明：定理7与定理8的证明类似于文献［15］的证明。

4 结束语

本文利用语义分析方法进一步研究了基于量子逻辑的确定型正则文法理论，证明了量子逻辑意义下的确定型正则文法与确定型有穷自动机的等价，讨论了量子逻辑意义下的正则文法可以通过经典正则文法与量子开始符号来实现，这对讨论量子逻辑下的文法带来了方便，从复杂性角度来分析，也是易行的。

［1］ Hopcroft J E，Ullman J D.Introduction to automata theory，languages and computation［M］.New York：Addison-Wesley，1979.

［2］ Zadeh L A.Outline of a new approach to the analysis of complex systems and decision processes［J］.IEEE Transactions on Systems，Man，and Cybernetics，1973（1）：28-44.

［3］ Mordeson J N，Malik D S.Fuzzy and languages：Theory and applications［M］.London：Chapman ＆Hall／CRC，2002.

［4］ Sheng L，Li Y M.Regular grammars with truth values in lattice-monoid and their languages［J］.Soft Computing，2006（10）：79-86.

［5］ Chen Bing，Zhou Zu-de，Chen You-ping，el al.Schedulability analysis of the CAN network using timed automata［J］.Computer Engineering ＆ Science，2006，28（9）：25-27.（in Chinese）

［6］ Moore C，Crutchfield J P.Quantum automata and quantum grammars［J］.Theoretical Computer Science，2000，237（1-2）：275-306.

［7］ Gudder S.Basic properties of quantum automata［J］.Foundation of Physics，2000，30（2）：301-319.

［8］ Shor P W.Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer［J］.SIAM Journal on Computing，1997，26（5）：1484-1509.

［9］ Grover L K.Quantum mechanics helps in searching for a needle in a haystack［J］.Physical Review Letters，1997，79（2）：325-328.

［10］ Ying M S.Automata theory based on quantum logic（I）［J］.International Journal of Theoretical Physics，2000，39（4）：891-991.

［11］ Ying M S.Automata theory based on quantum logic（II）

［J］.International Journal of Theoretical Physics，2000，39（11）：2545-2557.

［12］ Ying M S.A theory of computation based on quantum logic（I）［J］.Theoretical Computer Science，2005，344：134-207.

［13］ Qiu D W.Automata theory based on quantum logic：Some characterizations［J］.Information and Computation，2004，190：179-195.

［14］ Qiu Dao-wen.Automata and grammars theory based on quantum logic［J］.Journal of Software，2003，14（1）：23-27.（in Chinese）

［15］ Li Yong-ming.Finite automata based on quantum logic and monadic second-order quantum logic［J］.Science in China Series F：Information Sciences，2010，53（1）：101-114.

［16］ Han Zhao-wei，Li Yong-ming.Pushdown automata and context-free grammars based on quantum logic［J］.Journal of Software，2010，21（9）：2107-2117.（in Chinese）

［17］ Li Y M.Free semilattices and strongly free semilattices generated by partially ordered sets［J］.Northeastern Mathematical Journal，1993，9（3）：359-366.

附中文参考文献：

［5］ 陈冰，周祖德，陈幼平，等.基于时间自动机的CAN网络可调度性分析［J］.计算机工程与科学，2006，28（9）：25-27.

［14］ 邱道文.基于量子逻辑的自动机和文法理论［J］.软件学报，2003，14（1）：23-27.

［16］ 韩召伟，李永明.基于量子逻辑的下推自动机与上下文无关文法［J］.软件学报，2010，21（9）：2107-2117.