移动传感器网络区域覆盖快速检测的拓扑方法研究＊

2013-05-08易东云

计算机工程与科学 2013年9期

洪峰，刘旭，易东云

（国防科学技术大学理学院，湖南长沙410073）

1 引言

无线传感器网络 WSN（Wireless Sensor Network）是由大量廉价传感器节点通过自组织形式组成的网络系统。由于无线传感器网络组成的分布式系统广泛而潜在的应用前景，包括用于国防监控、环境监测、矿区救险以及医疗和交通等各种领域，吸引了很多研究者的研究兴趣［1～5］。无线传感器的一个显著特点是体积小、能耗较低，通过大量的传感器组成密集型的大规模网络去完成特定的任务。覆盖是衡量其工作性能的重要指标，通过研究传感器覆盖问题可提高传感器网络服务质量。当网络部署完毕后，如何评价或动态监测传感器网络对目标区域的覆盖性能是一个基本但亟待解决的问题［6，7］。由于受到价格成本和自身体积的限制，传感器节点的事件处理能力、通信带宽以及电源能量等资源极为有限。因此，研究在有限的信息条件下，快速有效地确定传感器网络对目标区域的覆盖情况具有重大意义。

本文考虑区域覆盖问题，给定一个区域，要求在任意时刻传感器网络可监控到该区域的所有子区域。区域覆盖往往出现在气候监测、森林防火等应用场景中［8］。区域覆盖的典型特征是有明确的边界，以森林火灾监测为例，可以假设边界节点是固定的，而内部节点则由于动物移动等干扰会出现一定的位置偏差。因此，其内部区域的覆盖往往存在不确定性，需要实时快速确定覆盖漏洞。本文考虑简单传感器，针对特定的检测任务配备了相应的感知原件，同时，每个传感器以一定的频率和周围节点通信。为简单起见，可假设通信距离和感知半径成一定比例关系，满足三角形覆盖条件，即按照通信距离两两相邻的三个传感器可以完全覆盖其连线围成的三角形区域。据此我们可以利用拓扑方法快速判定传感器的覆盖情况，可以从硬件设计上略去传感器的地理信息装置，如GPS定位仪。由于维持和交流额外的地理信息需要专门的硬件模块支持，且消耗有限的能源［9］，因此无需地理信息的漏洞检测算法有助于简化传感器设计，提高系统可靠性和降低制造成本。

2 相关工作

无线传感器网络的布局及覆盖问题的研究在国内外引起了极大的研究兴趣，现将简要介绍与本文相关内容。

文献［6］结合区域封闭性和计算几何的相关知识来解决无线传感器网络覆盖度判定问题。文献［8］利用贪心算法和几何理论研究了优化覆盖问题，通过节点状态调度机制转换提高节点覆盖性能，同时减少能量消耗。虚拟力算法［10］把每个节点看作一个虚拟的带电粒子，用物理学原理对节点布局，使网络覆盖区域最大化。在全局占领映射图［11］中，每一个节点都能知道全局或局部的占领映射图，据此进一步可以得到Voronoi图和Delaunay三角剖分图两类算法［4，5，12］。该方法的不足之处在于对传感器节点的感知能力的要求较高，且覆盖检测涉及繁复的几何计算。文献［13］利用不相交覆盖集连续重组方法对覆盖区域重新划分的方式研究冗余覆盖的降低，以减少能量消耗。文献［14］研究了如何减少簇头节点失效对覆盖的影响，利用pLEACH算法对覆盖区域进行合理划分，然后在每个区域内选择簇头节点，以有效地延长网络生命周期。文献［15］研究了基于边界收缩的虚拟力算法，用于传感器网络的自动布局。

上述方法在计算覆盖情况时的共同特点是利用节点的准确位置，通过计算几何的方法探测覆盖盲区，具有较高的计算复杂度。此外，传感器节点需要提供精确的地理信息，而地理位置信息的获取需要节点装备GPS定位设备或者部署大量用于定位的信标节点，在一定程度上增加了设计及制造成本。

3 基于单纯同调群的覆盖检测方法

拓扑数据分析［16］是将拓扑工具用于数据分析和处理的一项技术，它主要对数据内蕴的拓扑特性建模，通过代数拓扑的手段揭示数据的本质结构。传感器网络的覆盖问题可以抽象为一个拓扑数据分析问题，将覆盖漏洞检测等价于网络拓扑的一维代数同调群的计算问题。

假定传感器的探测半径为rc，通信半径为rb，且满足rc≥rb／3。此时任意三个传感器A、B和C，只要满足两两距离小于rb，则它们围成的三角形区域将被完全覆盖，如图1所示。

Figure 1 Theory of triangle coverage图1 三角形区域覆盖原理

这个事实可以简单证明如下：不妨设rb≥BC≥AB≥AC 。现以BC为弦，以BC中垂线A点所在一侧距离BC为3／3BC 的O点为圆心作圆，此时有 ∠BOC＝ ∠BOM ＝ 120°，其中M是BC中垂线延长后与圆O的交，如图2所示。以下证明A点将被圆O覆盖。否则，A点一定在圆O外。

由于AB≥AC ，此时AB一定与圆O交于圆弧MC上的某点，不妨设为D点。此时一定有 ∠BOD ≥ ∠BOM ＝ 1 20°，因此BD≥BC ，导致AB≥BC ，这与rb≥BC≥AB≥AC 矛盾。

Figure 2 Diagrammatic sketch of proving图2 证明示意图

于是，以A、B和C为圆心，以BO 为半径的三个圆的并将完全覆盖三角形ABC。而BO＝论。有了上述结果，我们就无需考虑三个节点的详细相对位置，测量它们的两两距离即可判定它们对三角形区域的覆盖情况。

以森林防火问题为例，由于森林有固定的边界，本文也假设传感器网络探测区域的边界是固定的。首先，边界上部署了相邻距离不超过rb的若干个传感器，这样边界上的传感器可以互相通信。然后，在探测区域内部随机地或者规则地部署传感器，传感器节点为顶点，两个传感器能够互相通信则构成边。若整个探测区域被边长不超过rb的三角形所剖分，则整个区域将被完全覆盖，即没有覆盖盲区。若某个节点不能正常工作，则无法与其他能与之通信的节点构成边，这样就可能会出现覆盖盲区。设网络的通信拓扑图为G，由于传感器的通信半径为rb，只需检查G是否全由三角形张成即可，这样完全省去了计算几何的处理过程，大大提升了计算速度。

由于三角形可以自然地扩张为一个二维的Vietoris-Rips复形［17，18］，因此可以通过计算网络通信关系拓扑的二阶单纯同调群［12］的生成元的个数来判断G对目标区域的覆盖情况。简单地说，一阶单纯同调群的生成元的个数就是覆盖漏洞的个数。如果G的一阶单纯同调群的生成元的个数大于零，便可以立即判断传感器网络存在覆盖盲区。文献［18］给出了一般情况下的单纯同调群的生成元的计算方法，这里使用的是它的一个特例。

4 实验结果与分析

应用如上的方法利用Java进行仿真实验。我们做了四组实验，分析以随机、正方形网格、三角形网格以及规则的方式部署传感器节点的网络覆盖情况。按照网格的方式部署的传感器初始时刻能够完全覆盖关注区域，正如实际检测时可能遇到的情况一样，随后对初始部署位置进行一定的扰动，这时传感器的相对位置发生一定的变化，有可能出现覆盖漏洞，然后用本文方法进行漏洞检测，快速生成结果。

为简单起见，假设探测区域是边长为100m的正方形区域，尽管我们的方法对区域的形状并不敏感。设节点的感知半径为rb。

4.1 随机部署

在边界固定生成40个传感器节点（即边界上每隔10m有一个传感器），第一组实验在正方形区域内部随机部署100个传感器节点，第二组随机部署200个传感器节点，如表1所示。

Table 1 Blind zone detection of random distribution表1 随机部署传感器网络的漏洞检测

从表1中可以看出，由于节点的分布不规则、不均匀，随机部署的传感器网络，很容易出现覆盖盲区。而且还可以看出，随着传感器节点数目的上升，覆盖盲区得到明显的改善；随着感知半径的增加，覆盖盲区也会呈现减少趋势，直至消失。

4.2 正方形网格部署

按照正方形网格部署传感器网络，网格间隔为10m，一共可部署121个传感器节点，如图3所示。

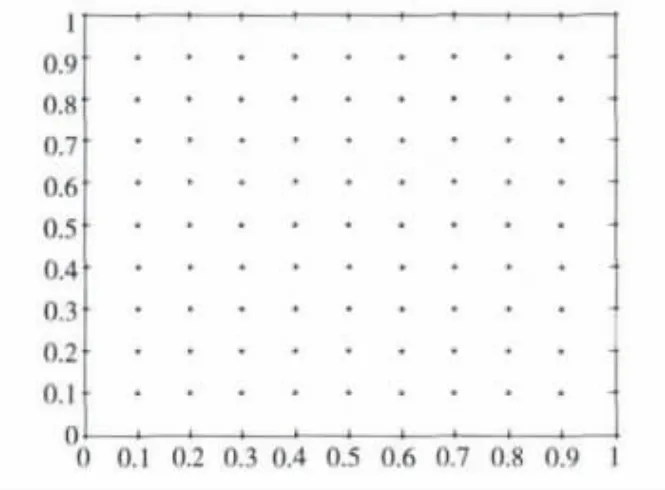
Figure 3 Square distribution图3 正方形网格部署

随后给予不同程度的扰动，给每个点的坐标加入随机扰动。第一组扰动为零，第二组和第三组的扰动量分别为1m和2m，所产生的影响如表2所示。

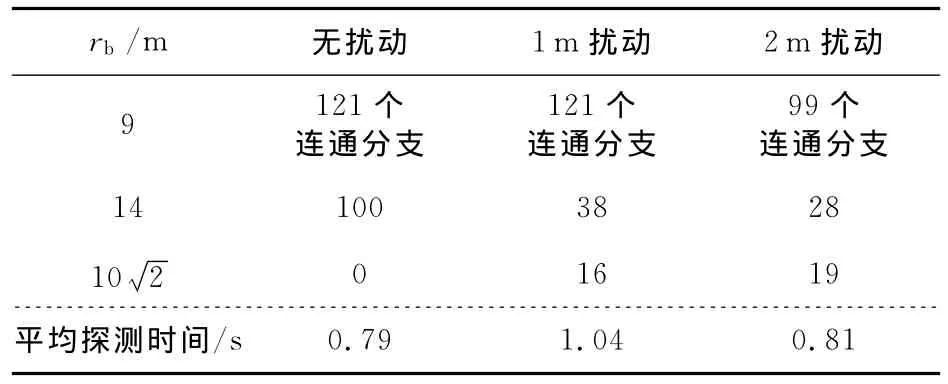
Table 2 Blind zone detection of square distribution表2 正方形网格部署的传感器网络漏洞检测

因为节点的间隔为10m，则当rb＜10时，无扰动的情况下传感器无法形成网络，是121个孤立的节点；当rb＝ 1 0 2时，无扰动的网格部署恰好完全覆盖目标区域。因此，当rb＝14时，小于上述临界值，恰好有100个覆盖漏洞，尽管每个漏洞的规模很小。于是，当增加少许的扰动后，扰动越大，覆盖漏洞数反而越少，但这是以若干较大的漏洞的出现为代价的。

4.3 三角形网格部署

用等边三角形对目标区域做完全剖分，三角形边长为10m，共部署149个传感器节点。由于是在固定的正方形区域内，我们保证区域内部的点均构成等边三角形，而将那些本应在区域外部的点置于边界上，如图4所示。

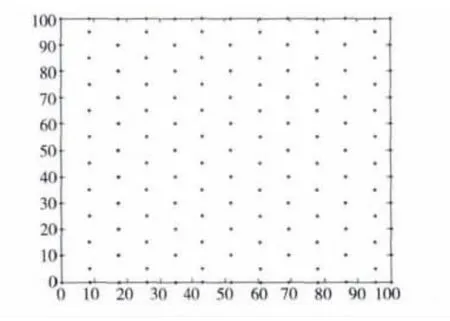
Figure 4 Triangle distribution图4 三角形网格部署

此时传感器密度高于正方形网格部署。随后给予和正方形网格部署时类似的扰动，所产生的影响如表3所示。

Table 3 Blind zone detection of triangle distribution表3 三角形网格部署的传感器网络漏洞检测

当感知半径为9m时，除边界上的一些点外，大部分点均为孤立节点。因为三角形网格的边长是10m，所以当感知半径为10m时，无扰动的一组恰好完全覆盖目标区域，而对于1m扰动的情况，出现了17个漏洞，即覆盖盲区，对于2m扰动的情况，直接将覆盖区域分成了两个不连通的区域。

4.4 规则部署

前三组实验验证了本文所提方法的有效性：在探测距离没有达到部署设定的临界值时，大部分传感器都是孤立的节点，当探测距离等于临界值时，恰好完全覆盖整个探测区域；加入扰动之后，传感器的位置发生变化，可能会出现覆盖盲区，本文提出的方法快速地检测出了盲区，并且符合实际的情况。

本小节针对4.2节和4.3节所述的规则部署区域，人为地去掉某些传感器来模拟实际中传感器失效的情况，以验证利用单纯同调群是否能够快速地检测出漏洞。对于正方形和三角形网格部署，在恰好完全覆盖的情况下，随机删除5个、10个、20个传感器节点，检验该方法能否快速且正确地检测出漏洞，所得结果如表4所示。

Table 4 Blind zone detection after deleting nodes表4 删除节点后的漏洞检测

由表4可以看出，当去掉某些传感器节点时，传感器网络出现漏洞。本文所提方法确实探测到了漏洞的存在，且探测时间均小于1s。我们随后将去掉的传感器节点的各网络以图像的方式呈现，发现图像中显示的漏洞个数与应用本文所提方法计算所得的漏洞个数是一致的。

5 结束语

针对简单传感器网络的覆盖问题，本文提出了一种快速判定方法，它仅仅假设传感器节点的通信半径和探测半径满足一定的比例关系即三角形覆盖条件，则可根据通信拓扑迅速判定传感器网络对目标区域的覆盖情况。证明了三角形覆盖条件的必要性，并用仿真实验验证了所提方法的有效性。该方法不需要知道传感器节点的完整地理信息，从而大大降低了对传感器设计和制造的要求，并有利于提高传感器的能效和网络可靠性。

［1］ Chen Lin-xing.Technology and application of wireless sensors network［M］.Beijing：Electronic Industry Publisher，2009.（in Chinese）

［2］ Ma Zu-chang，Sun Yi-ning，Mei Tao.Summary of wireless sensors network［J］.Journal of China Institute of Communications，2004，25（4）：114-124.（in Chinese）

［3］ Tamboli N，Younis M.Coverage-aware connectivity restoration in mobile sensor network［J］.Journal of Network and Computer Applications，2010，33（4）：363-374.

［4］ Lu Ke-zhong，Chen Guo-liang，Feng Yu-hong.Approximate algorithm of the minimum relaying nodes of wireless sensors network［J］.Chinese Science：Information Science，2010，40（11）：1473-1482.（in Chinese）

［5］ Carbunar B，Grama A.Redundancy and coverage detection in sensor networks［J］.ACM Transactions on Sensor Networks，2002，2（1）：94-128.

［6］ Fan Gao-jun，Jin Shi-yao.An algorithm for evaluating the coverage degrees of the wireless sensor network with arbitrary sensing areas［J］.Computer Engineering ＆ Science，2010，32（10）：12-15.（in Chinese）

［7］ Tao Dan，Ma Hua-dong，Liu Liang.A virtual potential field based coverage-enhancing algorithm for directional sensor networks［J］.Journal of Software，2007，18（5）：1152-1163.（in Chinese）

［8］ Wang Wei，Lin Feng，Zhou Ji-liu.Research progress on coverage problem in wireless sensor networks［J］.Application Research on Computer，2010，27（1）：32-35.（in Chinese）

［9］ Liu Ming，Cao Jian-nong，Zheng Yuan，et al.Analysis for multi-coverage problem in wireless sensor networks［J］.Journal of Software，2007，18（1）：127-136.（in Chinese）

［10］ Khatib Q.Real-time obstacle avoidance for manipulators and mobile robots［J］.International Journal of Robotics Research，1986，5（1）：90-98.

［11］ Liu Ben-yuan，Towsley D.A study of the coverage of large scale sensor networks［C］∥Proc of 2004IEEE International Conference on Mobile Ad-Hoc and Sensor System，2004：475-483.

［12］ Xu Peng-fei，Chen Zhi-gang，Deng Xiao-heng.Distributed Voronoi coverage algorithm in wireless sensor networks［J］.Journal of Communication，2010，31（8）：16-25.（in Chinese）

［13］ Zhang H，Hou J C.Maintaining sensing coverage and connectivity in large sensor networks［J］.Wireless Ad Hoc and Sensor Networks：An International Journal，2005，1（1-2）：89-123.

［14］ Gao Tie-gang，Niu Wei-wei.A cluster head election algorithm based on the coverage of nodes［J］.Computer Engineering ＆Science，2011，33（5）：1-8.（in Chinese）

［15］ Zhang Ying，Guo Peng，Zhou Zong－yi.Research on the coverage algorithms for mobile sensor networks［J］.Computer Engineering ＆ Science，2008，30（2）：81-83.（in Chinese）

［16］ Carlsson G.Topology and data［J］.Bulletin（New Series）of the American Mathematical Society，2010，46（2）：255-308.

［17］ Chambers E W，de Silva V，Erickson J，et al.Vietoris-rips complexes of planar point sets［J］.Discrete Comput Geom，2010，44（1）：75-90.

［18］ Zomorodian A.Computational topology［M］∥Algorithms and Theory of Computation Handbook.Second Edition，2009.

附中文参考文献：

［1］陈林星.无线传感器网络技术与应用［M］.北京：电子工业出版社，2009.

［2］马祖长，孙怡宁，梅涛.无线传感器网络综述［J］.通信学报，2004，25（4）：114-124.

［4］陆客中，陈国良，冯禹洪.无线传感器网络最小中继节点问题的近似算法［J］.中国科学：信息科学，2010，40（11）：1473-1482.

［6］范高俊，金士尧.任意感知模型的传感器网络覆盖度判定算法［J］.计算机工程与科学，2010，32（10）：12-15.

［7］陶丹，马华东，刘亮.基于虚拟势场的有向传感器网络覆盖增强算法［J］.软件学报，2007，18（5）：1152-1163.

［8］王伟，林锋，周激流.无线传感器网络覆盖问题的研究进展［J］.计算机应用研究，2010，27（1）：32-35.

［9］刘明，曹建农，郑源，等.无线传感器网络多重覆盖问题分析［J］.软件学报，2007，18（1）：127-136.

［12］徐鹏飞，陈志刚，邓晓衡.无线传感器网络中的分布式Voronoi覆盖控制算法［J］.通信学报，2010，31（8）：16-25.