A nearest neighbor search algorithm of high-dimensional data based on sequential NPsim matrix①

Li Wenfa (李文法):Wang Gongming :Ma Nan:Liu Hongzhe

(*Beijing Key Laboratory of Information Service Engineering，Beijing Union University，Beijing 100101，P.R.China)(**National Laboratory of Biomacromolecules:Institute of Biophysics:Chinese Academy of Sciences:Beijing 100101:P.R.China)



A nearest neighbor search algorithm of high-dimensional data based on sequential NPsim matrix①

Li Wenfa (李文法)*To whom correspondence should be addressed.E-mail:liwenfa@buu.edu.cnReceived on Dec.16，2015*:Wang Gongming**:Ma Nan*:Liu Hongzhe*

(*Beijing Key Laboratory of Information Service Engineering，Beijing Union University，Beijing 100101，P.R.China)(**National Laboratory of Biomacromolecules:Institute of Biophysics:Chinese Academy of Sciences:Beijing 100101:P.R.China)

Problems existin similarity measurement and index tree construction which affect the performance of nearest neighbor search of high-dimensional data.The equidistance problem is solved using NPsim function to calculate similarity.And a sequential NPsim matrix is built to improve indexing performance.To sum up the above innovations:a nearest neighbor search algorithm of high-dimensional data based on sequential NPsim matrix is proposed in comparison with the nearest neighbor search algorithms based on KD-tree or SR-tree on Munsell spectral data set.Experimental results show that the proposed algorithm similarity is better than that of other algorithms and searching speed is more than thousands times of others.In addition:the slow construction speed of sequential NPsim matrix can be increased by using parallel computing.

nearest neighbor search:high-dimensional data:similarity:indexing tree:NPsim:KD-tree:SR-tree:Munsell

0 Introduction

The nearest neighbor search is looking for several points that are nearest from the given point[1]:which is widely used in text clustering:recommendation system:multimedia retrieval:sequence analysis:etc.Generally speaking:the data whose dimensionality is more than 20 belongs to high-dimensional data[2].The traditional nearest neighbor search algorithms may fail in high-dimensional data because of the curse of dimensionality[3].Thus:the nearest neighbor search of high-dimensional data has become a challenging but useful issue in data mining.Currently:this issue has been researched to a certain extent.With position sensitive hashing algorithm[4]:a high-dimensional vector is mapped onto address space:and previous similar points are still close to each other in a larger probability:which overcomes the equidistance of high-dimensional data.But its applicability is limited because of same hash functions and neglection of data difference.To solve this problem:a self-taught hashing (STH)[5]was proposed by Zhang:et al.The similarity matrix is built at first.And the matrix decomposition and eigenvalue solution are carried out subsequently.But it has large time and space complexity.The iDistance[6]and vector approximation file (VA-File)[7]are suitable for indexing structure.However:its query cost is very huge.

In essence:the similarity measurement and index tree construction have affected performance of nearest neighbor search of high-dimensional data.Thus:solving problems that exist in above aspects is very important.At present:most of similarity measurement methods of high-dimensional data ignore the relative difference of property:noise distribution:weight and other factors:which are valid for a small number of data types[8].Psim(X,Y) function considers the above factors[8]and is applicable for all kinds of data type.But it is unable to compare similarity under different dimensions because its range depends on spatial dimensionality.Thus:the NPsim(X:Y) function is proposed to solve this problem and makes its range [0:1].The defect of index tree on construction and query has made up with sequential NPsim matrix.This method is easy to parallelize.Assuming that the dimensionality is M:the time complexity of building sequential NPsim matrix is O(M2·n):but the one after parallelization is reduced into O(M·n).The time complexity of nearest neighbor search is O(1).This algorithm is compared with the nearest neighbor search algorithms based on KD-tree or SR-tree on Munsell spectral data set.The experimental results show that the similarity of our proposed algorithm is better than the one of other algorithms.The construction of sequential NPsim matrix is time consuming:but its searching speed is more than thousands times of others.In addition:the construction time of sequential NPsim matrix can be reduced dramatically by virtue of parallelization.Thus:its whole performance is better than the one of others.

1 Related work

In recent years:the similarity measurement and index tree construction have been researched to a certain extent.But insufficiency still exists.

To solve the problem in similarity measurement:the Hsim(X:Y) function[9]was proposed by Yang:which is better than traditional method:but neglects the relative difference and noise distribution.The Gsim(X:Y) function[10]is proposed according to relative difference of properties in different dimensions.But the weight discrepancy is ignored.The Close(X:Y) function[11]based on monotone decreasing of e-xcan overcome the influence from components in some dimensions whose variance are larger.But relative difference is not considered which would be affected by noise.The Esim(X:Y)[12]function is proposed by improving Hsim(X:Y) and Close(X:Y) functions.In each dimension:the Esim(X:Y) component is positive correlation to the value in this dimension.All dimensions are divided into two parts:normal dimension and noisy dimension.In noisy dimension:the noise occupies majority.When noise is similar to and larger than the one in normal dimension:this method will be invalid.The secondary measurement method[13]is used to calculate the similarity by virtue of property distribution:space distance:etc.But the noise distribution and weight have been neglected.In addition:it is time-consuming.The projection nearest neighbor is proposed by Hinneburg[14]:which is used to solve the problem in higher dimensional space by dimension reduction.But it is hard to find right quality criterion function.In high-dimensional space:Yi has found[8]that the difference in noisy dimension is larger:no matter how similar data is.This difference has occupied a large amount of similarity calculation:which results in the distances between all points to be similar.Therefore:Psim(X:Y) function[8]is proposed to eliminate the noisy influence by analyzing difference among all dimensions.The experimental result indicates that this method is suitable for all kinds of data type.But its range is [0:n]:where n is dimensionality.Thus:the similarities in different dimensions are unable to compare.

There are two kinds of index trees used in high-dimensional space:index tree based on the vector space:and index tree based on metric space.The typical example of the former is R-tree[15].It is a natural extension of B-tree in high-dimensional space and can solve the data searching problem.However:R-tree has the problems of brother node overlap:multiple queries:and low utilization:etc.Therefore:the extension of R-tree has been proposed:such as R+tree:R*tree:cR-tree.The common structure of the later is VP-tree[16]:which is a binary search tree and suitable for large-scale data search.But it is a static tree and could not be inserted or deleted.In addition:the distance calculation is time-consuming.MVP-tree is the improvement of VP-tree[17]and the cost of distance calculation is decreased.But its time complexity in stage of creation or query is higher than the one of VP-tree.M-tree is the hash index represented by B-tree[18]and has high searching efficiency.However:it can only carry out single value searching:instead of range searching.SA-tree is created according to the distance between leaf node and root node[19].But it is a completely static tree and could not be inserted or deleted.

2 Key technology

2.1 Similarity measurement

Inn-dimensional space:set S={S1:S2:…:SM} is composed of M points Si={Si1:Si2,…,Sij,…,Sin}:where i=1,2,…,M:j=1,2,…,n:and Sijis the jth property of Si.Assuming that X and Y are any two points in set S:Sim(X:Y) is similarity between X and Y.

Sim(X:Y) is usually measured with distance function.The typical methods include Manhattan distance:Euclidean distance:etc.However:with the increase of dimensionality:the nearest and farthest distances become the same[2].Thus:these methods are invalid in high-dimensional space.To solve this problem:several methods are proposed:such as Hsim(X:Y):Gsim(X:Y):Close(X:Y):Esim(X:Y):yet they are valid for limited types of data[2].The Psim(X:Y) is suitable for a variety of data type:and its range is dependent on spatial dimensionality and unable to compare the similarity under the different dimensions.Under the circumstance of maintaining effects:Psim(X:Y) is updated as

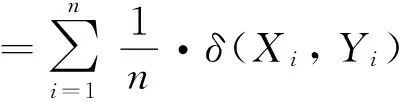
(1)

where Xiand Yiare components in ith dimension.δ(Xi:Yi) is discriminant function.If Xiand Yiare in the same interval [ni:mi]:δ(Xi:Yi)=1 is hold.Otherwise:δ(Xi:Yi)=0 is hold.E(X:Y) is the number of intervals in which components of X and Y are all the same.It can be seen that the range of NPsim(X:Y) is in [0:1].The above is the outline of NPsim:and detailed introduction can be found in reference[8].

To validate this method:several records in dimensions of 10:30:50:100:150:200:250:300:350:and 400 are generated with normrnd() function of Matlab.The number of records in every dimension is 1000.After that:relative difference between the farthest and the nearest neighbors is calculated with

(2)

where Dmaxn:Dminnand Davgnare maximal:minimal and average similarities in n-dimensional space respectively[20].

According to the characteristics of results:similarity measurement methods are divided into two kinds.The first kind of methods include Manhattan distance:Euclidean distance:Hsim(X:Y):Gsim(X:Y):Close(X:Y) and Esim(X:Y).The others include Psim(X:Y) and NPsim(X:Y).The result is shown in Fig.1.It can be seen that relative difference of the second kind of methods is two or three magnitudes than the one of the first.Therefore:the performance advantage of the second kind of methods is obvious.

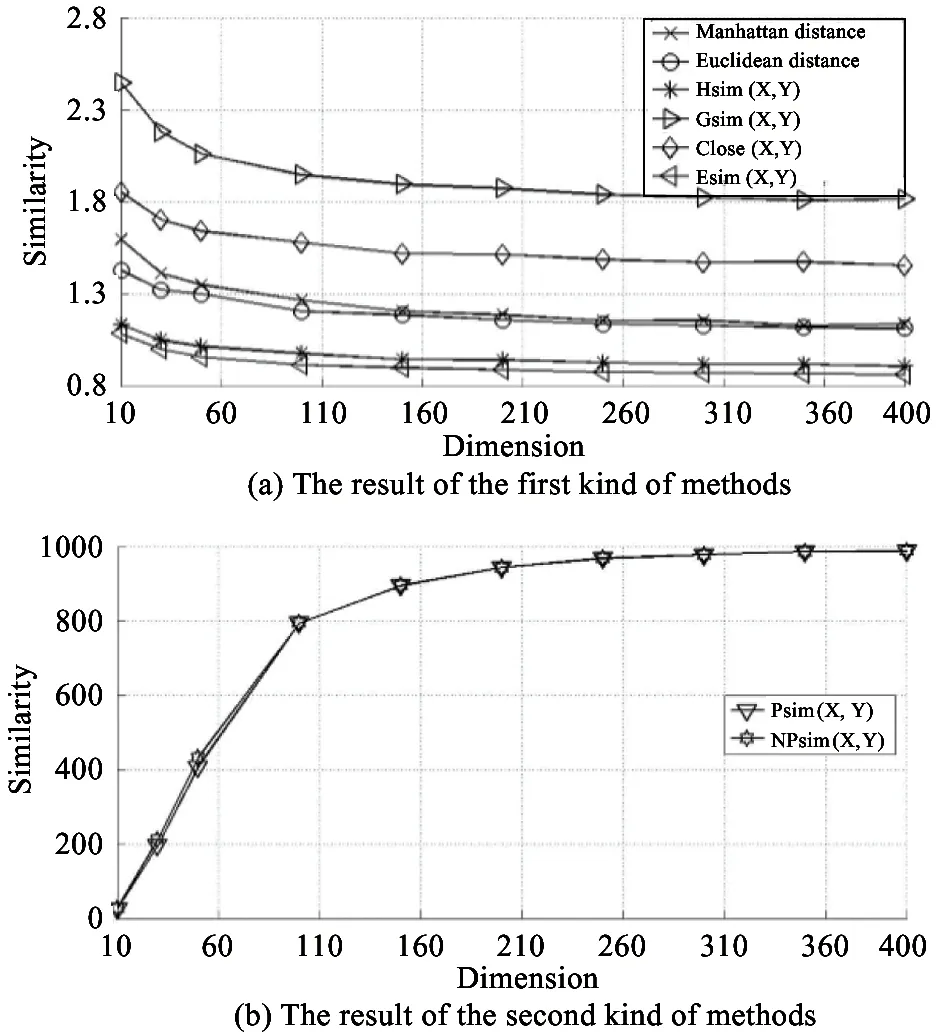
Fig.1 Relative difference of various similarity measurement methods

The numbers of Psim(X:Y)≥1 in different dimensions are shown in Table 1.The number of Psim(X:Y) in every dimension is 1000×1000=1000000.Thus:the 6%～15% result is more than 1:which is unable to compare the similarity in different dimensions.But this problem is not existed in NPsim(X:Y) function.

Table 1 Number of Psim(X:Y)>=1 in different dimensions

2.2Knearest neighbor search

For any point Stin set S:1≤t≤M:search for set Rt⊆S composed of k points:which meets the following requirements.

∀r∈Rt:NPsim(St:r)≥max{NPsim(St:s)|s∈S∩s∉Rt}

Rtis theKnearest neighbor (KNN) set of St.The course for generating Rtis called KNN search.

3 Nearest neighbor search algorithm

3.1 Whole framework

The whole framework is shown in Fig.2.First of all,NPsim matrix is generated.After that:sequential NPsim matrix produced by sorting elements in each row of NPsim is sorted in descending order.

Fig.2 Whole framework of the proposed algorithm

3.2 Execution flow

1) Construction of NPsim matrix

The NPsim matrix is generated with the following steps.

Step 1 M points Si:i=1,2,…,M are stored in M×n matrix DataSet.

Step 2 The elements in every column of DataSet are sorted in ascending order in order to generate the matrix SortDataSet.

Step 3 The elements in each column of SortDataSet are divided into G=「θ·n⎤ intervals.Thus:the number of elements in every interval is T=「M/G⎤.Meanwhile:the endpoint of every interval is saved into the matrix FirCutBound.

Step 4 The interval number of element of DataSet is determined according to the matrix FirCutBound:which is saved into the interval number matrix FirNumSet.

Step 5 The M×M matrix SameDimNum is generated.For any two points Spand Sq:the number of intervals in which components of Spand Sqare all the same is calculated and saved into the matrix element SameDimNum[p][q].

Step 6 The matrix SortDataSet is divided along the column again.The number of intervals is G′=G-1 and there are T′=|M/G′| elements in each interval.After that:the endpoint of every interval is saved into the matrix SecCutBound.

Step 7 The interval number matrix SecNumSet is produced according to Step 4.

Step 8 The matrix SameDimNum is updated.For any points Spand Sq:if the interval number of components in one dimension is different in Step 3:but same in Step 7:then SameDimNum[p][q]=SameDimNum[p][q]+1.

Step 9 The M×M matrix NPsimMat is built according to the results from Step 3 to Step 9.The NPsim information of Spand Sq(1≤p:q≤M) is stored into NPsimMat[p][q]:which includes three parts:subscript p and q:NPsim(Sp:Sq).

2) Sorting for NPsim matrix

The sequential NPsim matrix is produced with the following steps.

Step 1 The M×M matrix SortNPsimMat is produced:which is the copy of NPsimMat.

Step 2 The elements in each row of SortNPsimMat are sorted in the descending order of NPsim.

With the increase of column number:elements in pth row becomes lower and lower:which represents the distance between Spand corresponding point is farther and farther.

3) Nearest neighbor search

The KNN of Siis found out as follows.

Step 1 The frontierKelements in ith row are selected.

Step 2 The points different from Siare expected result.

3.3 Time complexity analysis

This algorithm is separated into two stages:construction of sequential NPsim matrix and searching KNN.There are two steps at the first stage:the time complexity is analyzed as follows.

(1) Construction of NPsim matrix

In this step:four kinds of matrixes are produced.The first is SortDataSet and is produced by sorting elements in every column.Its time complexity is O(MlogM·n).The second is FirCutBound and SecCutBound that are generated by visiting all elements of DataSet.Thus:the time complexity is O(M·n).The third is FirNumSet and SecNumSet which are obtained by locating the column number of element.The corresponding time complexity is O(M2·n).The fourth is SameDimNum that is produced by comparing the element per column.The time complexity of this operation is O(M2·n).Finally:the NPsim component is calculated and summed up to whole NPsim value.

(2) Sorting for NPsim matrix

The elements in every row of NPsimMat are sorted in the descending of NPsim.Its time complexity is O(M·nlogn).

To sum up above analysis:the time complexity of construction stage is O(M2·n)+O(M·nlogn)=O(M2·n).

In the course of searching:the frontierKelements in ith row are visited.Thus:the corresponding time complexity is O(1).

4 Experiment

The proposed algorithm includes two stages (construction and searching) that must be contained in the selected algorithm in comparison.For nearest neighbor search algorithm based on KD-tree:the KD-tree is built at first:and searching is carried out subsequently.The nearest neighbor search algorithm based on SR-tree is similar.Thus:the above two algorithms are selected in the following experiment.

4.1 Data introduction

The Munsell Color-Glossy set is proposed by American chromatist Munsell and is revised repeatedly by American National Standards Institute (ANSI) and Optical Society:which is one of the standard color sets and includes 1600 colors and each of them is represented with HV/C.The H:V:and C are abbreviations of hue:brightness and saturation respectively.

The spectral reflectance of all colors in Munsell Color-Glossy set is downloaded from spectral color research group (http://www.uef.fi/fi/spectral/home).Each of them is a vector that contains 401 piece of spectral reflectance in different wavelengths:which is regarded as high-dimensional data.

4.2 Overview

First of all:the running times of constructing sequential NPsim matrix:KD-tree:and SR-tree are calculated.After that:KNN search of given point in Munsell color cubic is carried out.The locations of given point and neighbors must be close or continuous.

Assuming that HV/C and HKVK/CKare given point and corresponding neighbors respectively:the Munsell distance between them is

Distance=|HK-H|+|VK-V|+|CK-C|(3)

On one hand:the neighbor colors from three algorithms are compared.On the other hand:with the increase of K:the construction and searching times of different algorithms are calculated and analyzed.

4.3 Result

The proposed algorithm:and traditional algorithms based on KD-tree and SR-tree are implemented in the experiment:and the results are compared in aspects of accuracy and speed.There is no parallel strategy used in the following experiment.The hardware includes AMD Athlon(tm) II X2-250 processor and Kingston 4G memory and the software is WinXP operation system and MicroSoft Visual Studio 2008.

1) Accuracy analysis

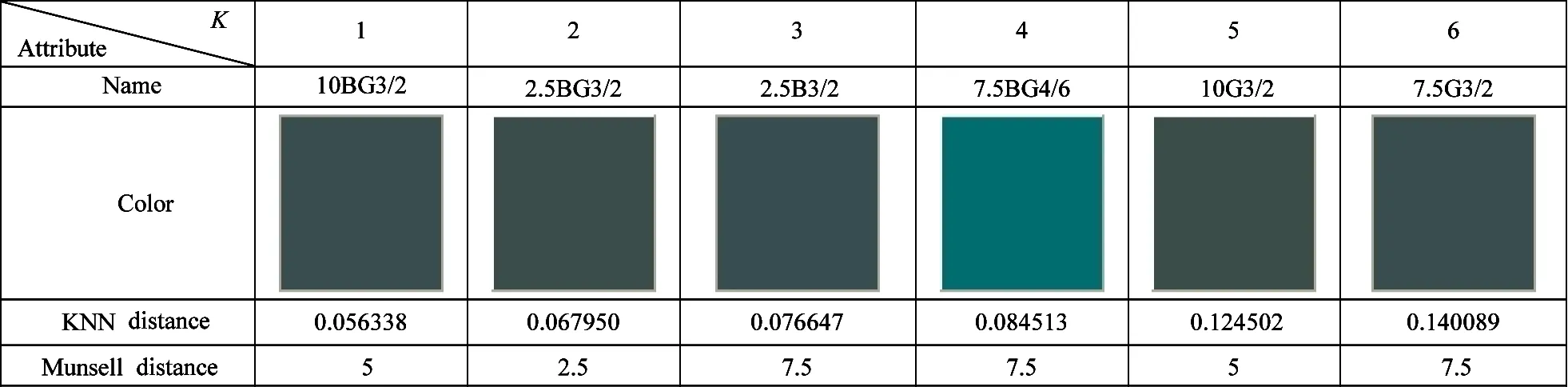
The Munsell color 5BG3/2 is selected for KNN search:which is shown in Fig.3.Searching result is shown in Table 2:3:and 4 under the circumstanceK=6.In Table 2:KNN distance is the NPsim value:and the one in Table 3 and 4 is the Euclidean distance.It can be seen that the color from the proposed method is closer to the given color.But the one from other methods has obvious difference from 5BG3/2:such as 5B3/4 in Table 3 and 7.5BG4/6 in Table 3.In addition:the Munsell distance of the proposed method is less than the one of others.In some cases:the Munsell distances of pioneers:nearest neighbors:and successors are not the ascending order:which is called as reverse phenomenon.The 10BG3/2 in Table 2:5B3/4 in Table 3:and 7.5BG4/6 in Table 4 are typical examples.The number of nearest neighbors with reverse phenomenon in Table 2:3:and 4 are 2:4:and 4:which indicates the stability of the proposed method is better than the one of others.

Fig.3 Color of 5BG3/2

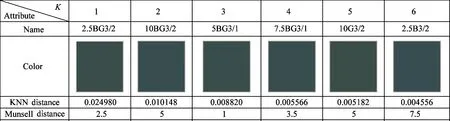
Table 3 KNN result of KD-tree algorithm

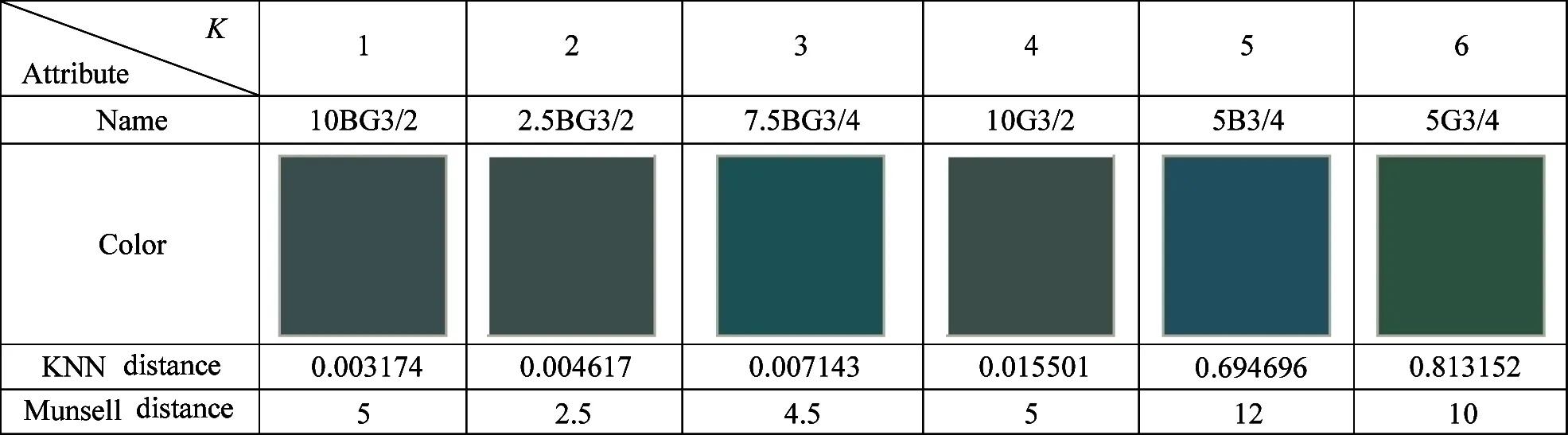
Table 4 KNN result of SR-tree algorithm

2) Speed analysis

The construction time of indexing structure is shown in Table 5.It can be seen that the one of sequential NPsim matrix is about ten times of the one of KD-tree or SR-tree.

Table 5 Construction time of different indexing structures

With the increase ofKvalue:the average searching time for KNN of 1000 selected Munsell colors are shown in Fig.4.The experimental result indicates that the magnitude of the proposed method is about 10-6:but the one of other methods is about 10-2.That is to say:the searching speed of the proposed method is more than thousands times of others.

Although the construction speed of sequential NPsim matrix is slow:the searching speed is fast.And sequential NPsim matrix can be stored into disk and loaded with high speed at any time.So:the performance of sequential NPsim matrix is better than the one of KD-tree and SR-tree in nearest neighbor search of high-dimensional data.

Fig.4 Average searching time of KNN with different algorithms

5 Conclusion

The nearest neighbor search of high-dimensional data is the foundation of high-dimensional data processing.The problem existing in the similarity measurement and index tree construction has affected the performance of traditional nearest neighbor search algorithm.The NPsim function and sequential NPsim matrix are designed to solve this problem:which are combined to propose a new nearest neighbor search algorithm.To validate the proposed algorithm:the traditional algorithms based on KD-tree and SR-tree are compared in the experiment on Munsell Color-Glossy set.The results show that the accuracy and searching speed of the method are better than the one of two methods.

However:the construction speed of sequential NPsim matrix is slower than the one of KD-tree and SR-tree.The reason is the time complexity of constructing sequential NPsim matrix is O(M2·n):but the one of constructing KD-tree and SR-tree are both O(M·log2M·n).From section 4.2.1 and 4.2.2.The operations generating different rows of sequential NPsim matrix are independent of each other:which esay be paralleled.But the parallelization for construction of index tree is hard.Therefore:the time complexity would be reduced from O(M2·n) to O(M·n) by virute of parallel.Thus:using parallel in construction of index tree is the future work.

[1] Jegou H:France L R R:Douze M:et al.Product quantization for nearest neighbor search.IEEETransactionsonPatternAnalysisandMachineIntelligence:2010:33(1):117-128

[2] Ericson K:Pallickara S.On the performance of high dimensional data clustering and classification algorithms.FutureGenerationComputerSystems:2013:29(4):1024-1034

[3] Bellman R.Dynamic Programming.Princeton:New Jersey:Dover Publications Inc:2010.152-153

[4] Andoni A:Indyk P.Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions.CommunicationsoftheACM:2008:51(1):117-122

[5] Zhang D:Wang J:Cai D:et al.Self-taught hashing for fast similarity search.In:Proceedings of the ACM SIGIR 2010:New York:ACM Press:2010.18-25

[6] Jagadish H V:Ooi B C:Tan K L:et al.iDistance:an adaptive B+-tree based indexing method for nearest neighbor search.ACMTransactionsonDatabaseSystems:2005:30(2):364-397

[7] Heisterkamp D R:Peng J.Kernel vector approximation files for relevance feedback retrieval in large image databases.MultimediaToolsandApplications:2005:26(2):175-189

[8] Yi L H.Research on Clustering Algorithm for High Dimensional Data:[Ph.D dissertation].Qinhuangdao:Institute of Information Science and Engineering:Yanshan University:2011.28-30

[9] Yang F Z:Zhu Y Y.An efficient method for similarity search on quantitative transaction data.JournalofComputerResearchandDevelopment:2004:41(2):361-368

[10] Huang S D:Chen Q M.On clustering algorithm of high dimensional data based on similarity measurement.ComputerApplicationsandSoftware:2009:26(9):102-105

[11] Shao C S:Lou W:Yan L M.Optimization of algorithm of similarity measurement in high-dimensional data.ComputerTechnologyandDevelopment:2011:21(2):1-4

[12] Wang X Y:Zhang H Y:Shen L Z:et al.Research on high dimensional clustering algorithm based on similarity measurement.ComputerTechnologyandDevelopment:2013:23(5):30-33

[13] Jia X Y.A high dimensional data clustering algorithm based on twice similarity.JournalofComputerApplications:2005:25(B12):176-177

[14] Alexander H:Charu A C:Keim D A.What is the nearest neighbor in high dimensional spaces.In:Proceedings of the VLDB 2000:Birmingham:IEEE Computer Society:2000.506-515

[15] Berkhin P.A survey of clustering data mining techniques.In:Grouping Multidimensional Data:Recent Advances in Clustering.Berlin:Springer-Verlag:2006.25-71

[16] Nielsen F:Piro P:Barlaud M.Bregman vantage point trees for efficient nearest neighbor queries.In:Proceedings of the IEEE International Conference on Multimedia and Expo 2009.Birmingham:IEEE Computer Society:2009.878-881

[17] Hetland M L.The basic principles of metric indexing.StudiesinComputationalIntelligence:2009:242:199-232

[18] Kunze M:Weske M.Metric trees for efficient similarity search in large process model repositories.LectureNotesinBusinessInformationProcessing:2011:66:535-546

[19] Navarro G.Searching in metric spaces by spatial approximation.TheVldbJournal:2002:11(1):28-46

[20] Charu C:Aggarwal:Yu P S.The IGrid index:Reversing the dimensionality curse for similarity indexing in high dimensional space.In:Proceedings of ACM SIGKDD 2000.New York:ACM Press:2000.119-129

Li Wenfa，born in 1974.He received his Ph.D.degree in Graduate University of Chinese Academy of Sciences in 2009.He also received his B.S.and M.S.degrees from PLA Information Engineering University in 1998 and 2003 respectively.His research interests include information security:data analysis and mining:etc.

10.3772/j.issn.1006-6748.2016.03.002

①Supported by the National Natural Science Foundation of China (No.61300078):the Importation and Development of High-Caliber Talents Project of Beijing Municipal Institutions (No.CIT&TCD201504039):Funding Project for Academic Human Resources Development in Beijing Union University (No.BPHR2014A03:Rk100201510) :and “New Start” Academic Research Projects of Beijing Union University (No.Hzk10201501).