网络全端可靠性仿真算法研究
2013-05-07孙慧丽陈良山
孙慧丽,陈良山
(航宇救生装备有限公司 信息管理部,湖北 襄阳 441003)
全端可靠性是指整个网络所有端点之间保持连通的概率[1],是目前主干网设计中最为流行的可靠性评价方法. 基于连通性的网络可靠性分析是网络可靠性研究中的经典问题,对任意网络的K端可靠性、全端可靠性来说,如何准确计算网络可靠性是个NP-hard问题[1-4]. 目前,针对网络K端可靠性和全段可靠性主要从两个方面来研究,其一是通过研究网络可靠性问题的数学结构,给出网络可靠性测度的绝对上下界[2-3];其二是基于随机模拟的蒙特卡罗法[4-5],它是通过对网络的部分信息进行模拟,以获取抽样信息,最后获得对网络可靠性测度的伴有置信区间的点估计. 文献[4]通过选取逐次事件估计量的方法提出了计算网络全端可靠性的三种仿真方法:蒙特卡罗仿真方法CMC (Monte Carlo Method),模块化抽样方法BS (Blocking Sampling Method)、几何抽样方法GS (Geomtretic Sampling Method). H.Cancela等提出的递归方差衰减RVR(Recursive Variance Reduction)方法,依据状态空间分解原理,把对原状态空间的抽样实验转为对其子空间的实验,在子空间的实验中递归调用本方法,直至满足终止条件.[5]笔者在文献[4]的基础上,进一步探讨了网络可靠性的三种仿真方法,并采用递归方差缩减[5]方法进行仿真实验.
计算全端可靠性满足的假设条件:
1)每条链路有两种状态:工作状态和失效状态;
2)失效链路互相独立;
3)在节点对之间不存在平行边;
4)不考虑结点失效状态,因此假设结点是完全可靠的;
5)网络是不可修复的.
本文中用到的术语:
1)G=(V,E) 是无向图,V是结点集,E是边集,|V|是结点的个数,|E|是边的个数;
2)(i,j)结点i和j之间无向连接边,即(i,j)=(j,i);
3)xij:是边(i,j)状态,若链路(i,j)工作,则xij=1;否则为0;
4)x:网络状态矢量,即x={xij:(i,j)∈E};
5)S是网络所有的状态空间,|s|是所有状态矢量的个数;
6)f(x)是网络结构函数值,如果网络在x状态下网络是连通的,则f(x)=1,否则f(x)=0;
7)pi是链路(i,j)的正常工作概率,pij=pji,如果链路(i,j)不存在,则pij=0,qij是链路(i,j)的故障概率;
1 蒙特卡罗仿真
蒙特卡罗仿真是一种简单的仿真方法,是通过对网络的部分信息进行模拟,以获取抽样信息,最后计算对网络可靠性测度的伴有置信区间的点估计值. 假设事件Yi表示第i次试验中网络G是连通的,Yi为其逆事件,用 Y ( G)表示网络G的全端可靠性,则 Y ( G)等于Y的平均值,
由于Var{Y(G)}未知,所以用它的估计量来表示,其估计量用 所示,如公式(1)所示:

蒙特卡罗仿真方法的基本思想,是先对网络G
CMC需要产生N*|E|次随机数,并进行N次网络的连通性测试. 如果一个链路(i,j)具有很高的可靠性,如当pij=0.99,事件xij=0就很少发生(相当于平均运行0.01*N次该事件才发生),这样仿真效率就会很低. 因此,CMC仿真方法代价极高. 为提高CMC的运行效率,笔者在本文中探讨两种新的仿真方法,即模块化抽样仿真和几何抽样仿真. 这两种方法仍然比较简单,但计算高可靠性链路网络具有很高的效率.
2 模块化抽样仿真
模块化抽样仿真BS是将试验次数N分成TN个大小为L的模块,且N=TN*L,假设 x( 1 ),x( 2)L x( L)是利用CMC方法生成一组大小为L的连续网络状态矢量, Zij={ xij( 1),xij( 2)L xij(L)}表示链路(i,j)的状态矢量,xij( m )表示模块中第m次试验链路(i,j)的状态;xij( m) = 0 表示第m次试验中链路(i,j)发生故障. 设Yij表示 Zij中xij等于0的个数,即每个模块中链路(i,j)发生故障的个数,则 Yij服从伯努利分布,其概率为:
模块化样本仿真方法包括以下三个步骤:1)对每条链路(i,j)利用参数为L和qij的伯努利分布函数求出样本Yij;2)随机选择Zij中Yij个个体,并把其设置为零;3)利用z构建网络的L个状态矢量空间;4)计算每个状态下f(x)的值,求出TN*L次试验中Y( G)的值.
对于小样本变量来说,与CMC相比较,BS最大的优势在于相同的试验次数下产生很少的随机数;为求出Zij,对相同的样本大小,BS需要一个伯努利随机数Yij,而CMC使用L个伯努利随机数.
3 几何抽样仿真
几何抽样仿真GS,是用几何随机变量和一个事件驱动模拟(CMC是时间驱动模拟)来产生一组状态矢量,事件驱动模拟(Event Driven Simulation)是按事件发生的先后顺序进行处理的一种模拟程序,事件表是有序表. GS的基本思想是利用上面相同的方法生成一串连续的网络状态向量 Zij={ xij( 1),xij(2)L } ,Yij表示向量 Zij= { 1,0,1,1,1,1,0,1L } 中两个0之间1的个数,即每组链路(i,j)两个故障状态之间出现工作状态的次数. 由于在参数为pij的伯努利试验中 xij( m)和 xij( k)是相互独立的,则Yij服从几何分布,所以
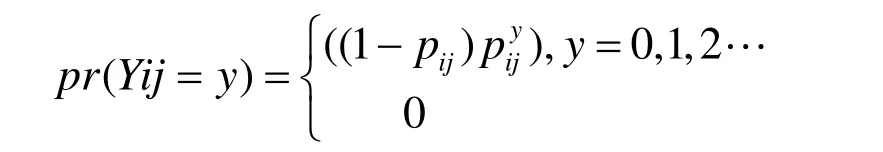
链路(i,j)的事件表表示链路(i,j)下一次出现故障时工作状态的次数,eij表示“链路(i,j)两次发生故障状态之间出现工作状态的次数”的事件,emin表示事件表中最小值,当eij等于emin时,表示链路(i,j)出现故障,对故障进行处理,处理办法为设置xij=0,更新链路(i,j)的事件表,eij=emin+Yij,否则xij=1;当emin达到终止条件时求出Yi出现的次数,从而得出网络的全端可靠性.
GS方法采用了几何分布的无记忆性特点. 根据无记忆特点可知,任意第K次和L次(K¹L)试验的协方差等于零,即Cov(,) = 0 ,则Cov(f( xk),f( xj)) = 0 . 与CMC相比,它不需要提供任何方差. 通过 模拟链路失效来产生随机数,链路(i,j)在1/qij次试验中失效1次,则几何算法需要1/qij个随机数,小于CMC所生成的随机数.
4 三种仿真方法的实现及结果比较
引论:对于相同的样本大小,如果Var(CMC))/Var(M)>1,则使用M方法计算出的值要比CMC方法精确.
Var(CMC))/Var(M)是CMC方法与M方法的样本方差比值,又称方差缩减法,以此可以判断哪种方法更精确. Var(M)和Var(CMC)分别是由方法M和CMC仿真得到的样本方差. 用表示第t次试验M仿真方法计算出的全端可靠性值,表示用M仿真方法进行K次试验的全端可靠性平均值,因此Var(M)可以用公式(2)表示.

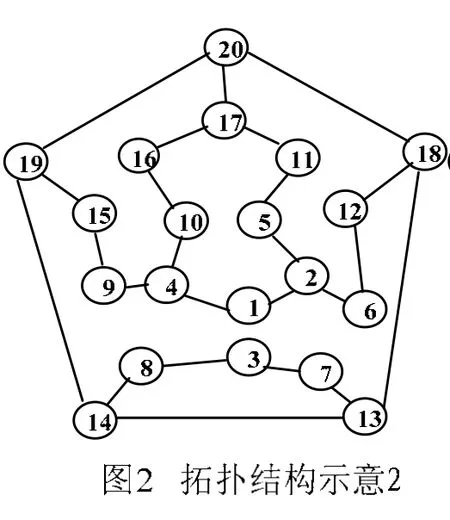
本文采用20个结点30条链路的网络拓扑结构,如图1所示. 通过对图1随机减少链路或增链路分别得到24条链路网络拓扑结构如图2所示、40条链路网络拓扑结构如图3所示.
为了简便起见,令网络节点绝对可靠,每条链路的可靠度相等,概率分别取0.90、0.95、0.99. 文献[4]中没有给出三种网络图准确全端可靠性值,本文采用因子定理准确计算三种网络图的全端可靠性值.


蒙特卡罗抽样次数为N= 5 000,抽样方法的模块大小TN=50,L=100,几何抽样的终止条件N=5 000. 程序运行K=100次,求出每次运行结果的平均值,得到全端可靠性的值,然后利用公式(2)计算三种方法的样本方差. 三种仿真算法与因子定理方法的全端可靠性仿真结果比较图以及方差缩减结果如表1、图4、图5、图6所示.

表1 三种仿真算法与因子定理方法的全端可靠性仿真结果比较图
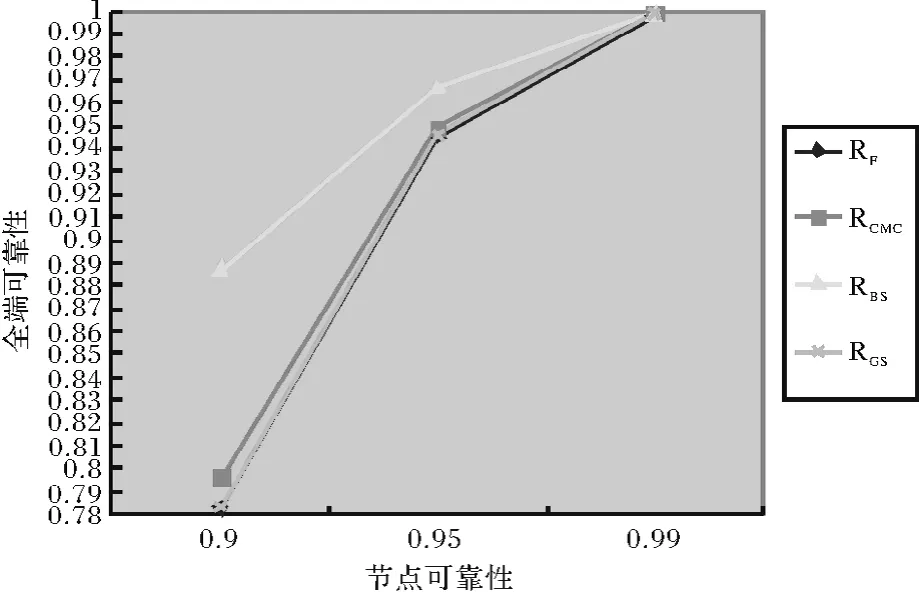
图4 图2的四种计算方法的全端可靠性比较
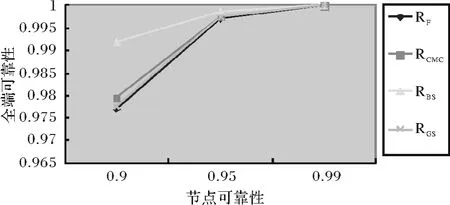
图5 图1的四种计算方法的全端可靠性比较
表1可以看出,RCMC和RGS几乎相等,相对误差为零,但在稀疏网络图2中,当链路工作的概率P小于或等于0.95时,RCMC和RGS与RF相对误差很小,RBS相对RF误差相对较大,当P大于0.95时,三种方法RCMC、RBS、RGS和RF相对误差比较小.
对于密集型的网络图1、图3,当P小于或等于0.95时,RCMC和RGS与RF相对误差较小,说明与理论值比较接近. 当P大于0.95时,RCMC、RBS和RGS相对误差比较小,因此,CMC和GS两种方法比较适用于密集型网络, BS方法适用于高可靠性链路的密集型网络.

图6 图3的四种计算方法全端可靠性的比较
对于稀疏网络,当P小于或等于0.95时,Var(CMC)/Var(BS)的比值小于1,表明BS方法仿真数据没有CMC方法准确,而其他情况,Var(CMC)/Var(BS)和Var(CMC)/Var(GS)的比值大于1,用BS方法和GS方法仿真出的全端可靠性比CMC方法精确,表明BS和GS方法的适用于密集型网络的全端可靠性的仿真.
综上所述,CMC、BS和GS优缺点如下:
CMC适用于计算稀疏网络的可靠性,算法比较简单,但是算法代价极高,运行效率比较慢.
BS适用于高可靠性密集型网络,网络中具有不同失效概率的链路;BS不需要网络结构的初始信息,易执行,不需要复杂的数据结构或数学结论.
GS适用于高可靠性链路的网络;GS占用很小的内存,并且不需要任何参数,执行起来比较简单.
BS和GS两种算法相对CMC算法而言,具有以下优点:1)较易实现,易编码;2)效率随着链路可靠性的增加而增加;3)适用于大型密集型网络,其实现取决于链路的可靠性,如果链路可靠性大于0.9时,效率就会增加.
[1] 冯海林. 网络系统中可靠性问题的研究[D]. 西安: 西安电子科技大学, 2004.
[2] 宋 月, 刘三阳, 冯海林. 节点失效下全端可靠性的上界[J]. 数学的实践与认识, 2006, 36(1): 165-169.
[3] KONAK A, SMITH A E. An Improved General Upper Bound for All-Terminal Network Reliability[[EB/OL]. (1998-10-01)[2012-10-11]. www.pitt edu/aesmith/postscript/bound.pdf.
[4] ABDULLAH KONAK. A multiobjective genetic algorithm approach to telecommunication network design problems considering reliability and performance [D]. Pennsylvania(US): University of Pittsburgh , 2001.
[5] CANCELA H, URQUHART M E. Adapting RVR simulation techniques for residual conneetedness network reliability models[J]. IEEE Transactions on Computers,2002, 51(4): 439-443.
[6] 王 芳, 侯朝桢. 一种估计网络可靠性的蒙特卡洛方法[J]. 计算机工程, 2004(30): 1813-1815.
