数学教育中的隐喻研究

谢圣英 ，喻 平

（1．南京师范大学 课程与教学研究所，江苏 南京 210097；2．长沙理工大学 数学与计算科学学院，湖南 长沙 410004）

近年来，国外学者开始越来越多地关注隐喻在数学教育中的重要作用（Pimm，1981；Presmeg，1992；Sfard，1994，2000；Núñez，Edwards & Matos，1999；Lakoff & Núñez，2000；Núñez，2000；Bazzani，2001；Robutti，2006；Edwards，2009；Özgünkoca S. Asli，2010 et al）[1~11]．“隐喻与数学教育”也是2005年欧洲数学教育研究学会第四次代表大会的讨论主题之一．但目前国内相关研究很少．为了更全面地了解并深入研究数学教育中的隐喻，研究者尝试从认知心理学基础、数学观和数学教育观3方面对其加以剖析．

1 隐喻的认知心理学基础

传统隐喻理论认为，隐喻是一种语言的修辞现象，它通过“A是B”的表达方式传递比直接表达更丰富的含义．而现代认知理论视角下，隐喻是一个深层的认知机制．Schon（1979）指出，隐喻可以被看作理解“我们如何思考、如何认识现实的意义以及看待事物的观点或方法”[12]的一种方式．美国隐喻研究专家Lakoff & Johnson（1980）认为，“隐喻植根于经验知识之中，它们（至少部分地）形成了我们做什么、以及如何理解我们正在做的事情的一种结构．”[13]

Lakoff将隐喻解读为“用一种事物来理解另一种事物”（understand one thing in terms of another）．这也是目前绝大多数研究者对隐喻的认知功能所达成的共识．此时，“隐喻”特别需要和心理学中的“迁移”加以区分．首先，隐喻具有“A是 B”的表达方式，这是它与迁移相区别的最明显标志．其次，“迁移”是指“一种学习对另一种学习的影响”[14]，它通常发生在学习过程中的两种学习之间；而隐喻中的A、B却不一定都是学习过程中的概念或事物．比如“定义域是盛着点的容器”这个隐喻（后文还会介绍），“容器”并不是数学领域中的事物或概念，它甚至和学习没有什么必然联系．“隐喻”本源上属修辞手法，因其相似，才能构成隐喻；因其不同，隐喻才有意义．另外，迁移的实质是新旧经验的整合，整合可通过3种方式实现：同化、顺化和重组[15]；而隐喻的目的是生动形象，深入浅出，把不知或难知的事物或概念等变得能知或易知，它不需将事物或概念等做任何改变．

“隐喻是从源域（source domain）到靶域（target domain）的映射，即用我们熟悉的、已知的或具体的东西去理解不熟悉的、有待理解的或抽象的东西．如果穷根溯源，人们最初熟悉的事物是什么呢？这就是我们的身体．我们的身体以及身体同世界的互动提供了我们认识世界的最原始概念．以这些身体中心的原型概念为基础，我们发展出其他一些更抽象的概念．”[16]传统的心智身体二元论认为心智可以离开身体而加以研究．具身认知心理学（embodied cognition psychology）则强调人类经验的重要性、人类身体的中心地位、人类特有的认知结构和组织的作用．具身认知的中心含义就是指身体在认知过程中发挥着关键作用，认知是通过身体的体验及其活动方式而形成的．所以，隐喻是身体、大脑、经验和心智的产物．具身认知理论为隐喻特别是身体隐喻（bodily metaphor）提供了至关重要的认知心理学理论基础．由于隐喻连接了许多身体知觉，它们对于人们建构数学实体的意义很重要．“大量非常基础，同时又非常复杂的数学思想在本质上是隐喻的．”[6]Sriraman and English（2005）在他们的数学教育研究理论框架调查中也谈到了具身认知理论的重要性[17]．

2 隐喻的数学观

2.1 隐喻的数学观是什么

探讨隐喻的数学观就是从隐喻的视角思考“数学是什么”．换言之，在“隐喻能增进数学思想的理解，促进数学教与学”的观点持有者眼中，数学的本质究竟是什么？

在隐喻的观点下，数学是一个隐喻网络．数学的隐喻网络是由基础隐喻（grounding metaphor）和连接隐喻（linking metaphor）这两种类型的隐喻联结而成的．那么，什么是基础隐喻，什么是连接隐喻呢？Lakoff & Núñez（2000）根据隐喻与数学的关系，区分了它们：基础隐喻将数学外的源域（如实物）同数学中的靶域（数学概念或意义）相联系；而连接隐喻中的源域和靶域均属于数学领域中，它只是在数学的不同分支领域间交换性质[6]．“容器”这个意象图式（image schema）可以作为理解其它更加的抽象概念（如函数的定义域）的源域．于是，构成了基础隐喻——“定义域是盛着点的容器”（见图 1）．连接隐喻如“一重积分是面积”，它则将属于数学中不同分支的微积分（积分）和平面几何（面积）联系起来．又如“数学是建筑”，意味着数学是这样一门课程：必须好好学习基础知识才能为进一步的学习提供强有力的支持．此时，“数学是建筑”这个隐喻的映射源域是“建筑必须有好的地基，才能一层一层往上盖”．当然，有的人也可以用完全不同的隐喻表达（metaphor expressions）来理解这个隐喻，如建筑上的门窗、建筑内的装饰等的隐喻意义．所以，隐喻具有单一与系统相结合的二重性（unitarysystemic duality）．一方面，隐喻的形式单一（“A是B”）；而另一方面，隐喻表达却是多样的，隐喻让人们产生一个实践系统（系统论的观点）通过源域来了解靶域（见图2）．

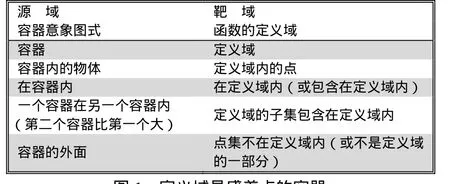
图1 定义域是盛着点的容器

Mowat & Davis（2010）关注数学概念的具身化性质以及它们对隐喻的依赖，提出了数学是隐喻网络的观点，并且利用拓扑网络理论研究了数学概念之间的联系，探讨了支撑具身化数学（embodied mathematics）的隐喻网络结构．在这个网络结构中，源域或数学中的概念域（conceptual domain）表示为网络中的结点，而基础隐喻或概念隐喻（conceptual metaphor）则在源域与概念域间或各概念域间提供联结．当靶域为数学概念时就形成了数学概念隐喻网络，可以用图3来表示数学概念隐喻网络系统的某个局部．

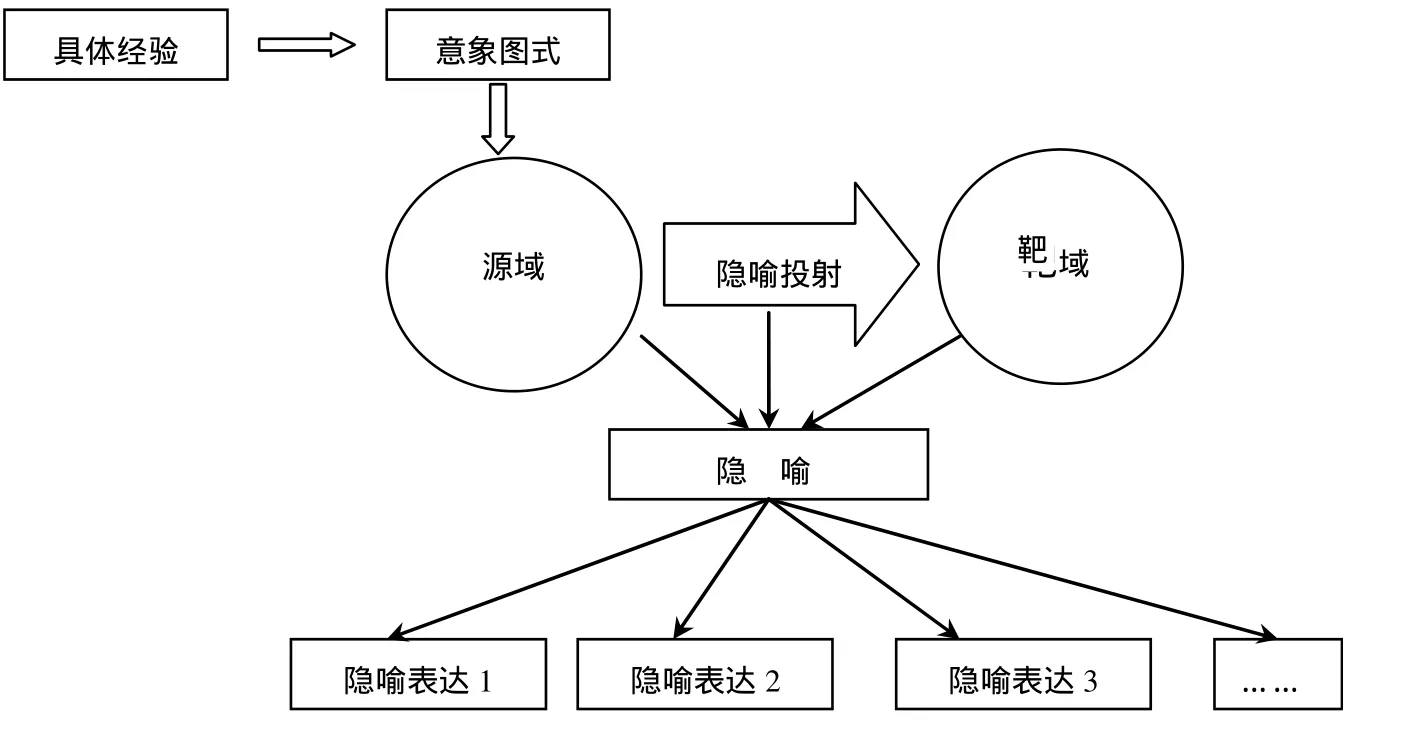
图2 描述隐喻的构成及来源（Font, Bolite & Acevedo, 2010）

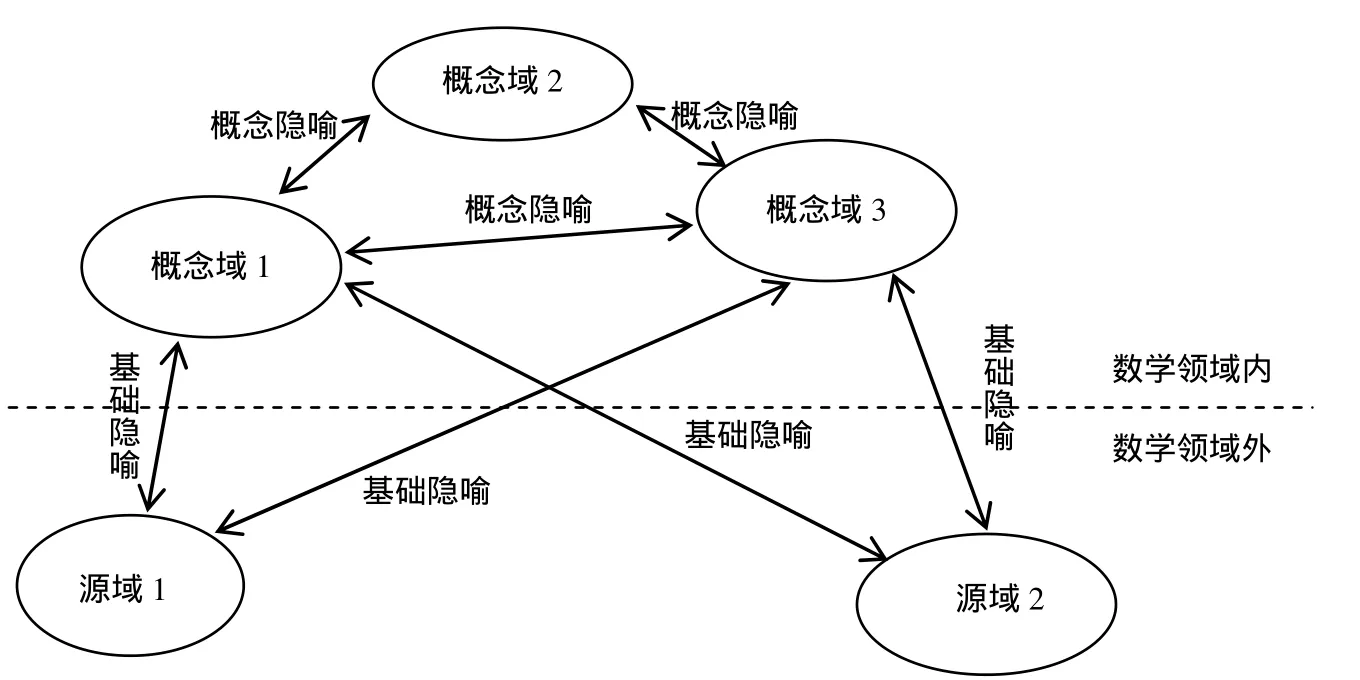
图3 数学的概念隐喻网络系统局部示意图

其实，在隐喻的观点下，数学不仅是一个隐喻网络，它还是一个复杂系统（complex system）．Mowat & Davis（2010）不仅提出了数学是隐喻网络的观点，还将数学中的这个隐喻网络同复杂系统的10条性质进行了逐一比照论证之后认为“数学是一个复杂系统”．他们对数学隐喻网络的分析提供了这种对数学知识的解释的合理性证据，研究结果发现数学的隐喻网络呈现出嵌套形式（nested forms）和无标度拓扑结构（scale-free topology），这是一个典型的复杂系统[18]．复杂系统特征是元素数目众多，而且其间存在着强烈的耦合作用．复杂系统由各种小的系统组成，例如，生态系统是由各个种群，各种生物组成的．生态系统是复杂系统的一个很好的例子．限于篇幅，在此不会对复杂系统的具体性质作详细、深入地介绍．但是，这里特别强调——数学这个复杂系统是开放和发展的．这个“复杂系统的网络”不应是“追踪（tracing）”而是“地图（map）”．“追踪”就像一棵树，它通过获得基因在枝叶中复制相同的部分来生长，而“地图”则处于不断变化的状态，图中每个部分都不完全相同．正如Deleuze & Guattari（2007）所描述：“一个‘地图’在它的所有维度上是开放和可连接的；它是可拆卸的，可逆的，容易不断修改的．”[19]也就是说，数学这个复杂系统是开放的，充满了各种连接并不断地变化发展．

总而言之，在隐喻的观点下，数学就是一个由数学的概念或意义同数学之外的实物或经验之间、数学概念或意义之间形成的复杂的隐喻网络系统．主张数学是一个复杂网络系统是很有价值的．Ernest（2010）认为将数学看成复杂系统，可以使学习者摆脱必须经历的严格的学习阶段顺序（如皮亚杰的认知发展阶段论）．在复杂系统的模式下，数学教与学同思想能够复合成为一个概念、表征、记忆等构成的互联的网络．

2.2 隐喻的数学观反思

不同时代的哲学家、数学家和数学哲学家从不同角度对“数学”的含义提出了不同的理论和观点．譬如Wittgenstein（1978）提到“斑驳混杂的数学”就承认了数学含义的多样性．数学是一个有组织的知识体、数学家从事的活动、一门学校科目、一个多义的文化体，以及一种语言和在许多不同场合使用的概念工具盒[20]．Ernest（2010）认为：“仅仅它的名字（mathematics）就不明确，因为它是用一个复数词来命名一个单独实体．”[19]隐喻的数学观从一个独特的经验论和系统论相结合的视角揭示了数学的本质和内在规律性，但它同时也不可避免地遭遇了一些质疑或否定．其中，以对身体隐喻的数学观的反思尤为突出：

首先，隐喻的数学观认为，“所有人类活动，包括做数学和学数学本质，都是人的身体运动”．譬如“化简代数方程是一种身体运动”，支撑化简代数方程的基本意义是建立在身体运动基础上的，平衡可以从两手分别向上托住秤盘力量中获得身体感受，解方程中的操作只有当他们在平衡的两端执行相同行为，即双方保持一致时才凑效．对此，Ernest（2010）提出了异议：“一致性判断不是照字面上的”[19]，数学活动应当看作是符号系统内部的记号运算．符号系统是由3个部分组成：一个符号集、一套符号的使用和生产规则、一个潜在的意义结构来结合这些符号和规则之间的关系．据此，对于一个初等代数的符号体系，平衡隐喻体现在支撑符号“=”的含义及其操作规则的意义结构（如反身性，对称性，传递性）中，而不是平衡的身体隐喻．隐喻在数学中的地位和更普遍的意义应当在潜在意义结构中被发现，而这潜在意义结构本身就是一个网络系统．

其次，由于基础隐喻（见图3）常常被形象地看成是支撑整个数学概念（意义）体系的隐喻腿（metaphor leg），而身体隐喻属于基础隐喻中的一类（它将数学外的身体体验和活动方式同数学概念或意义联系起来），所以隐喻的数学观主张身体隐喻是基本型，它可作为数学领域中其它意义形式的基础．许多学者认为这是过分绝对化、夸大了的论断．尽管Núñez（2005，2008）提供了无限逼近、超穷基数、连续函数等的一些高等数学概念中使用隐喻的例子[21~22]，Mason（2010）还是指出“很多数学中的概念包含了隐喻（传递意义），但它也有心理和逻辑等其它成分在其中起作用”[23]．仅仅建立在简单地观察集合和函数的作用而得到的论断不管用，对于更加复杂的数学结构，比如科赫雪花曲线、希尔伯特填充曲线（它们的尺寸是正实数而不是整数，而且巧妙地运用了超穷基数），通常不那么容易找到它们直接的具身基础．McGowena & Tall（2010）也认为，虽然隐喻的一般概念可能为数学思想提供深入的分析，但更重要的是要考虑到个人的“前见”（met-before）．“前见”将经验建构的个体特殊心理结构提供给个体，可是“前见”并不一定直接建立在身体隐喻之上[24]．“不是所有隐喻都能被肢体动作捕获，同样，也不是所有的肢体动作都通过隐喻来发挥符号功能．将肢体动作作为所有数学概念的隐喻基础，是将潜在洞察力延伸得太远”[19]．事实上，身体隐喻仅是皮尔斯的符号三元组合分析（icon，index and symbol）中的一元（相似表象）的一部分．皮尔斯的相似模式包含了各种形式的隐喻和类比，大大超出了Lakoff & Núñez（2000）强调将身体隐喻作为数学的基础．

此外，有研究者对隐喻为更成熟概念提供基础的观点提出了批评，认为隐喻不够精确、不够可靠，依赖隐喻是心灵偷懒的表现．如“Bachelard Gaston将常识性心灵对直观形象的依赖看作是滋生认识论障碍的温床……[这些]往往没有明确制定约束条件，而只是在潜隐的假设、认知或知觉习惯层次进行操作”[19]．同时还有研究指出，隐喻派生的不成熟的观念，有可能会导致对数学概念的错误理解．如郜舒竹等（2011）发现数学术语中，通常是用词语的一般日常意义隐喻其数学意义，这种隐喻存在着指称对象模糊或变异等隐喻歧义的现象[25]．

3 隐喻的数学教育观

迄今为止，关于什么是数学教育观，一直没有一个统一的说法[26]．但是，研究数学教育中的隐喻又确有必要将隐喻的数学教育观予以澄澈．不妨从隐喻观点下的教育目的、教育方法入手，对隐喻的数学教育观进行一番检视．

3.1 隐喻的数学教育目的观

在隐喻观点下，数学教育的目的就是要改变数学封闭、冰冷的面貌，培养和激发学生的数学想象力和数学直觉．让每一位学生都学会通过熟悉的事物、相似的情境和已有的经验来学习和亲近数学，学会用普遍联系的观点、态度和方法观察和处理现实世界中的数量关系和空间形式的有关问题；让教师可以透过隐喻深入剖析学生个人的一些数学错误和困难的认识根源，甚至体会学生的数学情感、态度和价值观，反思和改进自己的教学．

一方面，不仅教师可凭借隐喻实现深入了解和指导学生的个体知识（或称缄默知识、默会知识）的愿望，隐喻还能帮助数学教育工作者之间、师生之间交流和反思课堂上产生的集体知识和课本中的公共知识．因为隐喻网络的无标度拓扑结构能清楚地显示学生学数学和用数学的困难原因，而且保证数学概念同许多源域有隐喻连接，还能促进学生对数学的理解．总之，无论是作为个人理解的数学，还是作为一个正式的学习领域的数学，分析它们的隐喻网络结构都可以为人们提供一些新的见解或启示．

另一方面，让教师或学生用隐喻描述他们对数学的看法和观点，并让他们解释自己的隐喻，这为研究者和教师观察和研究学生的情感领域，教师或学生停下来反思和调试自己的情感、态度和价值观提供了很独特的机会．有研究者（Noyes，2006；Reeder，Utley & Cassel，2009）运用隐喻理论探索了职前数学教师的数学观和教学观[27~28]．杨光伟等（2006）将小学生构建“数学是什么”的隐喻分类，归纳了学生的3种主要数学观念，并发现学生使用的隐喻与他们提出的数学学习建议之间存在一定关联[29]．Özgün-Koca（2010）使用隐喻研究比较了初中生、高中生和大学生的数学情感和态度以及产生该情感倾向的原因[11]．此类研究比较多，类似的还有Schinck等（2008）的研究[30]．

3.2 隐喻的数学教育方法

首先，教师不要一下子引入太多的隐喻，因为这样有可能使学生对它们产生混淆．但是，一门课程或者一个单元的教学里，教师应当保证使用一定量的各种隐喻．这些“隐喻要精挑细选，学生要很熟悉隐喻的源域，而且隐喻要精确地反映靶域结构的某些方面”[31]．如果运用成功，概念隐喻甚至可以达到无意识和自动化的程度．但在此之前，学生必须对此有足够的经验．教师可以提供活动、形象、模型和解释来促成隐喻的使用和理解．如学习负数的运算时，课堂和课本上经常使用的概念隐喻——“计算是沿着一条路径运动”以数轴和温度计作为隐喻的源域．甚至有研究认为学生理解数学模型、数学文字题就有隐喻式思维的参与[32~33]．

另外，运用隐喻需要特别地努力整合不同的推理结构，使之成为一个有机的整体．不同的隐喻有自己不同的推理结构和隐喻表达，它会“导致学生产生有意识或无意识的各种信念，从而阻碍他们将靶域的不同方面整合成一个核心概念”[34]．Núñez，Edwards and Matos（1999）研究学生在学习函数的连续性产生困难的原因，发现其中使用了两种互相冲突的隐喻；尽管这两种隐喻反映的是相似，甚至相同的数学术语，但是这些联结拥有完全不同的具身基础[5]，由于学生们很少被告知这种区别，从而导致了该学习困难的产生．

最重要的是，要帮助数学教师理解隐喻在数学教育中的作用并辅助他们发展教学技能；此外，还需要帮助教师增加连接数学概念和意义的各种各样的隐喻．做到这点并不容易，因为目前数学隐喻的研究还不够广泛，而且隐喻的识别需要教师对语言、动作、形象、比较和应用等保持敏感地关注．为了更好地运用隐喻来理解数学，数学教师需要提取这些细微的迹象，识别隐藏的隐喻，并和学生一起分享它们．有研究者观察高中数学教师在教函数的图像表征时的课堂语言和动作，发现存在4种不同的隐喻类型，但是教师们并没有意识到自己使用了隐喻[35]．Abrahamson，Gutiérrez &Baddorf（2012）研究分析了就某个数学问题一对一访谈学生时产生的3个隐喻：蛇形、波涛和涟漪、机器人，发现隐喻具有独特性、即兴性和松散性．在学生探究数学的过程中努力地类比时，教师要敏感地及时引导[36]．

3.3 隐喻的数学教育观反思

从前文的分析中不难发现，隐喻的数学教育观应当可以认为属于社会建构主义的数学教育观．虽然社会建构主义的数学教育观把数学学习或意义的获得看成是个体自我建构的过程，但它更关注社会性的客观知识在个体主观知识建构中的中介作用，更重视社会的微观和宏观背景与自我的内部建构之间的相互作用，并视它们为不可分离、循环发生、彼此促进、统一的社会过程．“社会建构主义其实并不是什么‘主义’而是一种对知识的新的研究方式……社会建构主义主要研究知识的生产过程．”[37]隐喻的数学教育观正是这样一种社会建构主义的教育观，它提醒人们要在数学知识的生产和社会建构的过程中理解数学教育．隐喻恰好可以是社会性客观知识与个体主观知识之间联结的纽带．以隐喻为中介的数学教育可以为客观知识和主观知识之间、主观知识与主观知识之间提供互动和交流的舞台．

需要特别强调的是，隐喻的数学教育观和数学观是紧密联系在一起的．在隐喻的观点下，产生的对数学本质的经验论和系统论相结合的认识，以及对数学隐喻网络系统的开放和发展的理解；这些都直接决定了关注数学知识的社会构建、打破封闭的数学“硬壳”的教育目的的确立；也直接影响了建立数学与个人体验及生活情境的广泛联系、注重数学交流和分享的教育方法的选择．诚然，除了数学观之外，还有许多因素制约着隐喻的数学教育观，例如广泛而普遍的社会文化心理、主流社会价值取向以及传统教育思想等，都会对数学教育价值观产生一定影响，但不能否认隐喻的数学观同隐喻的数学教育观的形成与发展有十分重要的关联．

应当承认，隐喻可以被比作一把双刃剑．特别是隐喻这种独特的、想象的结构可能在教学对话中被滥用，因为它比传统的教学需要给予更多的专注、个性化的脚手架和时间的投入．此外，对于隐喻在数学教育中的实际作用，特别是，究竟“先隐喻后理解”还是“先理解后隐喻”还存有疑虑．“学习者不一定能将不同的表象模式整合为一个唯一的核心概念．从使用建构好的具体材料和教具的经验中生成出抽象概念，这是一个数学教育中的老生常谈，与其说它是一个已证明的发现倒不如说是一种信仰．”[19]已有研究也表明学习者总是无法将同一个概念的不同表征联系起来，如Hart（1989）研究发现，虽然学者们可能会看到隐喻连接不同的活动，孩子们却常将隐喻连接的两个活动看作无关的、具有独立的意义和程序规则的活动[38]．“这有可能是不强调不同表征间的联系和共同结构的糟糕的教学计划所导致的后果，但这也可能归咎于一个更为深层的问题，即为学习者提供两种人们认为拥有共同结构的表征，并期待学习者发现这两个表征之间的联系，特别是当其中一个表征更抽象而另一个表征更具体，这可能犯了期待学习者提前去使用他们仍在建构过程中的抽象概念的错误．也许直到这个概念已经在脑海中形成，人们才能看到作为一个抽象概念的隐喻的具体情形．如果是这样，那么在数学教育中使用隐喻的建构素材就存在严重的缺陷．”[19]Ernest（2010）的这一评论可谓切中要害，这也同时解决了进一步研究数学教育中隐喻的可能性和必要性．

隐喻由原本属于语言学领域的一种修辞现象进入认知心理学领域，它与具身认知理论的联系十分密切，并且在数学教育领域中获得了越来越多的关注和应用．通过剖析隐喻的数学观和数学教育观，可以较为本质地理解隐喻在数学教育中的地位和作用，发现隐喻作为一种数学教学和数学教育研究的工具，能发挥其它方法所不可替代的独特功能和辅助作用．隐喻似一缕温暖和煦的春风，它给注重精确、逻辑、抽象和理性的严冬带来了想象、创造、体验和热情的活力．毋庸置疑，这为当前的中国数学教育改革也提供了重要的启示和借鉴．

[1] Pimm D. Metaphor and Analogy in Mathematics [J]. For the Learning of Mathematics, 1981, 1(3): 47–50.

[2] Presmeg N C. Prototypes, Metaphors, Metonymies, and Imaginative Rationality in High School Mathematics [J].Educational Studies in Mathematics, 1992, 23(6): 595–610.

[3] Sfard A. Reification as the Birth of Metaphor [J]. For the Learning of Mathematics, 1994, 14(1): 44–54.

[4] Sfard A. Steering (dis) Course between Metaphors and Rigor: Using focal Analysis to Investigate an Emergence of Mathematical Objects [J]. Journal for Research in Mathematics Education, 2000, 31(3): 296–327.

[5] Núñez R, Edwards L, Matos J F. Embodied Cognition as Grounding for Situatedness and Context in Mathematics Education [J]. Educational Studies in Mathematics, 1999, 39(1–3): 45–65.

[6] Lakoff G, Núñez R. Where Mathematics Comes from [M]. New York, NY: Basic Books, 2000.

[7] Núñez R. Mathematical Idea Analysis: What Embodied Cognitive Science Can Say about the Human Nature of Mathematics [A]? In: Nakaora T, Koyama M. Proceedings of PME 24 [C]. Hiroshima: Hiroshima University, 2000.

[8] Bazzani L. From Grounding Metaphors to Technological Devices: a Call for Legitimacy in School Mathematics [J].Educational Studies in Mathematics, 2001, 47(3): 259–271.

[9] Robutti O. Motion, Technology, Gesture in Interpreting Graphs [J]. International Journal of Computer Algebra in Mathematics Education, 2006, (13): 117–126.

[10] Edwards L. Gestures and Conceptual Integration in Mathematical Talk [J]. Educational Studies in Mathematics, 2009,70(2): 127–141.

[11] Özgün-koca S Asli. If Mathematics Were a Color [J]. Ohio Journal of School Mathematics, 2010, 62(4): 5-10.

[12] Schon D. Generative Metaphor: A Perspective on Problem Solving in Social Policy [A]. In: Ortony A. Metaphor and Thought [C]. New York: Cambridge University Press, 1979.

[13] Lakoff G, Johnson M. Metaphors We Live By [M]. Chicago: the University of Chicago Press, 1980.

[14] 施良方．学习论—学习心理学的理论与原理[M]．北京：人民教育出版社，1994．

[15] 姚梅林．学习迁移研究的新进展[J]．北京师范大学学报（社会科学版），1994，（5）：99-104．

[16] 叶浩生．具身认知：认知心理学的新取向[J]．心理科学进展，2010，（18）：705–710．

[17] Sriraman B, English L D. Theories of Mathematics Education: a Global Survey of Theoretical Frameworks/Trends in Mathematics Education Research [J]. ZDM, 2005, 37(6):450–456.

[18] Mowat E, Davis B. Interpreting Embodied Mathematics Using Network Theory: Implications for Mathematics Education [J]. Complicity: an International Journal of Complexity and Education, 2010, 7(1): 1-31.

[19] Ernest P. Mathematics and Metaphor: a Response to Elizabeth Mowat & Brent Davis [J]. Complicity: an International Journal of Complexity and Education, 2010, 7(1): 98-104.

[20] Wittgenstein L. Remarks on the Foundations of Mathematics [M]. Cambridge: MIT Press, 1978.

[21] Núñez R. Creating Mathematical Infinities: Metaphor, Blending, and the Beauty of Transfinite Cardinals [J]. Journal of Pragmatics, 2005, (37): 1 717-1 741.

[22] Núñez R. A Fresh Look at the Foundations of Mathematics: Gesture and the Psychological Reality of Conceptual Metaphor [A]. In: Cienki A, Müller C. Gesture and Metaphor [C]. Amsterdam: John Benjamins, 2008.

[23] Mason J. Your Metaphor or My Metonymy? A Response to Elizabeth Mowat & Brent Davis [J]. Complicity: An International Journal of Complexity and Education, 2010, 7(1): 32-38.

[24] McGowena M A, Tall D O. Metaphor or Met-Before? The Effects of Previous Experience on Practice and Theory of Learning Mathematics [J]. Journal of Mathematical Behavior, 2010, (29): 169-179.

[25] 郜舒竹，张平仁，王智秋．数学术语的隐喻歧义及其人文内涵[J]．课程·教材·教法，2011，31（2）：51-57．

[26] 曹一鸣，黄秦安．中国数学教育哲学研究30年[M]．北京：科学出版社，2011．

[27] Noyes A. Using Metaphor in Mathematics Teacher Preparation [J]. Teaching and Teacher Education, 2006, (22):898-909.

[28] Reeder S, Utley J, Cassel D. Using Metaphors as a Tool for Examining Preservice Elementary Teachers’ Beliefs about Mathematics Teaching and Learning [J]. School Science & Mathematics, 2009, 109(5): 290-297.

[29] 杨光伟，张波．小学生数学隐喻的研究[J]．数学教育学报，2006，15（3）：60-63．

[30] Schinck A G, Neale Jr H W, Pugalee D K, et al. Using Metaphors to Unpack Student Beliefs about Mathematics [J].School Science & Mathematics, 2008, 108(7): 326-333.

[31] Chiu M M. Using Metaphors to Understand and Solve Arithmetic Problems: Novices and Experts Working with Negative Numbers [J]. Mathematical Thinking and Learning, 2001, 3(2/3): 93-124.

[32] Carreira S. Where There’s a Model, There’s a Metaphor: Metaphorical Thinking in Students’ Understanding of a Mathematical Model [J]. Mathematical Thinking and Learning, 2001, 3(4): 261-187.

[33] Danesi M. A Conceptual Metaphor Framework for the Teaching of Mathematics [J]. Studies in Philosophy and Education, 2007, (26): 225-236.

[34] Watson A, Spyrou P, Tall D. The Relationship between Physical Embodiment and Mathematical Symbolism: the Concept of Vector [J]. The Mediterranean Journal of Mathematics Education, 2003, 1(2): 73-97.

[35] Font V, Bolite J, Acevedo J. Metaphors in Mathematics Classrooms: Analyzing the Dynamic Process of Teaching and Learning of Graph Functions [J]. Educational Studies in Mathematics, 2010, 75(2): 131–152.

[36] Abrahamson D, Gutiérrez J F, Baddorf A K. Try to See It My Way: the Discursive Function of Idiosyncratic Mathematical Metaphor [J]. Mathematical Thinking and Learning, 2012, 14(1): 55-80.

[37] 安维复．社会建构主义：后现代知识论的终结[J]．哲学研究，2005，（9）：60-67．

[38] Hart K A. There Is Little Connection [A]. In: Ernest P. Mathematics Teaching: the State of the Art [C]. London, Falmer Press, 1989.