改进型过零点测频法在常规弹药转速提取中的应用*
2013-04-30张晓明尚剑宇龙达峰黄建林
张晓明 ,尚剑宇,龙达峰,黄建林,刘 俊,2
(1.中北大学电子测试技术重点实验室,太原030051;2.中北大学仪器科学与动态测试教育部重点实验室,太原030051)
目前,国内外对于弹体转速的测试虽属成熟阶段,但仍不能满足高旋弹转速测量的要求[1]。传统的微惯性器件量程小,不适用于高速旋转的常规炮弹;磁阻传感器通过测量当地地磁场矢量信息,可实现对高旋弹丸的转速测量[2-3],且其成本较低、抗过载能力强、量程大[4-6]。
磁阻传感器用于转速测量时,将其沿弹丸径向安装,其输出信号与转速同频率,对该信号进行时频分析即可得到弹丸转速。
常用的时频分析方法有时域和频域分析方法。时域分析方法实时性较好,但易受噪声干扰;频域分析方法抗噪能力强,但实时性较差,且存在测不准原理[7],即不能保证时间分辨率和频率分辨率同时都很高。本文研究的常规弹转速变化相对缓慢,要求频率分辨率足够高才能正确反映弹丸的转速信息。若采用频域分析方法,提高频率分辨率会导致时间分辨率降低,因此选用时域分析方法。
常用的时域分析方法有“峰值检测法”和“过零点检测法”。当信号采样频率较低或者信噪比较小时,“峰值检测法”得到的峰值点有时并不是真实峰值,该方法精度较低;“过零点检测法”精度较“峰值检测法”高,但也存在易受噪声、零点偏置和采样频率影响的问题。综合考虑后,过零点测频法较适用于弹丸转速的实时提取。
一般而言,对于具有较高信噪比的信号,可以采用基于“线性插值”的传统过零点测频法提取其频率,但当信号信噪比较低时,真实的零点附近会出现多个由于噪声产生的干扰零点。此时,传统的过零点测频法难以确定零点的准确位置。
针对以上问题,提出了基于“最小二乘法[8-10]”的改进型过零点测频法。此方法抗噪性能强,精度较传统过零点测频法显著提高。本文以磁测信号为研究对象,分别采用传统的“线性插值”过零点测频法和基于“最小二乘法”的改进型过零点测频法分别提取该信号的频率并做误差分析,比较得出误差较小的过零点测频方法,并对该方法的一些特性进行分析;最后采用该误差较小的过零点测频方法提取某实弹测试数据的转速信息,验证该方法的可行性。
1 磁阻传感器输出信号频率提取方法
转速的测试信号源于捷联在弹体上的磁阻传感器敏感到的当地地磁场矢量信息,该信号和转速同频率。采用过零点测频法提取该信号的频率即可得到弹丸转速。
过零点测频法主要通过检测信号的过零点,计算它们之间的时间差来估计频率。每分析半个周期的信号,会得到两个过零点,进而得到一个频率点,采样率较低;此外,由于磁阻传感器输出信号频率缓慢变化,将导致得到的t-f数据采样不均匀,实际应用过程中需进行插值。由于实测曲线数字化后得到的信号由一个个的离散点连线而成,测试点不一定正好是零值点,而在y=0处所对应的x值附近几点组成的曲线很接近直线[11],故可通过拟合零点附近点来求出过零点。
传统的零点拟合法[12]为“线性插值法”,即求相邻两点之间的平均角速度,是一种粗略的求法,其缺点是当信号中存在噪声时,会影响零点位置的正确判断;基于“最小二乘法”的过零点测频法,由于在拟合零点时引入了更多的点,抗噪性能增强。
1.1 线性插值法
线性插值法拟合过零点原理:设一段曲线中某过零点的前一点和后一点位置坐标为(x1,y1)、(x2,y2),设此过零点坐标为(x0,y0),其中 y0=0。
根据两点式求直线方程
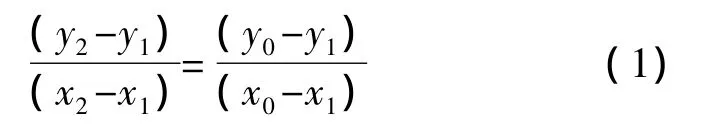
当 y0=0 时,则原理示意图如图1所示。
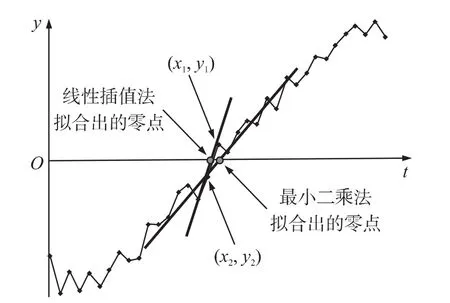
图1 两种零点拟合方法原理示意图
1.2 最小二乘法
设一段曲线中零点前n点的位置坐标为(x1,y1)、(x2,y2)…(xn,yn),后 n 点的位置坐标为(x11,y11),(x22,y22)…(xnn,ynn)。
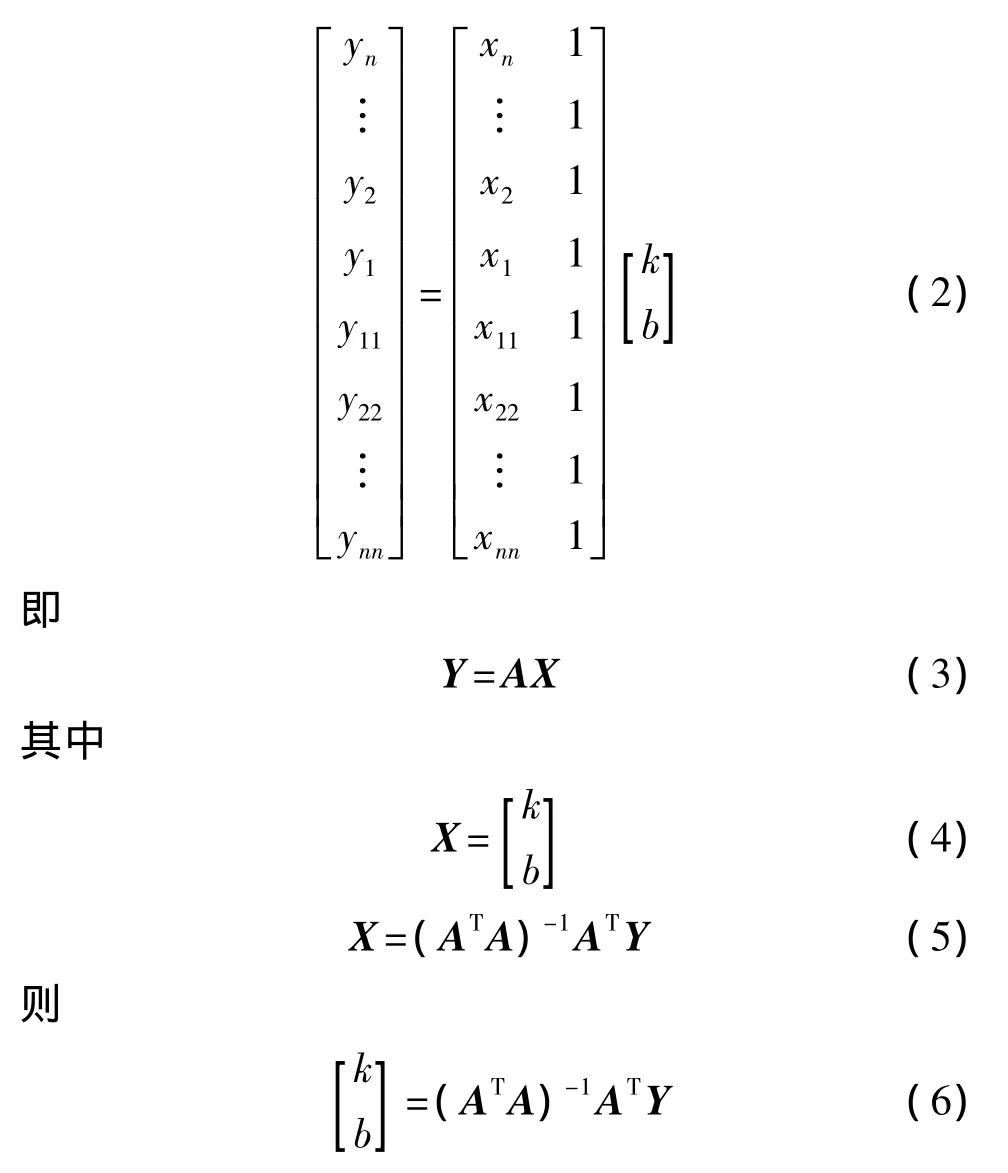
由此解出k、b,进而得到零点位置x0。原理示意图如图1所示。
研究表明,当被拟合曲线接近直线时,n值越大,算法受零均值噪声影响越小;当被拟合的曲线非线性较强时(例如正弦曲线),仅可将零点附近小范围内的曲线近似为直线。此时,若n值选取较大,会引入误差;n值选取较小,算法抗噪性能降低。
其实,n值与分析区间中所包含的信号长度占整周期信号长度的比例(即“相位角”)成正比。当信号采样频率固定后,相位角θ反映的即是n值。
2 算法特性MATLAB仿真分析
2.1 理论弹丸转速
为了对两种过零点测频算法进行评估,需要理论转速作为参考标准。利用柔格里半经验公式[13]可获得旋转弹自转角速度衰减规律,即理论转速。
由柔格里半经验公式得弹丸自转角速度ω:
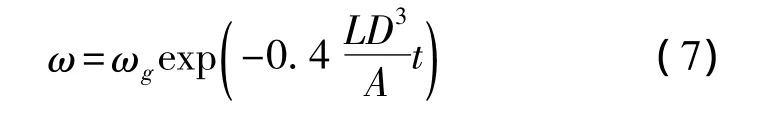
式中:ωg为弹丸膛口自转角速度,L为弹丸全长,D为弹径,A为弹丸极转动惯量。对式(7)积分即可得到弹丸滚转角γ计算公式:
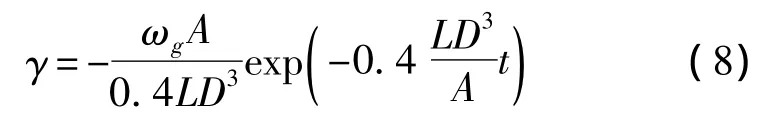
2.2 仿真初始条件
本文以某常规炮弹为例,仿真一条单轴磁阻传感器信号,传感器敏感轴沿弹丸径向安装。仿真过程中用到的初始参数如下:
射角θ0=50°;膛口自转角速度ωg=50 r/s;目标距水平面垂直距离L0=400 m;初速v0=594 m/s。信号的采样频率为1 000 Hz,信噪比为21.60 dB。
当以45°射向发射弹丸后,弹丸飞行时间持续66.7 s,磁阻传感器的输出信号如图2所示。该信号为类正弦曲线,周期缓慢变化。
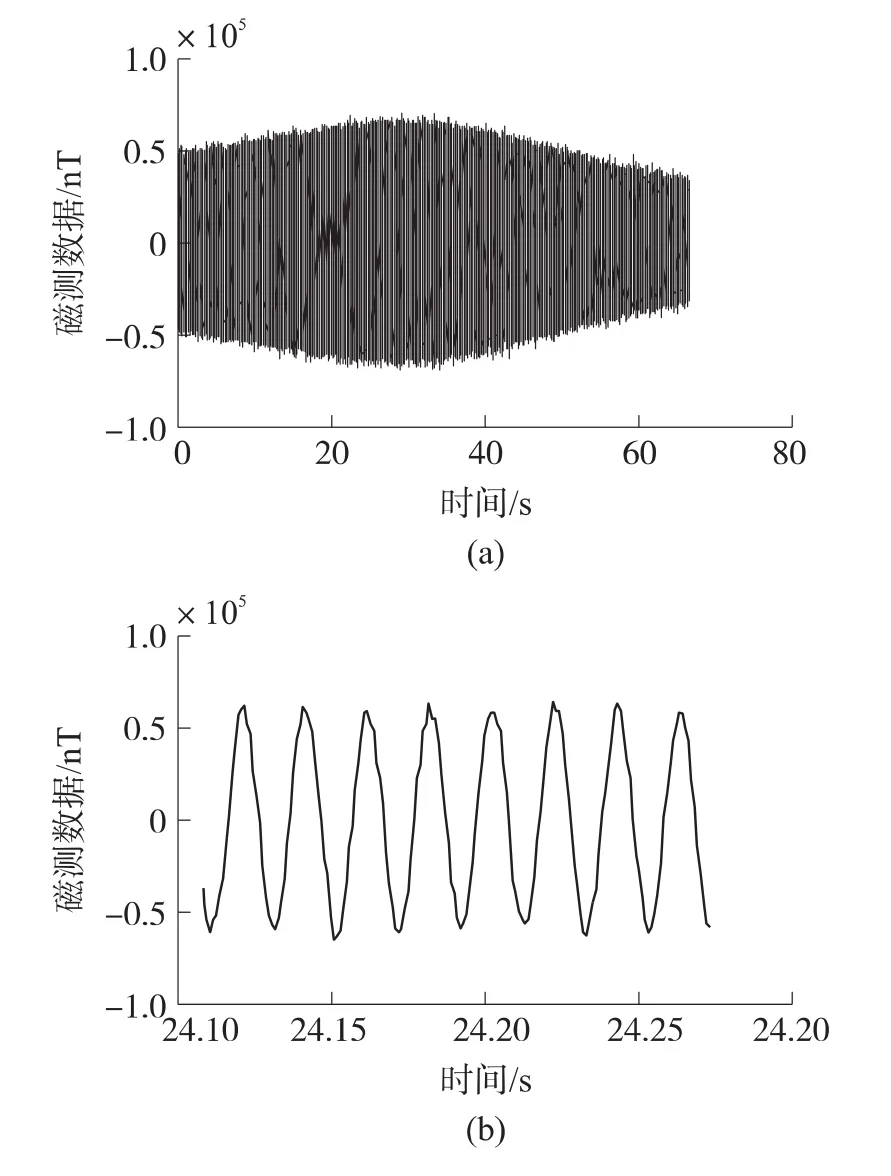
图2 磁测数据及其展开图
图3是采用柔格里半经验公式求解出的弹丸理论转速,从初始的50 r/s缓慢衰减到48.4 r/s。
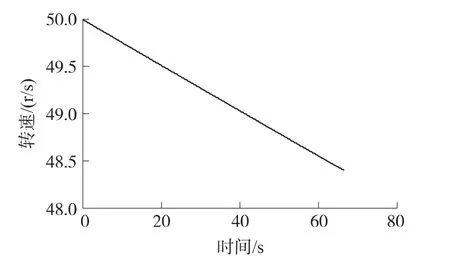
图3 弹丸理论转速
2.3 两种过零点测频方法误差对比
图4为通过“线性插值”过零点测频法求解出的弹丸转速同理论转速做误差分析后得到的转速绝对误差曲线,其转速绝对误差标准差为14.44°/s。
图5为通过“最小二乘”过零点测频法求解出的弹丸转速同理论转速做误差分析后得到的转速绝对误差曲线,其转速绝对误差标准差为7.45°/s,比“线性插值”过零点测频法误差小。

图4 弹丸转速绝对误差曲线
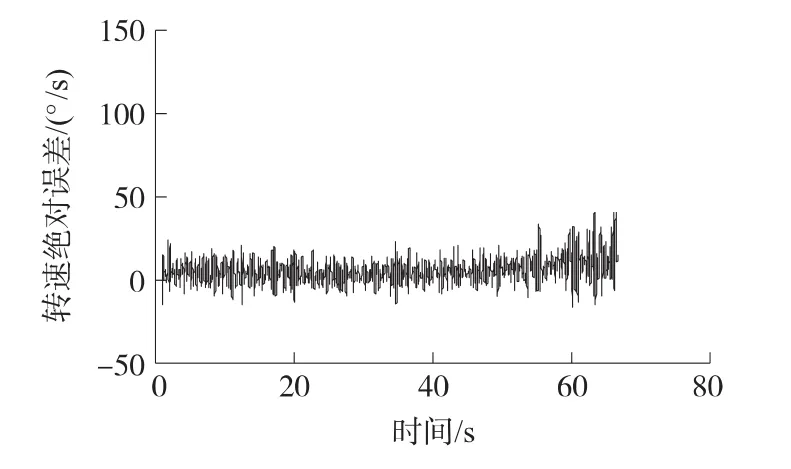
图5 弹丸转速绝对误差曲线
2.4 SNR对两种过零点测频方法误差的影响
通过2.3节的仿真分析,在以上初始条件下,“最小二乘”过零点测频法用于提取弹丸转速时误差较小。研究表明,信噪比(SNR)对过零点测频法的误差有直接影响。以下将分析SNR对两种算法误差的影响。
图6为当信号采样频率为1 000 Hz、信噪比变化范围是17 dB~57 dB时,两种测频方法精度受SNR影响的对比图。可见,两种测频方法的误差随着SNR的增加都在减小,小到一定程度后,变化不再明显;但在此过程中,“最小二乘”过零点测频法的误差较“线性插值”过零点测频法小。以下分析导致此情况的原因,仿真结果如图7所示。
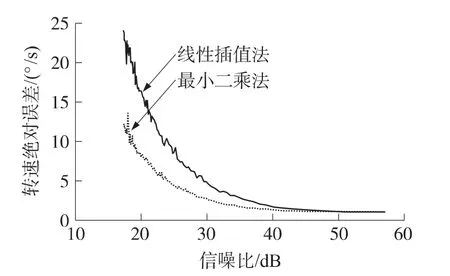
图6 SNR对弹丸转速提取误差的影响
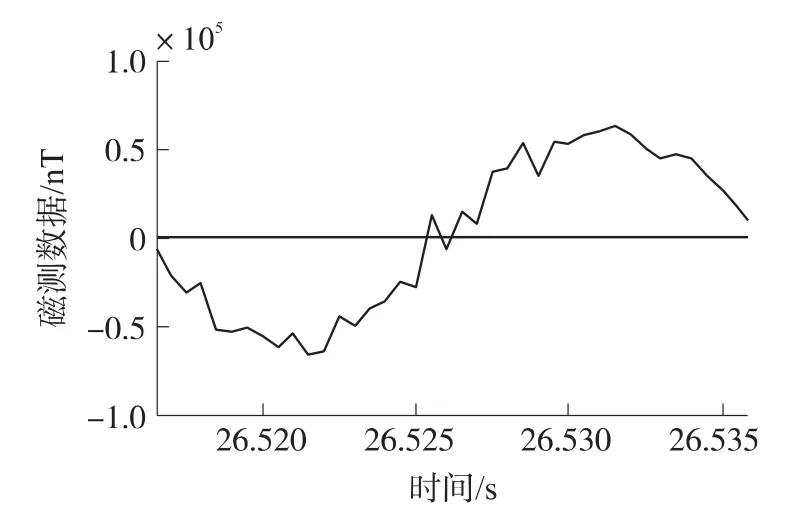
图7 SNR为23 dB时磁传感器信号
当信号SNR较小时,由于噪声能量较大,有用信号中本应该只有一个过零点的位置附近出现较多的“伪零点”(如图7所示),此时采用线性插值法难以确定零点的准确位置;最小二乘法由于引入了更多的点来拟合零点位置,可以解决以上的问题。因此,最小二乘法用于拟合零点时误差比线性插值法小。
实际应用过程中,针对SNR较高的信号,两种方法皆可用来提取转速,若对实时性要求较高,建议采用“线性插值”过零点测频法;对于被噪声污染较为严重的信号,最好采用“最小二乘”过零点测频法。
2.5 相位角对“最小二乘”过零点测频法精度的影响
相位角会影响最小二乘法拟合零点的精度,以下研究使“最小二乘”过零点测频法误差达到最小的最佳相位角选取原则。
令信号采样频率为5 kHz,SNR变化范围是12 dB~57 dB,使“最小二乘”过零点测频法误差达到最小的相位角随SNR变化的曲线及其拟合曲线如图8所示。由图8可知,采用“最小二乘”过零点测频法提取某一信号的频率时,最佳相位角受SNR影响较大。随着SNR的增大,最佳相位角在减小。分析图8中的拟合结果,可得相位角选取普遍规律,即针对SNR低的信号,应适当增大相位角;针对SNR高的信号,应通过减小相位角来提高实时性。
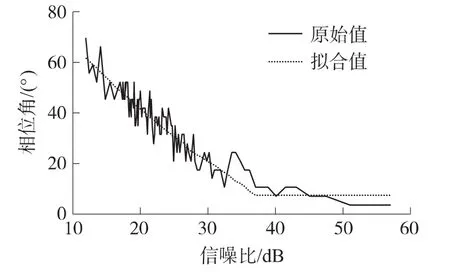
图8 最佳“相位角”受SNR影响曲线
3 实弹数据分析
为验证“最小二乘”过零点测频法提取磁传感器信号转速的有效性,以下给出1组采用实验室自制滚转角磁测系统测试某型号常规弹转速的实弹试验数据。该滚转角磁测系统采用三轴磁阻传感器HMC1043,量程为±6 Gauss,分辨率为 1.0 mV/(V·gauss-1)。图9为本次实弹实验中磁阻传感器信号波形图,其周期总体趋势先是增大而后逐渐减小,反映的运动规律是该常规炮弹转速先增大后减小。
图10是实际测试的数据经过“线性插值”过零点测频法和“最小二乘”过零点测频法计算得到的炮弹转速曲线。两者的转速绝对误差标准差为38.5°/s。可见,两种测频方法皆实现了弹丸转速的提取,但基于“最小二乘”的改进型过零点测频法误差较小,抗噪性能强。
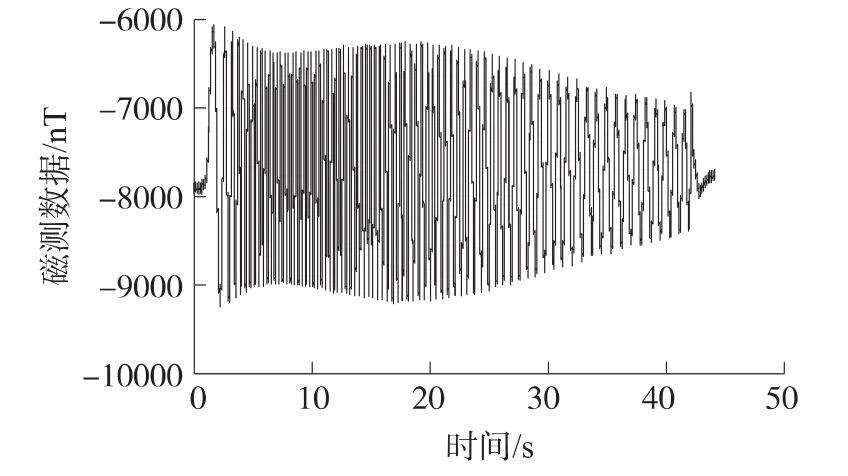
图9 磁阻传感器实测数据
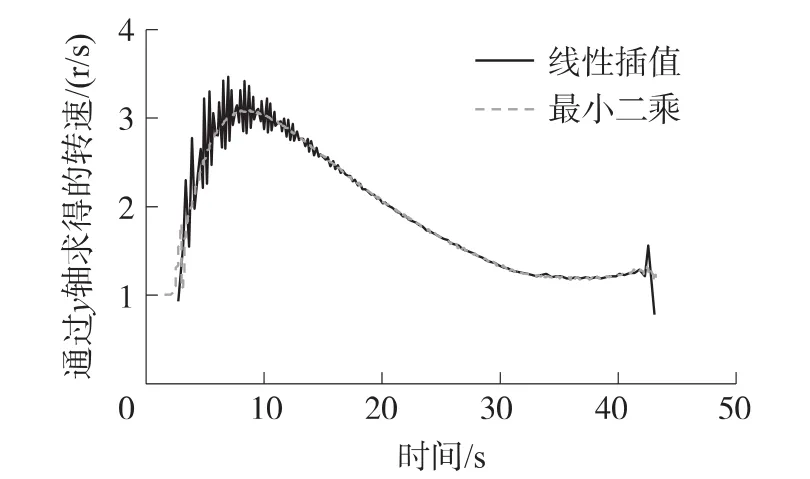
图10 某型常规炮弹转速图
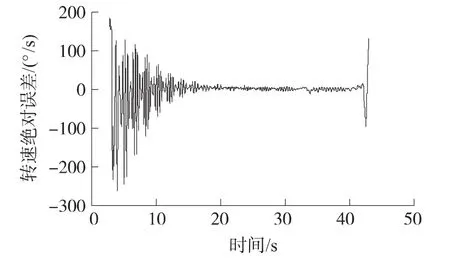
图11 炮弹转速绝对误差曲线
4 结论
(1)“最小二乘”过零点测频法较传统方法解算误差小、抗噪性能强;
(2)“最小二乘”过零点测频法精度受SNR影响较大,因此分析信号前应进行预处理:去噪、去零点偏置;
(3)“最小二乘”过零点测频法精度受“相位角”选取的影响。分析特定信号时,可参考图8中得出的最佳相位角选取原则。
(4)采用“最小二乘”过零点测频法提取常规弹转速时得到的t-f采样不均匀,需进行相应的均匀插值。
[1]张慧,曹咏弘,马铁华,等.基于线圈式地磁传感器的高速旋转弹转速测试[J].战术导弹技术,2009(4):64-67.
[2]娄朝飞,张锐.地磁传感器在自旋导弹惯测组合中的应用研究[J].航天控制,2008,26(2):41-46.
[3]愈卫博,高敏.基于传感器零值输出的旋转弹丸磁航向测量方法[J].探测与控制学报,2009,31(1):19-22.
[4]王广龙,祖静,张文栋,等.地磁场传感器及其在飞行体姿态测量中的应用[J].北京理工大学学报,1999,19(3):36l-363.
[5]高峰,张合.基于基准角和补偿角的常规弹药滚转角磁探测算法研究[J].探测与控制学报,2008,30(5):ll-15.
[6]李汀,赵成刚,卜雄洙.基于磁传感器组合的高旋弹横滚角测量方法[J].南京理工大学学报,2009,33(3):320-324.
[7]焦叙明.时频分析及其在地震资料处理分析中的应用[D].青岛:中国海洋大学,2007:15-20.
[8]丁克良,沈云中,欧吉坤.整体最小二乘法直线拟合[J].辽宁工程技术大学学报,2010,39(1):44-47.
[9]王米娜,杨建华,王晗,等.最小二乘法在电子鼻动态信息融合中的应用[J].传感技术学报,2005,18(3):580-583.
[10]都强,杭柏林.最小二乘法在多传感器测量标定中的应用[J].传感技术学报,2005,18(2):244-246.
[11]尹秉奎,黄镇昌.过零点位置比相在齿轮误差信号处理中的应用[J].现代制造过程,2007(2):92-94.
[12]吕游,刘吉臻,赵文杰,杨婷婷.基于分段曲线拟合的稳态检测方法[J].仪器仪表学报,2012,33(1):194-200.
[13]王雨时.旋转弹丸外弹道自转角速度衰减规律半经验公式[J].探测与控制学报,2003,25(1):1-6.
