大位移磁致伸缩传感器的弹性波建模与分析*

代前国，周新志

(四川大学电子信息学院，成都610065)

位置测量方式很多，随着测量精度和测量环境的工业性要求，传统位置传感器不能满足要求。磁致伸缩位移传感器是一种新型的位移传感器，其有测量精度高，测量位移大，测量非接触[1－4]，适用于恶劣环境中对位置的测量。广泛应用于石油，航空，水利，数控，自动化等工业环境中[5－7]。

目前，国内正处于对该传感器的自主研究和设计阶段，该传感器测量位移不是很大，大位移传感器主要靠进口。研究主要集中在传感器材料和传感器系统集成方面，该传感器测量位移不大，在5 m以内。由于该传感器涉及材料，力学，电磁学和信号处理交叉学科，难以对传感器建立一个系统的数学模型。本文主要对基于FeGa材料为波导丝的弹性波进行建模和分析。根据波导材料的动力学原理，建立了FeGa磁致伸缩波导丝的弹性波振动方程[8－9]。同时根据磁致伸缩材料的魏德曼效应(Wiedman Effect)和Jile-Atherton磁点耦合模型给出磁致伸缩位移传感器弹性波信号的模型以了解弹性波的传递特性[10－11]。

1 磁致伸缩位移传感器原理

磁致伸缩位移传感器系统主要由脉冲发生电路，波导丝和弹性波信号接收电路3部分组成，组成系统如图1所示。发射端脉冲发生电路向磁致伸缩波导管施加一个电流脉冲Ip，该电流脉冲沿磁致伸缩波导管向另一端传播。此周期电流脉冲将产生一个环绕磁致伸缩波导管的环向磁场Φc，同时在波导管外部环形永久磁铁产生一个沿波导丝轴向的稳恒磁场Φr。当环向磁场Φc遇到轴向稳恒磁场Φr时，产生叠加并形成一个螺旋形的合成磁场Φ。根据磁致伸缩材料的磁致伸缩效应，在合成磁场Φ的作用下，将使磁致伸缩波导管产生瞬时局部扭转变形，从而形成扭转超声波[3，5]。该超声波以恒定的速度v向两边传播。

图1 磁致伸缩位移传感器工作原理

同时，在信号检测线圈端，由于魏德曼效应可以检测出弹性波信号，检测信号电压由式(1)可得。

其中εo是感性线圈感应电动势，N是线圈匝数，S是线圈横切面的有效面积，dB/dt是磁场的变化率。测量输出脉冲信号和接受信号的时间差T，则可以根据L=vT测量出永久性磁铁的距离。

2 弹性波的振动模型

圆柱型FeGa材料的波导丝具有连续性，均匀性，各向同性，小变形等特性。以永久性磁铁的位置为中心原点建立坐标，如图2所示，分析和建立波导丝振动力学方程。

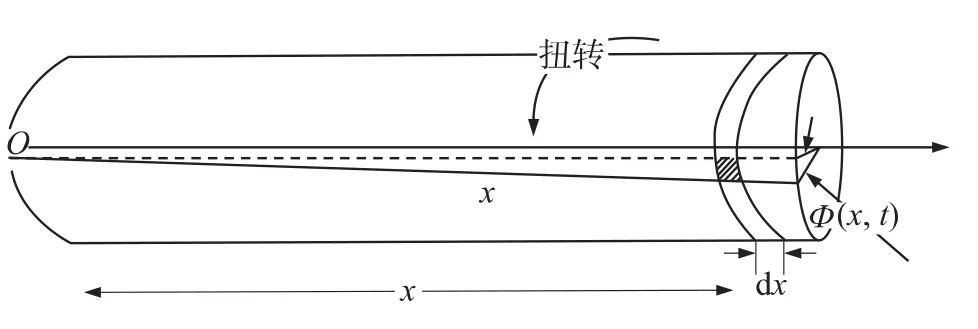
图2 磁致伸缩材料波导丝的扭转波产生

设波导丝的单位质量为ρ，圆切面对其中心的极惯性矩为I，材料的弹性模量为E，波导丝轴的横截面在扭转过程中，x截面的转角位移用φ(x，t)表示。在x截面处取出一小段dx作为隔离体，如图2所示，列出受力平衡方程ΣM=0:

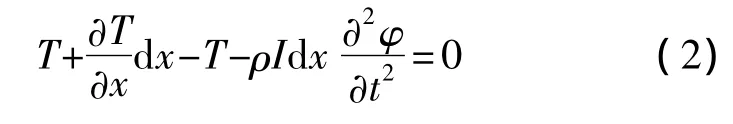
即是:

式中:T为x截面的扭矩。根据材料力学中圆轴扭转的扭转角公式，有

将式(4)代入式(2)，可得

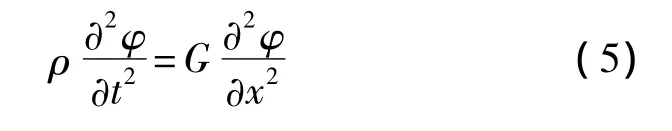
3 磁机耦合方程

因为磁致伸缩材料伸缩一般很小，同时接收线圈长度也很小，磁致伸缩过程主要与磁场和材料的机械性能相关，其中线性主要有两个线性磁机耦合方程[11－12]:

其中ε和σ是FeGa材料纵向应力和轴向应力，E是杨氏弹性模量，μσ是在磁场作用下的相对磁导率，方程中dσ和d分别是磁致弹性波耦合系数和逆磁致弹性波耦合系数，其分别有式(9)和式(10)所示定义。同时方程(6)反映了磁致伸缩材料FeGa的弹性特性(σ/E)和磁致特性(dH)，方程(7)包含了由于弹性应力作用下磁致伸缩效应直接产生的磁化现象[13]。

要使如上磁机耦合方程成立，要假设方程中所涉及磁致伸缩，逆磁致伸缩，弹性波和磁化等有关变量都是线性相关的，因此要求在接收线圈处的磁致伸缩区域力学特性是线性的。同时由于电流的趋肤效应忽略涡流和磁致伸缩材料的磁滞效应。

在弹性波传递过程中，根据逆磁致伸缩效逆磁致伸缩效应和磁机耦合关系[14]如下，

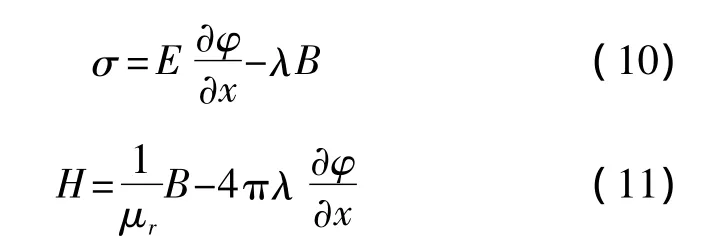
其中λ是磁致伸缩系数。∂φ/∂x是磁致伸缩应力。等式中磁场强度已知，在给定线圈参数情况下，磁场可以计算出来。根据材料力学 T=σ和式(5)、式(10)和式(4)3个等式可得

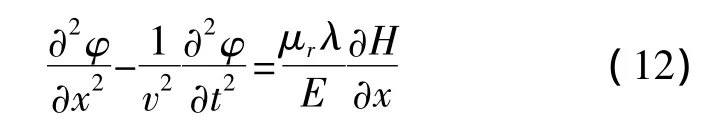
该方程是一个二次偏微分方程，解比较复杂。在实验中，波导丝直径很小，极惯性矩I变化小，视为单位极惯性矩。而只考虑在永久性磁铁处出现最大的磁致伸缩效应，波导丝其他点的磁致伸缩不考虑，但是由于永久性磁铁和脉冲合成的磁场H是不均匀分布的，可用H(x，t)表示。同时，由于实验中使用的时周期性大电流脉冲I(t)，根据傅里叶变换

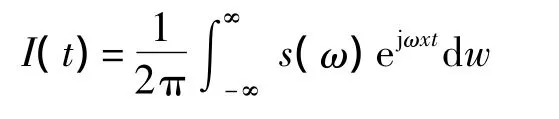
其中s(ω)是I(t)的傅里叶变换，周期信号I(t)可有一频率不同的解析信号线性组合而成，因此，假设φ(x，t)=φ(x)ejwt，为了方程计算更加简单，假设H(x，t)=H(x)ejwt，因此方程(12)可化简为

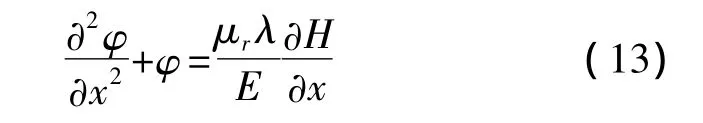
该方程是一个二次差分方程，其通解可表示为

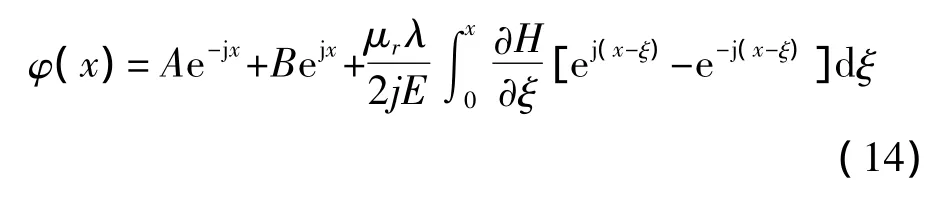
等式中A，B固定振荡部分为待定系数，由于磁致伸缩效应和后面线圈对信号的接收，只考虑强迫振荡则有:

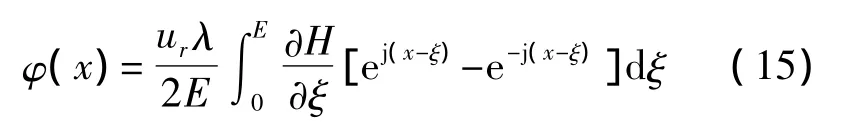
4 线圈接收信号输出模型

考虑弹性波信号接收线圈，如图3所示，线圈开路，线圈不会产生电流，从而不存在磁场强度H，影响磁感应强度的主要因素为磁致伸缩效应的应变σ(∂φ/∂x)，即式(11)可化简为

该方程表示接收线圈在开路情况下的逆磁致伸缩机磁耦合方程[15]。然线圈每单位长度的线圈匝数为n，截面有效区域为 s，取微小的 dx长度，匝数为ndx。则通过ndx的磁通量

将式(16)代入得

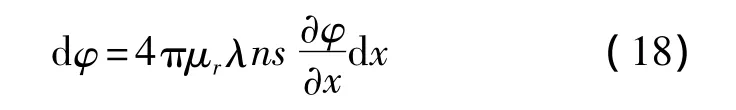
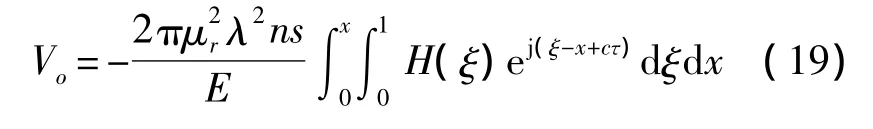
同时在永久性磁铁位置处有合成磁场

Hr为永久性磁场，HI为脉冲电流磁场有HI(x，t)=kIC(x)，Hr(x，t)=Hrf(x)。其中k为电流与磁场耦合系数，近似为 k=1/(2πr)(r为波导丝半径);c(x)，f(x)位置分布函数。

由式(19)和式(20)可得

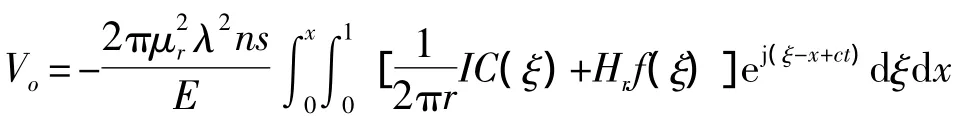
实际中，必须考虑信号能量的衰减，假设衰减函数为g(x)，g(x)是位置衰减型的函数。则有电压输出电压函数

图3 接受信号线圈

由电压输出式(21)可知，弹性波输出电压主要受以下因素影响;磁致伸缩材料的磁致伸缩系数λ，波导丝半径r，接受线圈匝数n，和截面的有效面积s，材料的相对磁导率μr和输入电流I(t)和永久性磁场在环向的磁场Hc(Hc为Hr在环向的磁场最大值)等影响。如果线圈特性和波导丝材料都固定的情况下，决定输出电压的因素主要是脉冲电流，I(t)→Vo，Vo∝1/x，即x位置的增加信号输出幅度减小。

5 实验结果与分析

数学模型是建立在理想条件下的，其弹性波的动力学模型是自由振荡模型，实际试验中不可能是这样。实验中，如图4激励电流脉冲频率为250 kHz，脉冲宽度为 28 μs。

图4 激励脉冲波形

波导丝用FeGa材料，长度为2 m左右，波导丝直径约为5 mm。信号检测线圈匝数约为300匝，经过信号放大，信号滤波后，不同位置的信号幅度波形检测如图5(a)所示。

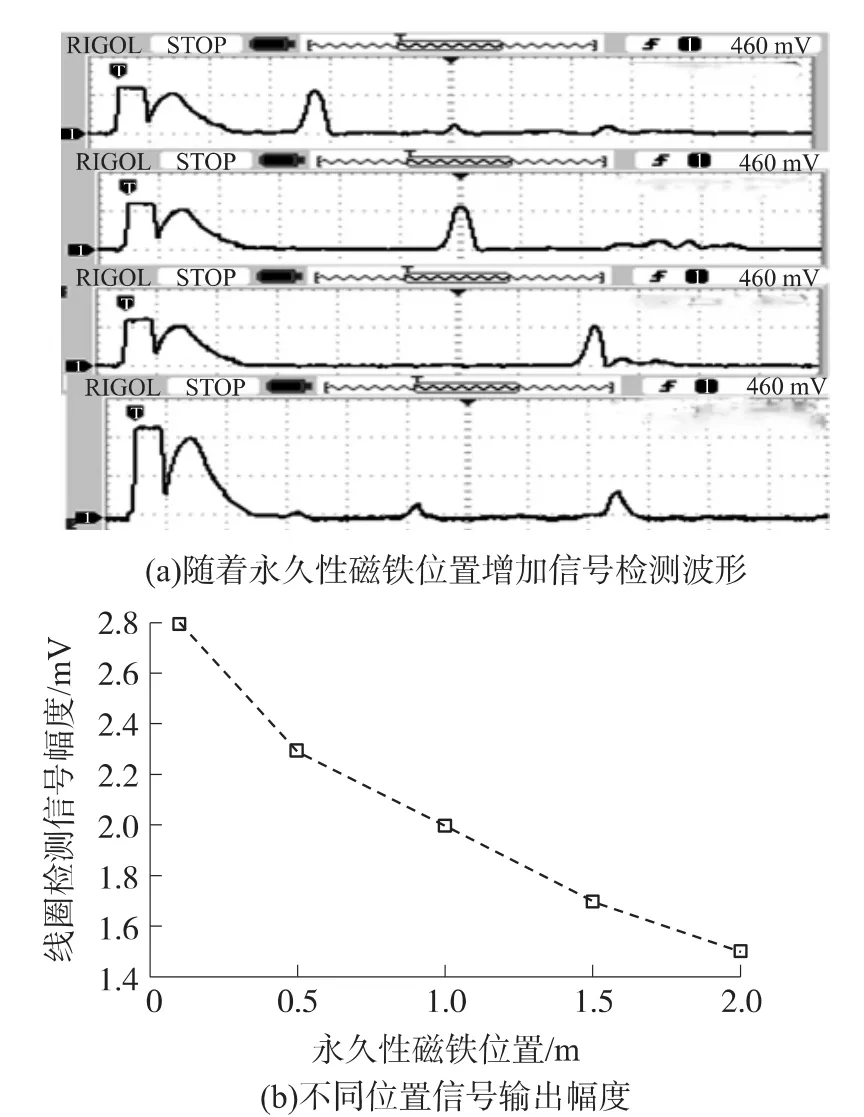
图5

由实验结果图5(a)、5(b)所示，在理论模型基础上，以FeGa材料为核心搭建的实验系统很好实现了对信号的检测。实验中，以2 m为测量量程，测量了4个位置点原始输出信号，实验结果如图5(b)所示。实验测量时检测信号幅度小，在mV级，同时随着距离增加输出信号存在二次函数衰减。位置不变情况下，不同输入电流对输出信号幅度影响，如图6所示，脉冲电流越大输出信号幅度越大，成正比例关系。同时从图5(b)可以看出，该传感器有较好的线性测量特性;试验中通过光栅尺对传感器进行标记，该传感器精度能达到20μm。

图6 不同电流输入的输出信号幅度

实验结果显示，输出信号幅度与输入电流成正比、与测量位置成反比。由于系统误差和人工误差和忽略了环境干扰对测量信号的影响，通过多次重复测量减少误差，使得实验结果和预期的结果基本吻合，说明了该弹性波模型的可行性。

6 结论

FeGa是一种磁致伸缩系数较大的材料，以其作为波导丝能很好实现磁致伸缩位移传感器功能。磁致伸缩位移传感器系统是多学科交叉，建立统一模型比较复杂，很难对该系统进行定量分析。本文通过对波导丝的振动方程和材料力学方程和磁机耦合方程3个方面考虑，推导出了信号输出模型是距离的变化，并假设信号的衰减。通过实验获得信号输出，验证信号输出与模型的一致性。建模过程中，由于模型的复杂性，如温度特性、磁滞特性、剩磁特性等被忽略了，系统模型需要进一步提高，但该模型对磁致伸缩位移传感器的理论研究有积极意义。

[1]李春楠，卢云，兰中文，等．磁致伸缩位移传感器的研究进展[J]．实验科学与技术，2008，1(6):10－12．

[2]冯建，赵辉，刘伟文，等．陶若杰磁致伸缩位移传感器电路系统的设计[J]．电子测量技术，2010，1(33):11－13．

[3]Fernando Seco，José Miguel Martín，Antonio Ramón Jiménez．Improving the Accuracy of Magnetostrictive Linear Position Sensors[J]．IEEE Transactions on Instrumentation and Measurement，2009，3(58):722－728．

[4]姜建山，陈伟民．外力对逆磁致伸缩索力传感器影响研究[J]．传感技术学报，2009，3(22):439－441．

[5]颜庆伟，赵玉龙，蒋庄德．磁致伸缩液位传感器的电路设计及性能分析[J]．传感技术学报，2008，5(21):778－780．

[6]葛春亚，贾振元，王福吉，等．超磁致伸缩力传感器及其实验研究[J]．仪表仪器学报，2011，6:3－5．

[7]Liu Huifang，Jia Zhenyuan，Wang Fuji．et al．Study on the Design Method of Giant Magnetostrictive [C]//Beijing， China，Proceedings of the IEEE International Conference on Mechatronics and Automation，2011．1098－1103．

[8]李东，袁惠群．超磁致伸缩换能器耦合磁弹性模型与振动特性分析[J]．固体力学学报，2011，4(32):366－370．

[9]Woochul Kim，Yoon Young Kim．Design of a Bias Magnetic System of a Magnetostrictive Sensor for Flexural Wave Measurement[J]．IEEE Transactions on Magnetics，2004，5(40):3331－3338．

[10]Marcelo J Dapino，Ralph C Smith，Alison B Flatau，et al．Structural Magnetic Strain Model for MagnetostrictiveTransducers[J]．IEEE Transactions on Magnetics，2000，3(36):545－556．

[11]Weng Ling，Wang Bowen，Sun Ying，et al．Model and Experiment of Giant Magnetostrictive Vibration Sensor[C]//China，11th International Conference on Electrical Machines and Systems，Wuhan，2008．4092－4095．

[12]崔旭，何忠波，李冬伟，等．超磁致伸缩致动器建模研究综述[J]．兵器材料科学与工程，2011，4(34):90－93．

[13]王峥，常晓明，脇若弘之．长线磁致伸缩位移传感器的磁极化强度模型[J]．传感技术学报，2010，8(23):1075－1078．

[14]Affanni A，GuerraA，DallagiovdnnaL，etal．Design and Characterization of Magnetostrictive Linear Displacement Sensors[C]//CoMo，Italy，Proceedings of the 21st IEEE Instrumentation and Measurement Technology Conference，2004．206－209．

[15]Wan J G，Or S W，Liu J M，et al．Magnetoelectric Properties of a Heterostructure of Magnetostrictive and Piezoelectric Composites[J]．IEEE Transactions on Magnetics，2004，4(40):3042－3044．