电子罗盘安装误差标定与补偿方法研究*

范成叶，李 杰，2* ，陈文蓉，景增增，刘 俊，2

(1．中北大学电子测试技术重点实验室，太原030051;2．中北大学仪器科学与动态测试教育部重点实验室，太原030051)

随着现代科学技术的进步，许多工业领域对载体航向姿态测量精度的要求越来越高。航向导航一般有陀螺仪航向、无线电航向和磁航向，在这三种航向设备中，陀螺航向仪的成本比较高，无线电航向仪受到电磁的干扰比较大，因此在导航中受到一定的限制，而电子罗盘以其体积小、功耗低、误差不随时间累积等优点广泛应用于磁航向领域。在不考虑制造误差等其他误差的情况下，电子罗盘在实际安装使用过程中受加工技术和工艺的限制不可避免的存在安装误差，导致其测量结果误差较大、精度低，为了获得高精度、高可靠性的导航信息，就必须对传感器进行有效的误差标定与补偿。Honeywell公司推出的智能电子罗盘模块HMR3300，以HMC1022型双轴磁传感器为基础，可以提供对地磁场的X、Y、Z三轴磁场传感功能，受地磁场的作用而指北[1];文中以HMR3300为例，在分析电子罗盘安装误差角产生机理的基础上，对电子罗盘安装误差标定和补偿方法进行研究。

1 安装误差模型建立

1．1 安装误差产生机理分析

电子罗盘在运动载体上以捷联方式安装，在实际安装过程中，受加工技术和工艺的限制，其三个测量轴构成的输出坐标系不可能与载体坐标系完全重合或平行[2]，总存在一定的安装误差角如图1。图1中，X0、Y0、Z0分别表示与载体坐标轴平行的三个轴，即电子罗盘安装于载体上时理想的三轴指向;X、Y、Z分别表示电子罗盘安装在载体上时，三个轴的实际指向;α表示X与X0之间的夹角;β表示Y与Y0之间的夹角;α和β称为电子罗盘的安装误差角[3－4]。

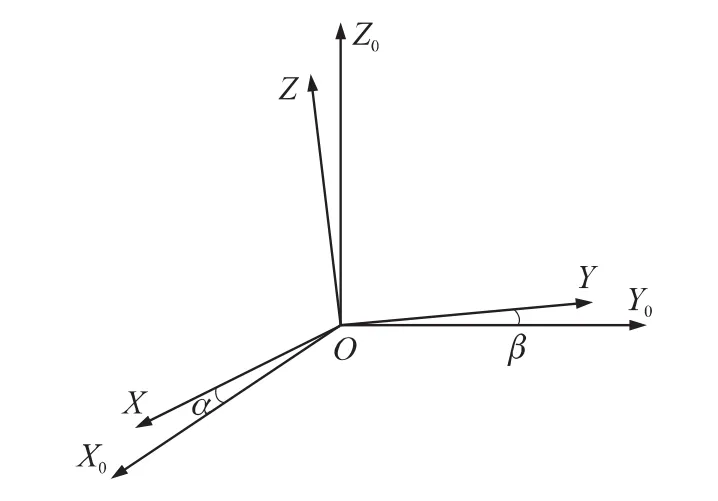
图1 不正交安装误差角示意图

1．2 安装误差模型的建立

电子罗盘安装在载体上时，一般会同时存在两个安装误差角[5]。首先讨论存在单一安装误差角的情况，通过分析对磁测数据的影响，提出单一安装误差角的测量方法，并在此基础上衍生出两个安装误差角的测试方法。

电子罗盘存在单一安装误差角α时，三个测量轴与载体坐标系之间的关系如图2所示。

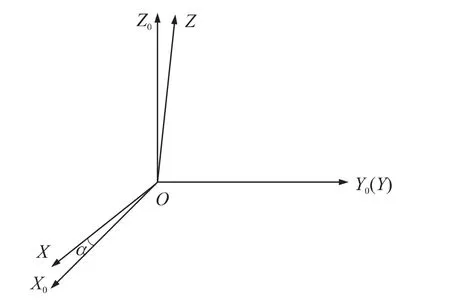
图2 单一安装误差角(α)示意图

图中，OX0Y0Z0表示载体坐标系，OXYZ表示电子罗盘的三个测量轴所在的坐标系。当存在单一安装误差角α的时候，X轴与X0轴不再重合，二者之间有一个角度，即安装误差角α。OX0Y0Z0坐标系到OXYZ坐标系的变化可看作是前者绕Y0轴旋转角α使得Y与Y0重合，X落在X0OZ0面内得到。此时，则电子罗盘X轴向的实际输出值为X=X0cosα+Z0sinα，Z 轴向实际输出值为 Z=－X0sinα+Z0cosα，罗盘在XOY0面上旋转一圈时，可以采集到多组三维磁场数值，采用最小二乘法进行直线拟合可得出α=－tan(dZ/dX)。

同理，当Y轴方向存在单一误差角时，Y轴与Y0轴的夹角为β，且Y轴在Y0OZ0面内，电子罗盘在X0OY面上绕Z轴旋转一圈时，可以得到 β=－tan(dZ/dY)。

当同时存在两个安装误差角时，载体坐标系相对于电子罗盘测量轴的示意图如图1示。在仅考虑安装误差的情况下，从电子罗盘输出坐标系OXYZ到载体直角坐标系OX0Y0Z0，可以通过连续旋转得到，即OXYZ绕X轴和Y轴分别转动两个微小的角度α、β可以转换到载体坐标系OX0Y0Z0，坐标变换方程为:

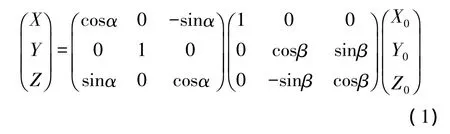
电子罗盘安装后，安装误差角就确定不变了，若能准确标定该安装误差角α、β就可以对电子罗盘输出的测量值进行安装误差补偿;一般的安装工艺可以保证各安装误差角在±20'之内，安装误差角α、β非常小，因此，化简方程1可得安装误差补偿方程如下:

1．3 安装误差角的求解

安装电子罗盘过程中，由于两个角α、β的值很小，求解安装角时可以采用忽略其中一个求解另外一个的方法。求解α角时，忽略β角，采用单一误差角的求解方法，得到α=－arctan(dZ/dX);同理当忽略α角时，可以得到β=－arctan(dZ/dY)。

同时存在两个安装误差角α、β的情况下，X、Z方向磁场强度在XOZ面上由不平行X轴的直线畸变成椭圆，并且椭圆关于该直线成轴对称性，畸变是由于另外一个安装误差角β引起的，前面阐述了求取安装误差角采用忽略其中一个求取另一个的方法，可以采用最小二乘法拟合直线的方法[6－7]，求出斜率进而解算出α。

1．4 仿真分析

通过理论仿真验证1．3中论述的安装误差角求解方法的正确性，假定电子罗盘在水平放置时测得的三轴磁场强度为(1 348 454．3 －1 718．6)，当存在两个安装误差角时，取 α=5°，β=10°，则平面内旋转一圈三轴磁场强度如图3、图4所示。

从图中可以看出，XOZ面和YOZ面上的磁场强度由平行于横坐标的直线变为椭圆[8]，通过最小二乘法拟合得到安装误差角 α1=4．924 4°，β1=9．923 7°，接近事先设定的数值，根据式2对三维磁测数据进行安装误差角补偿，得到新的磁测数据，继续使用上述方法 第 二 次 计 算 安 装 误 差 角[9]，得 到 α2=0．0756°，β2=0．0760°。将两次拟合计算的结果对应相加，得到最终安装角误差 α=5°，β=9．9997°，与预先设定的安装误差角基本相等。

根据式(2)对安装误差角补偿，得出补偿前后三轴磁场强度对比如图5、图6所示。

图5、6中所示，安装误差角补偿后的磁测数据由畸变的椭圆变为直线，与原始的数据相互重合，Z轴方向的磁场强度保持不变，表明该求解安装误差角方法是正确而且有效的。

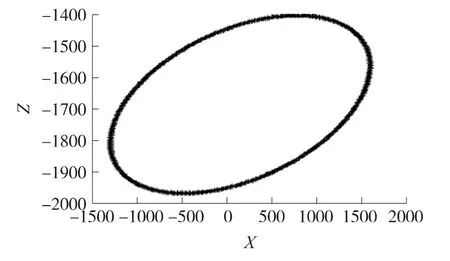
图3 X、Z方向磁场强度

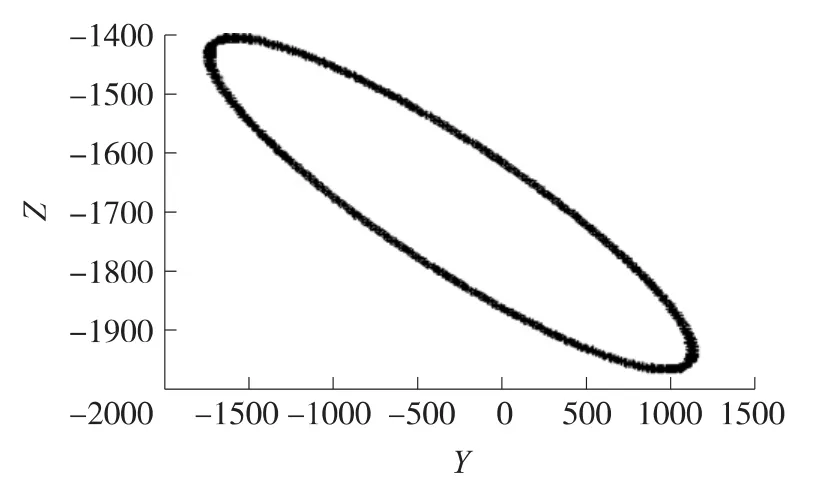
图4 Y、Z方向磁场强度

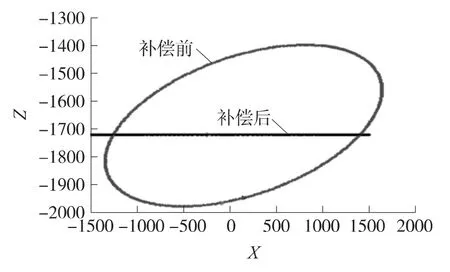
图5 X、Z方向磁场强度补偿前后对比

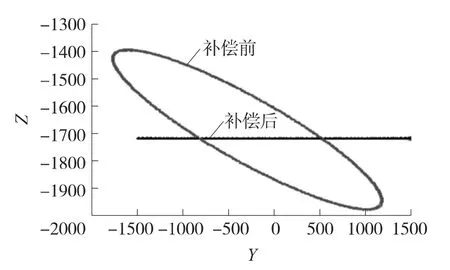
图6 Y、Z方向磁场强度补偿前后对比

2 安装误差角的标定

2．1 关于标定平面的讨论

上述方法的推导是建立在载体在水平面上旋转的基础上得到的，但在实际的操作中，水平面的要求限制了该方法的实施，需要讨论在任意平面上是否也可以采用该方法标定和计算安装误差角。

假设电子罗盘三测量轴两两正交且不存在灵敏度误差和零偏误差，即实际输出为理论值，载体在任意平面上，电子罗盘与载体之间不存在安装误差，此时电子罗盘绕Z轴旋转360°，由于Z轴始终与平面呈90°的夹角，故而Z轴方向的磁场分量保持不变，X轴和Y轴方向磁场分量为正弦变化，且二者之间相互正交，这与载体安装于水平面上的情况是类似的。当存在安装误差角的情况下，载体在水平面上旋转一圈相应的三维磁传感器在XOZ面和YOZ面上磁场强度的分布情况由直线畸变成椭圆，与载体在水平面上磁场数据的变化规律相同，故§1．2中推导的安装误差角标定和计算方法适用于任意平面。

2．2 标定方案设计

①选择磁环境相对较洁净的地方，任意选取一个平面。将电子罗盘在该平面上旋转360度，实时采集三个轴方向上的磁场强度，从而获得一系列丰富的测量值;②根据Y、Z两个方向的磁场强度，采用最小二乘法拟合直线，计算出直线的斜率，反正切解算出β1;③根据X、Z两个方向的磁场强度，解算出α1;④根据方程2对安装误差角进行补偿，根据上述方法再次计算安装误差角α2、β2;⑤最终解算出安装误差角 α=α1+α2，β=β1+β2;⑥解算出安装误差角补偿后三维磁场强度(X，Y，Z)。

最小二乘法拟合直线求解出的安装误差角是实际安装误差角的一个近似值，可以采用逐步逼近的方式进行精确标定;对前一次求解的安装误差角进行补偿后再次求取安装误差角，多次求取的安装误差角之和可以无限接近实际安装误差角。

3 试验验证

为了验证该安装误差角标定与补偿方法的正确性和有效性，使用HMC3300进行试验验证，因为铝材料对地磁场没有影响[10－13]，将电子罗盘安装在铝制矩形壳体内，此时安装误差主要是由于电子罗盘固定于壳体中时，X轴、Y轴所构成的平面与壳体下表面不平行引起的，根据前文所述方法在不同倾角平面上进行了电子罗盘安装误差角标定试验，得出结果如表1所示。

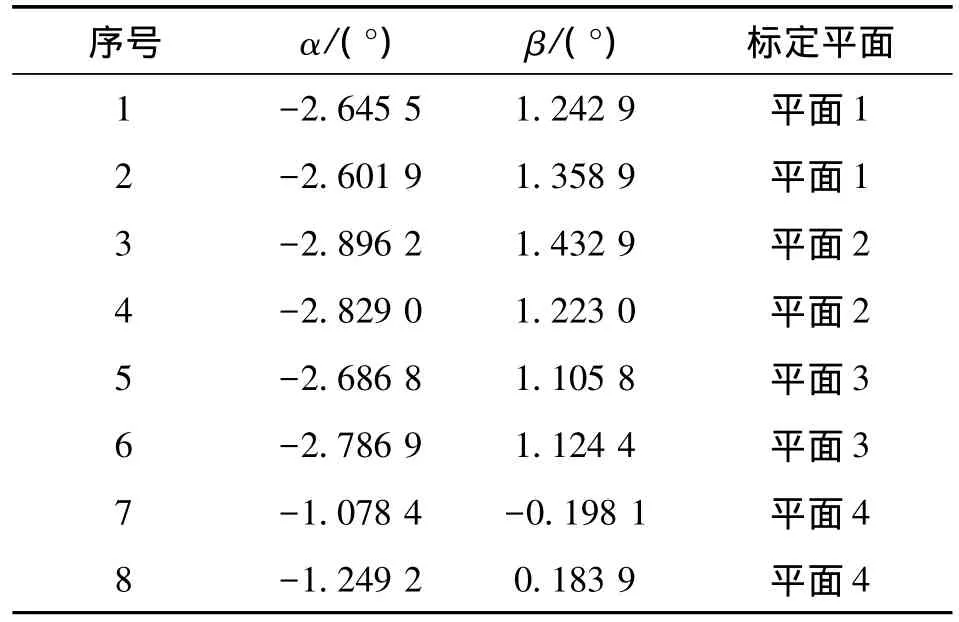
表1 安装误差角标定结果

表1中，在平面1－平面3上标定得到的安装误差角基本一致，而在平面4上标定得到安装误差角与其余三个平面标定结果相差较大，以下通过分析磁场强度来探究原因，4个平面内磁场强度变化分别如图7～图10所示。

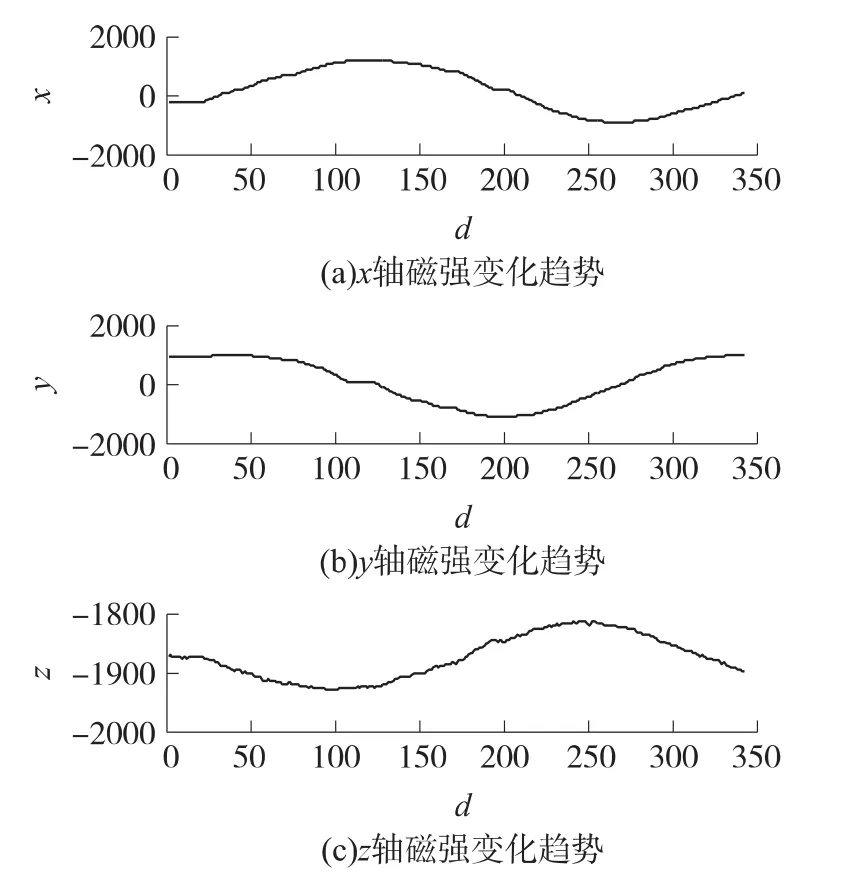
图7 磁场强度变化(平面1)

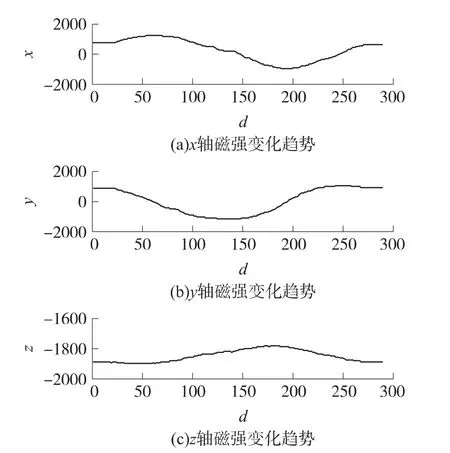
图8 磁场强度变化(平面2)

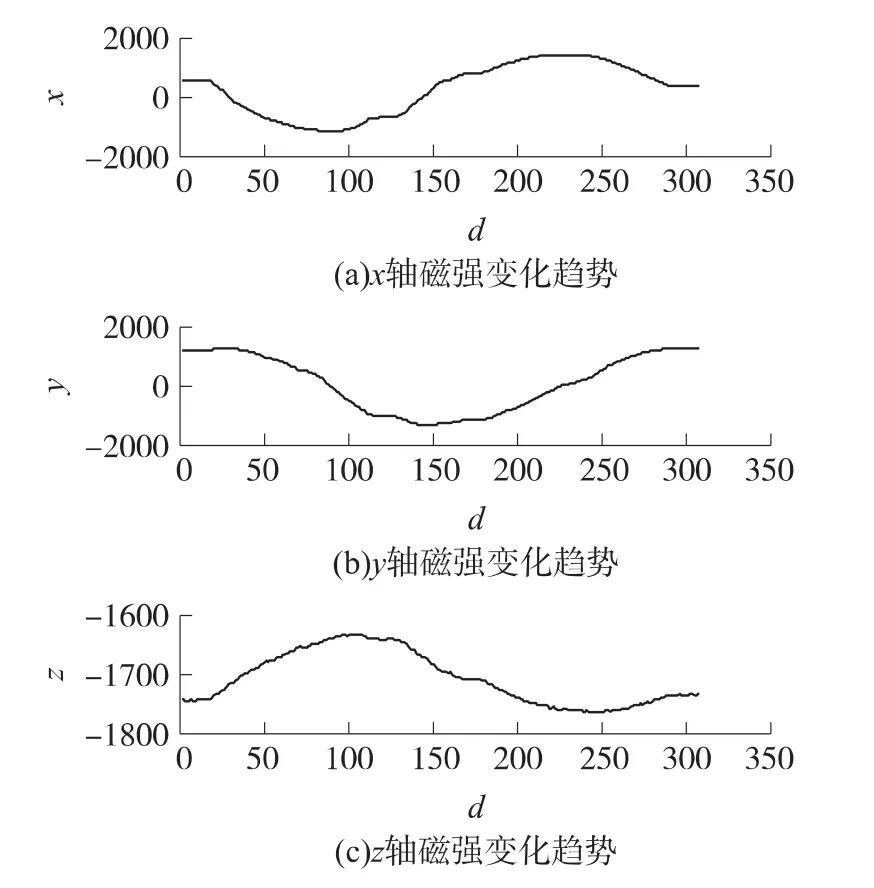
图9 磁场强度变化(平面3)

图10 磁场强度变化(平面4)

可以看出平面4上采集的磁场强度变化明显小于其余三组测量结果，且Z轴的磁场强度绝对值大于其余三组;已知当标定平面与地磁场矢量平行时，X轴、Y轴方向的磁场矢量和接近于零，旋转一圈，两轴由于安装误差引起的磁场变化量与磁传感器本身测量误差接近，不能很好地反映安装误差角引起的各个轴上的磁场变化;故而，出现以上结果的原因是平面4与地磁矢量场接近平行，导致标定所得到的安装误差角有偏差。同理，若标定平面与地磁场矢量垂直时，由于Z轴方向磁场矢量变化小，所得到的安装误差角与实际也会有一定的偏差。故标定平面的选择最好是与地磁矢量倾角为45°，该情况下测得的安装误差角偏差最小。

选取平面1标定的安装误差角进行补偿，补偿前后磁场测量数据对比如图11所示。

图11中，横坐标为采样点，纵坐标为Z轴方向磁场强度，蓝色为安装误差补偿前Z轴磁场强度变化曲线，红色为安装误差补偿后Z轴磁场强度变化曲线。从图中可以看出补偿后Z轴磁场强度变化幅度减小，补偿效果明显。

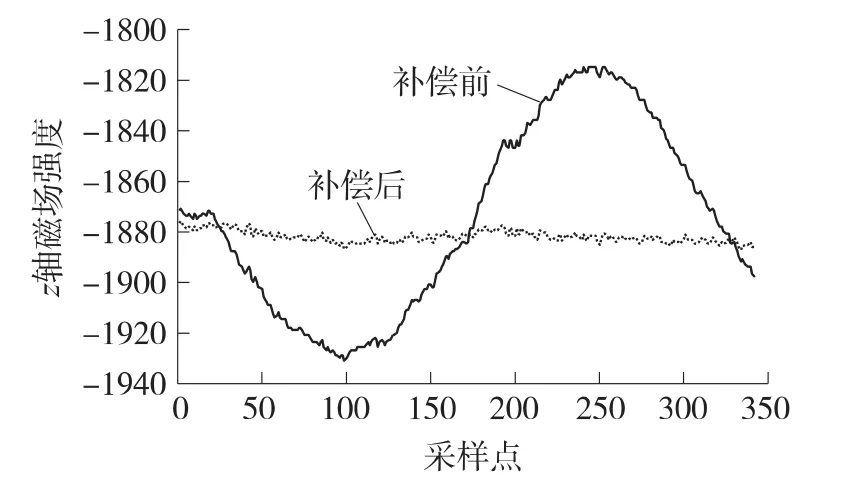
图11 安装误差角补偿前后磁场数据变化

4 结束语

电子罗盘在运动载体上以捷联方式安装，在实际安装过程中，受加工技术和工艺的限制，其三个测量轴构成的输出坐标系不可能与载体坐标系完全重合或平行，总存在一定的安装误差角。对电子罗盘的安装误差进行准确的标定和补偿是保证地磁导航系统测量精度的基本前提，本文分析了电子罗盘安装误差产生机理，提出了忽略单个安装误差角求取另外一个误差角的方法，推导出了基于最小二乘拟合直线求解角度的安装误差角标定补偿方法，标定补偿过程简捷、方便、易于实现。仿真分析试验和不同平面下的标定试验表明安装误差补偿效果明显，能够为地磁导航系统提供准确的信息，该方法能够广泛应用于电子罗盘安装误差角的快速标定和有效补偿。

[1]杜英，李杰，孔祥雷，王博，于希宁．无航向基准条件下电子罗盘的误差补偿方法研究[J]．传感技术学报，2010:1285－1288．

[2]张晓明．地磁导航中磁测误差补偿技术研究[D]．北京航空航天大学．2009．

[3]杨晓东，王炜．地磁导航原理[M]．北京:国防工业出版社，2009．9:67－80．

[4]Li Q，G．Griffiths J．Least Square Ellipsoid Specific Fitting[C]//IEEE，Proceedings of the Geometric Modeling and Processing 2004．Beijing:IEEE，2004:335－340．

[5]肖昌汉．三分量磁传感器非理想放置时磁场数据的分析方法[J]．海军工程学院学报，1996，76(3):7－11．

[6]李仁，陈希军，曾双庆．旋转式捷联惯导系统误差分析[J]．哈尔滨工业大学学报，2010，42(3):368－372．

[7]Hepner D，Harkins T．Determining Inertial Orientation of a Spinning Body With Body-fixed Sensor[R]．ARLTR－2313，2001:7－11．

[8]李秉玺，赵忠，孙照鑫．磁阻传感器的捷联式磁航向仪及误差补偿[J]．传感技术学报，2003:191－194．

[9]Grammalidis N，G．Strintzis M．Head Detection and Tracking by 2-D and 3-D Ellipsoid Fitting[C]//IEEE Computer Graphics International．Geneva:IEEE，2000:221－226．

[10]郭秋芬，谢莉莉，谢仕民．磁航向计在导航中的应用研究及其误差补偿与修正[J]．战术导弹控制技术，2009，31(1):41－45．

[11]李书华，邵勇．HMR3300电子罗盘在车载设备上的使用[J]．光电子技术应用，2010(6)13－17．

[12]Xensor Integration Corporation．Earth Magnetic Filed Sensor XEN－1200[Z]．2007．

[13]闫蓓，王斌，李媛．基于最小二乘法的椭圆拟合改进算法[J]．北京航空航天大学学报．2008，34(3):295－298．