概率课程教学技巧探讨

阮传同

（周口师范学院 数学与信息科学系，河南 周口466001）

概率论［1］作为主要研究随机现象的基础理论，越来越受到社会各界的关注，已经成为高等院校大部分专业必修的基础课.随着中学新教材的改革，也把概率论的有关知识纳入中学教材，使概率论在师范院校的重要性日益突出.然而，由于此门课程处理问题的思想方法与学生以往学过的数学课程有一定差异，导致学生对它望而生畏，学习起来感到束手无策，找不到学习感觉.作为一线教师，如何改变这种现状，如何培养学生学习概率的积极性，进而提高教学质量，就成为迫切需要解决的问题.为了提高学生学习兴趣，也有学者做了大量的探索［2-4］.然而，大学生的心理已经成熟，已不同于小学初中生.在授课时，除了语言精练、风趣，紧紧与生活相联系外，还更需要提高教学技巧，改革教学方法.本人根据多年教学实践，针对不同情况，给出一些教学策略、技巧，供同仁参考.

1 小题大做

对于简单的问题，学生自己就可轻松做出来，不需要任何人的讲解，但有时提不起学生的兴趣.如何让学生耳目一新呢？简单的问题复杂化.采用复杂的方法来解决简单问题，学生顿感好笑之余，却能很好地理解并掌握此复杂方法，为以后用复杂的方法解决复杂问题做好铺垫.

例 有一批产品，甲厂生产的60件，其中10件是次品；乙厂生产的40件，其中5件是次品.现从这批产品中任取一件，求取得的产品是次品的概率.

解记A1＝ “取到的为甲厂的产品”，A2＝“取到的为乙厂的产品”，A＝“取到的为次品”，则由A1∪A2＝Ω知

又因A1A⊂A1，A2A⊂A2，A1∩A2＝ Ø，所以，A1A和A2A互不相容，故

这个简单的问题，用的其实是概率论上著名的全概率公式，无形中，学生已经提前接触到了.未雨绸缪，以后学习时，也不会让学生感觉太突然，太陌生.同时，也避免了让复杂的公式成为无源之水、无本之木.

2 欲擒故纵

分布函数是一个有用的概率论工具，就是通过它，微积分工具和概率论才联系在了一起.但是分布函数非常难理解，学生望而生畏.有关这方面的题目，学生容易做错.怎么办？找一个看似简单的问题，让他们大胆地去猜测结果，天马行空，各抒己见.时机成熟后，再一个一个地驳倒他们，把他们拉回到现实，让学生陷入到山重水复疑无路的地步.学生碰壁后，都急切地盼望着正确答案，在大家的等待中给出严格的做题过程.

例设X为连续型随机变量，其密度函数为

且Y＝2X，求Y的密度函数.

这是一道有关分布函数应用的概率题，学生靠直觉最容易做错.利用密度函数的规范性，可以指出猜测的一些结果为什么是错的.但什么是正确的，学生还很茫然.正确做法如下：

解因ΩX＝ （0，1），所以，ΩY＝ （0，2）.故

当y≥2时，FY（y）＝P｛Y≤y｝＝1.

又因PY（y）＝F′Y（y），所以，

解得有理有据，没想到分布函数还有如此的妙用，学生顿时有了一种柳暗花明又一村的喜悦，无不对分布函数刮目相看.

3 独辟蹊径

讲课时，一定要把课本讲活，不能照搬课本.特别是难理解的问题，照本宣科，会让学生听得一脸雾水.这就要求寻找其他方法来解决，找出符合口味的、适合学生实际的、不让学生失去信心的方法来.

例若X～N（0，1），求X的特征函数φ（t）.

解因，所以，，故

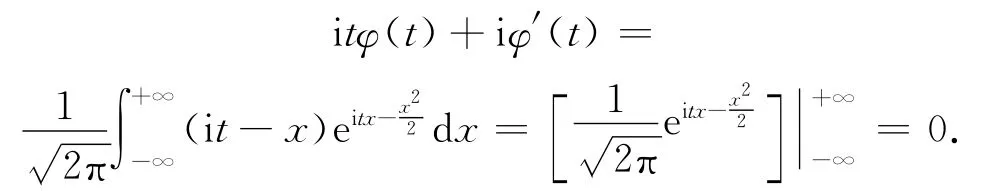
因此，φ（t）满足的常微分方程为

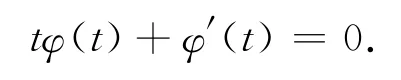
即

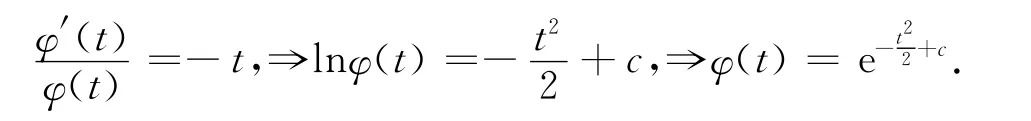
又φ（0）＝1，所以，c＝0.因此，X的特征函数为.

部分教材，对于X～N（0，1）时X的特征函数的求法虽多种多样，但大都很难理解，甚至有的知识点学生根本就没接触过.此外，有时省略比较多，学起来难上加难.如果不走寻常路，独辟蹊径，构造一个常微分方程［5］，用常微分方程的知识来解决这个概率问题，不失一种让学生眼前一亮的方法.学生做梦也不会想到，学过的常微分方程还有这方面的威力.

4 星火燎原

原本很重要的一个知识点，就因为它小，往往被学生忽略.这时，为了显示它的重要性，引起学生们注意，把它展开、放大，一丁点的火星要让它燃烧成一片天.

方差的值永远不会小于0，学生都是知道的.但由方差的计算公式推出的重要结论：随机变量平方的期望不会小于随机变量期望的平方，却往往被学生忽略.

例求证：.

证构造随机变量的分布列为

X x y P 1 2 1 2

则

又因E（X2）≥ （E（X））2，所以

推广：此方法可以证明不等式

一道高中的数学证明，用概率论知识来证明，看起来很新鲜，学生自然不敢再小看这个知识点了.

5 以逸待劳

学到概率论后面章节的时候，有些问题偏难，而且难以理解.若对于一个问题，巧妙地将条件略加改动，使之成为一个新问题，通过前后对照，则可以加深学生对问题的理解，激发学生学习积极性.

例有一人不小心掉进了一口井里，井下有三个洞口.第一个洞口经3小时可以出去，第二个洞口经5小时又返回原处，第三个洞口经7小时也返回原处.若此人每次等可能地选择一个洞口，求此人平均多久可以出去.

解记X＝i表示“此人第一次选择了第i个洞口”i＝1，2，3，Y＝ “此人出来的时间”.则随机变量X的分布列为

X 1 2 3 P 1 3______1 3______1 3___

于是，

故由重期望公式知

以上主要利用了重期望公式，如果通过这个例子还不太理解重期望公式的话，可以对原题稍加改编，把“此人每次等可能地选择一个洞口”改成“此人有思维地去选择洞口，不走回头路”，以逸待劳，让学生重做一遍，在减轻自己负担的同时，往往还会起到事半功倍的效果，何乐而不为呢？此时 ，

故由重期望公式知

就是说，无思维能力的人掉进去，平均15小时可以出去；而有思维能力的人掉进去，则平均9小时就可以出去.

以上是个人的一些看法，但若要灵活用到这一些技巧、策略，还需要学习概率论以外的一些知识.总之，视野越开阔，授课就会越轻松.对于学生，假以时日，再遇到一些问题，他们自己就可以去分析了.学生等学完了概率课，再回来复习，就有了一种不畏浮云遮望眼，只缘身在最高层的轻松之感.

［1］茆诗松，程依明，濮晓龙.概率论与数理统计教程［M］.北京：高等教育出版社，2004.

［2］杨云飞.如何培养学生学习概率统计的兴趣［J］.中国成人教育，2008（5）：170-171.

［3］郭花，刘洪霞，孙玉梅，等.概率教学中的趣味问题［J］.科技信息，2011（3）：550.

［4］聂铭.怎样在概率论的教学中激发学生的兴趣［J］.六盘水师范高等专科学校学报，2009，21（3）：66-68.

［5］王高雄，周之铭，朱思铭，等.常微分方程［M］.北京：高等教育出版社，2006.