在操作中理解 在体验中建构

史素珍

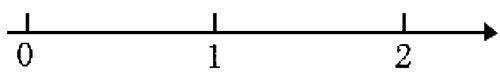
在特级教师许卫兵“认识小数”的课堂上，我和学生一起经历了小数意义的建构之旅。细细品味，许老师精巧的构思，灵动的教学机智深深触动了我。

片段展示：

片段一：从商品价格引入，揭示课题

（老师出示一些超市里的商品价格，有整数的，也有小数的。）

师：（点击出示：铅笔0.4元）铅笔用了多少钱？

生：4角。

师：我没有看到上面有4角啊？这个数以前见过吗？知道它是什么数吗？

生：小数。

师：（板书：小数）你怎么知道它是小数的？

生：老师以前讲过。

师：会读吗？

生：零点四。

师：有人说，小数非常好认，长得特别，你觉得呢？

生：因为它有小数点。

片段二：借助分数面积模型，初步理解小数的意义

师：你知道0.4元是多少钱吗？

生：4角。

师：（板书）有1元多吗？如果我把这个长方形看做1元，你能在这个长方形里把这个0.4元表示出来吗？

学生操作，交流汇报。

生1：我把它平均分成10份，再涂上4份。

师：为什么把它平均分成10份？

生1：因为1元有10角，所以把它平均分成10份。

师：1元有10角，平均分成10份，那1份就是——1角，4份就是——4角。有没有不一样的？

生2：他是分成了方块，我是分成了长条。

师：两种方法有什么相同的地方？

生2：都是平均分成了10份，都是涂了4份。

师：（小结，与学生一齐看屏幕）其实刚才几位同学的想法都是把它平均分成了10份，其中的一份就是——1角。0.4元是4角，也就涂了——4份，不就表示出来了吗？简单吗？

生：简单。

师：这么说，老师就想起来了，你们看看这个过程，在学什么数的时候，你们能想到点什么？

生：学分数的时候。

师：你想到了哪个分数？

生：4/10。

师：是不是它也表示4/10啊？平均分成10份，涂了其中的4份，原来0.4跟4/10表示的意思是一样的（板书：0.4=4/10）。我们再来看橡皮是多少钱？（出示橡皮0.8元）

生：8角。

师：0.8元就是8角钱，8角有没有1元多？假使还让这个长方形表示1元，你能在这个里面表示出0.8元吗？不动笔，把你的想法说出来。

生：把这张纸平均分成10份，取其中的8份涂上阴影。（课件演示验证）

师：这个0.8跟哪个老朋友有联系？

生：8/10（师板书：0.8=8/10）。

师：同学们，假使这里还有一个长方形，用它表示1，你能不能任意地涂上几份，把它用小数表示出来？

学生操作，在练习纸上分一分、涂一涂。

师：谁愿意来展示一下？

生1：我把它平均分成10份，涂其中的1份就是0.1，等于1/10。

生2：我把它平均分成10份，涂其中的3份就是0.3，等于3/10。

生3：我把它平均分成10份，涂其中的7份就是0.7，等于7/10。

师：这样，老师把大家刚才完成的作品作一个整理。电脑演示：依次涂色，屏幕上相应地显示出0.1=1/10，0.2=2/10……0.9=9/10。

师：从这些数据中，你能看出点什么？

生：零点几就表示十分之几。

（接下来教学1.2元，教师给出1.2元的分数面积图形，让学生说出小数，并说一说想法）

片段三：在米尺上进一步丰富学生的理解

师：老师这里有一把尺，叫米尺，量三根彩带的长度。（课件演示两根彩带分别延长到1分米、9分米，学生相应地说出小数）

师：再量第三根彩带，现在有什么办法量出它的长度？（继续延长到13分米）

生1：再拿一根米尺接在后面量。

生2：先在1米的地方作个记号，再把尺子移过去量一量。

（课件演示把多余的部分移到米尺的一端测量，得到1.3米）

师：刚才又有同学想到在后面接上一个尺子，这样就变成了2米尺，可以看出多长——1.3米。

片段四：在数轴上建构小数的意义

师：假使老师的带子更长，2米尺也不够了，再接变成3米尺，3米尺也不够了，怎么办？数学上我们有一种更简单的方式来表示，我们一起看。

师：我画一根带箭头的线，再点上点不就表示出来了吗？

师：这个箭头里还可以有哪些数啊？如果往后再延长一点，就出现几？

生：3。

师：在这条线上出现的0，1，2，3，我们都叫做自然数，也就是整数。把这些数之间平均分成10份，不就产生一些小数了吗？（课件出示）

师：看看这些地方分别代表哪些小数？（0.1，0.5，1.2，1.7，2.3，2.9）

教学赏析：

“认识小数”是苏教版三年级下册第十一单元的内容，虽然学生是第一次学习，但老师为他们提供了一次再创造与发现的过程，学生学得轻松、愉悦，自主地完成了知识的建构。

1.重组教材，把握学习起点。

学生学习小数的数学现实来源于两个方面：一是已有的知识经验，即整数和分数的知识，特别是分母是10的分数意义；二是生活经验，包括学生日常生活接触到商品价格、长度单位等方面的知识。教师充分利用这些有利的条件，调整了学习材料的呈现次序，从学生熟悉的商品价格入手，为学生学习小数搭建了脚手架，降低了学习难度。

2.经历过程，抓住知识本质。

数学家弗赖登塔尔指出：“学习数学的唯一正确方法是实行再创造，也就是由学生本人把要学的东西自己去发现或创造出来，教师的任务是引导和帮助学生进行这种再创造的工作，而不是把现成的知识灌输给学生。”以往很多教师都是通过“米尺”来告诉学生“5/10米还可以写成0.5米”，教师除了采用直接讲解好像别无他法，学生对0.5米的意义很难真正理解。教师把它设计成具体可操作的探索活动，在学生明确了0.4元就是4角后，让学生通过在表示1元的长方形中分一分、涂一涂，表示出0.4元，借助于直观图示的形象支撑，建立起了一位小数的“直观模型”即分数的面积模型，学生初步感知0.4元和4/10元表示的意思是一样的，不留痕迹地沟通了两者之间的联系，也渗透了学生由数思形的意识。教学1.2元时，教师给学生提供了直观图，意在见形思数，数形结合的思想在这儿体现得淋漓尽致，正可谓“数形结合百般好，割裂分家万事休”。

3.多元理解，促进有效建构。

抽象的数学概念概括了大量的具体材料代表的一类数学材料的本质属性，教师要引导学生经历将丰富的材料进行抽象、概括，使感性认识上升到理性认识的过程。教师把学生置于货币单位的背景中，让学生初步理解了小数。在此基础上借助长度单位这个背景将小数与分数的关系进一步地沟通与内化，最后让学生在半抽象半形象的数轴上领悟到十分之几可以写成零点几，零点几表示十分之几。教师悄然无声、水到渠成地帮助学生建构了小数的意义，学生的思维完成了从感性到理性的飞跃。

责任编辑：赵关荣