“数学思维”与“数学思想”的教学
2013-04-29薛文辉
薛文辉
数学思想是指“将具体的数学知识忘掉后剩下的东西”,它形成于学生应用数学知识、方法解决问题的过程中,是对数学知识和基础知识和基本技能的一种本质的认识.《义务教育数学课程标准(2011版)》把数学思想作为“四基”之一,很多教师在讲评数学习题时,只顾基础知识、基本方法、基本技能的讲解而忽视数学最重要的数学思想方法的渗透,这与郑敏信教授在《“数学思想”面面观》中所提倡数学思想方法的教学“不应求全,而应求用”的观点一致.教师在课堂教学中通过学生认识具体的知识内容及解决问题的思维过程“由显及隐”揭示其中蕴含的“数学思想”.下面通过笔者的教学片断,揭示“数学思想”与“数学思维”的教学.
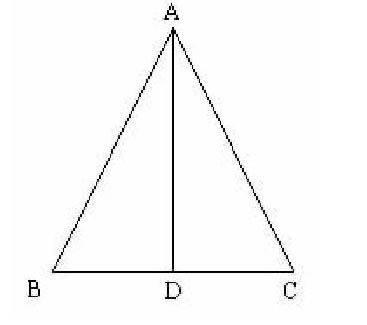
例1:在△ABC中,AB=AC,AD是中线,△ABC的周长为34cm,△ABD的周长为30cm,求AD的长.
师:这条题目没有图形,可以首先画出图形帮助理解.
生1:动手画出如下的图形.
师:你们如何思考这个问题?
生1:34÷2=17,30-17=13.
师追问:你是如何思考的?
生1:由AD是△ABC的中线得BD=CD,又由已知得AB=AC.
由于△ABC的周长为34cm,因此AB+BD=AC+CD=34÷2=17.
又由于△ABD的周长为30cm,因此AD=30-17=13.
师:你是如何想到用这种方法解决这个问题的?
生1:我将△ABD的周长作为整体来考虑,AB+AD的长也整体考虑.
生2:受生1的启发,我也可以这样解决问题.
师:说说你的解决问题的途径.
生2:因为△ABD的周长为30cm,可得△ACD的周长也为30cm,30+30=60就为△ABC的周长再加2个AD的长,所以60-34=26就为两个AD的长,就可以得AD的长为13cm.
生3:将以上两个同学的方法总结一下得到如下解法:由AB=AC,BD=CD,AB+BD=AC+CD=34÷2=17cm,可得AD=△ABD的周长-(AB+BD)=30-17=13cm
师:你总结得非常好!老师接着讲评下一条作业中的问题.
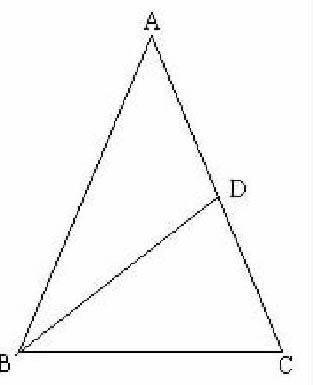
例2:如图,在等腰三角形ABC中,AB=AC,一腰的中线BD将这个等腰三角形的周长分成15和6两部分,求这个三角形的腰长及底边长.
生1:受上面的启发,我是这样思考的:由AB=AC,BD是AC的中线得AD=DC,运用分类讨论的思想方法:当△ABD的周长是15时,则△BCD的周长是6,设AD为1份,则AB为2份,易得AD=DC=5,AB=10,BC=1;当△ABD的周长是6,则△BCD是15,同样的方法可得AD=DC=2,AB=4,BC=13,由于4+4<13,故这样的三角形不存在.
师:你这种解法主要是运用小学算术按比例分配的方法.
生2:我运用方程与分类讨论的思想方法可以解决这个问题,当△ABD的周长是15时,则△BCD的周长是6,设AD=CD=x,则AB=2x,由AB+AD=15,解得x=5,易得AD=DC=5,AB=10,由BC+CD=6,得BC=1;当△ABD的周长是6时,则△BCD是15,用同样的方法可得AD=DC=2,AB=4,BC=13,由于4+4<13,故这样的三角形不存在.
生3:我运用分类讨论的思想方法:当△ABD的周长是15时,则△BCD的周长是6,故AB-BC=15-6=9,AB+AC+BC+BD=21,可得3AB=30,AB=10,BC=1.当△ABD的周长是6,则△BCD是15,得BC-AB=9,AB+AC+BC=21,易得AB=4,BC=13,但考虑到4+4<13,故这种情况不成立.
师:上面三种解决你们最易理解和接受哪种方法?
生:第2种方法.
师:说明方程的解题思想比算术的方法更易让人接受和理解,希望同学们好好体会同,并把它运用到解决数学问题中.再来一题,等腰三角形的两边长是2cm和4cm,则这个等腰三角形的周长为多少?
生1:我利用分类讨论的思想方法:当2cm为腰时,等腰三角形的三边长为2cm、2cm,4cm,则周长为8cm,当4cm为腰时,等腰三角形的三边长为2cm、4cm、4cm,则周长为10cm.
生2:第一种情况不成立,不满足三角形的两边之和大于第三边,故只有第二种情况成立.
师:你说得很好.
师:若改为:等腰三角形的两边长分别为3㎝和4㎝呢?
生3:则两种情况都成立.
老师将题目变一变,有一个内角为30°的等腰三角形,它的另外2个内角的度数分别为多少?你们会解答吗?
生1:我利用分类讨论的思想方法.若30°做顶角,则另外两个内角的度数分别为75°、75°;若30°做底角,则另外两个角的度数是30°、120°.
师:你答得非常好.若改为有一个内角为120°,则另外两个角的度数是多少?
生2:由于三角形的内角和为180°,故120°只能做顶角,另外两个角的度数是30°、30°.
师:你回答得很好!
老师再将题目变一变:有一个外角为45°的等腰三角形,它的三个内角的度数分别为多少?
生1:我运用分数讨论的思想方法,当45°为底角的外角时,这种情况不可能.当45°为顶角的外角时,则顶角是135°,另外两个角的度数是22.5°.
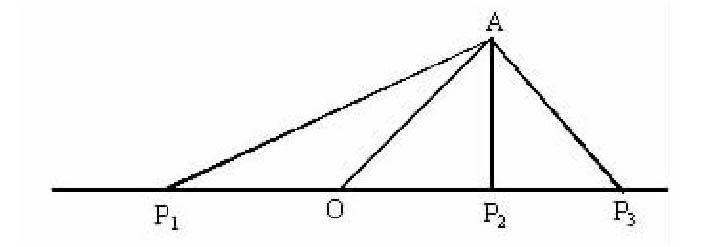
师:你回答得很好.我们再来研究一个问题:在一条直线上,有一点O,线段OA的长为,它与这条直线的夹角为45°,试在这条直线上找一点P,使△APO为等腰三角形,这样的点P共有多少个?
生:我运用分类讨论的思想方法并结合画图可以找到三个点:当OA为腰有2种情况,当OA为底有1种情况.
师:这个问题我们运用分类讨论有及画图的“无字的说明”简单的解法充分体现“数形结合”之“以形助数”的优越性.希望同学们好好体会.
“数学基本思想方法的形成是长期过程,并且是一个潜移默化的过程”,不同认知特点的学生理解上时有迷糊,也有深浅不同的认知,教师对数学思想方法的教学要遵循一个原则,即循序渐进、螺旋上升,并且要善于抓住时机引导、点拨、强化.
