教学之功,先以激趣
2013-04-29包洪梅
包洪梅

赞科夫说:“课本知识如果不经过老师心灵的加工,课本知识传授的越多,您的学生就变得越冷漠,越无知。”生拉硬拽,高谈阔论,假大空式的说教,只能使学生被动的接受知识,实效性不强,难以达到教学要求,尤其是在逻辑性,严密性,抽象性都很强的数学教学中。因此,在实际教学中,教学情境的创设是提高课堂效率的有效手段,也是每个老师追求的目标。
一、激发主体性
例如在学习三角形的中线时,我是这样创设情境的:现在,我校生物小组的同学们获得两种不同的大豆种子,一种是一位同学的亲戚从国外带回来的,一种是同学们网上订购的。他们要比较这两种大豆的产量,而学校只有一块三角形的实验地,他们想把实验地分成面积相等的两个三角形来种植大豆,你能帮他们分吗?
问题提出后,学生们十分感兴趣,纷纷议论,连平时数学成绩较差的学生也跃跃欲试,甚至生活中的办法也来了,学生们学习的主体性很好地被调动了起来,在不知不觉中投入了数学课堂的思维活动之中,把实际问题(三角形的实验地)抽象成数学模型(三角形)后,要解决实际问题,就要充分利用好数学模型,研究与之有关的只是,进而有效地完成本节课的教学目标。
二、激励求知欲
问题是数学的灵魂。教师要善于将所要解决的课题寓于学生实际掌握的知识基础之中,造成心理上的悬念,把问题作为教学过程的出发点,以问题情境激发学生的积极性,让学生在迫切要求引出课题,再引导学生分析问题的实质,并用数学语言概括出这个实质。这样,就由学生自己从问题出发获得了数学知识和结论。
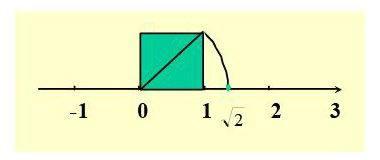
比如说苏科版八年级上册“实数”中介绍了无理数的概念。无理数的概念对于学生而言是非常抽象的,为了让学生感知无理数是客观存在的,课本中设计了这样一个问题:有理数都可以用数轴上的点来表示,反过来,数轴上的点是否都表示有理数呢?能不能在数轴上找到一个点,它表示 呢?
通过引导,学生不难发现在数轴上建立一个边长为1个单位长度的等腰直角三角形,它的斜边的长度就是√2,示意图如下:
通过在数轴上找到 ,让学生真正感受到无理数是客观存在的,而且也可以在数轴上找到其他的无理数。数形结合的思想在这里得到最充分的体现。
三、贯穿实践性
情境教学注重“情感”,又提倡“学以致用”,努力使二者有机地统一起来,在特定的情境中和热烈的情感驱动下进行实际应用,同时还通过实际应用来强化学习成功所带来的快乐。
例如:在教《字母表示数》这一课时,上到引导学生探索规律这一环节时,我让学生亲自动手搭火柴棒,通过相互合作,最后交流得出了四种规律。(如下图所示):
不同的图像就会有不同的规律发现。这样让学生在操作中思维,在思维中操作,理解了字母可以表示任何数或规律。《新课标》也指出有效的数学学习活动不能单纯地依赖模仿与记忆 ,动手实践、自主探索与合作交流是学生学习数学的重要方式。这正象赞可夫所说的:“教学法一旦触及学生的情绪和意志领域,这种教学法就能发挥高度有效的作用。”
实践操作不但使学生获得了定理的猜想,而且受到了证明定理的启发,显示了很大的智力价值。
经过长期的实践证明,好的数学情境能引起学生的问题意识、参与意识和合作意识.使学生在情境中产生好奇、怀疑、困惑、渴求、探究、交流、协作、分享等活动,让学生在“做数学”的实践活动中学习数学,在数学情境中不断产生问题,不断分析和解决问题,从而获得对数学的真正理解。在数学教学中创设数学情境是进一步深化数学课程改革的需要,也是提高教师自身素质的需要,我们将在今后的教学实践中进行根深入的探讨。
