数学问题解决的策略与方法探究
2013-04-29陈建洪
陈建洪


学生的数学学习一般遵循这样的步骤:领会知识→学习技能→积累经验→形成方法和策略→解决数学问题。这是一个呈现为螺旋式上升状态的学习过程。在日常教学中,安排习题作业是培养学生问题解决能力的主要途径。在频繁的解题训练中,学生常常会遇到一些难题,自己无从下手。待教师分析一番后学生很容易理清了思路,于是,教师和学生也就释然了。
但是我们应当进一步反思:为什么学生总是需要教师的引领才能理清自己的思路,找到解决问题的办法?为什么自己很少能够独立获得解决问题的诀窍?这说明我们的数学教学存在着不足:教师总是和盘托出解决问题的思路,却没有将获得思路的策略和方法传授给学生,没有提升学生数学思维的水平。长此以往,学生就总是依赖教师,变得不再思考,不能思考。数学教学也因此呈现出被动、沉闷、低效的状况。
我们到底什么时候才能摒弃授之于鱼的做法,让学生学会自己捕鱼呢?在此,笔者不揣浅陋,将自己的思考和认识简述于下,以期抛砖引玉。
波利亚在《怎样解题》一书中指出,解题的过程分为四个阶段:弄清问题、制定计划、实行计划、回顾。显然,获取解题路径的关键在于前两个阶段。也就是说我们需要从厘清题目中的数学关系入手,进而寻求简捷有效的解题思路。简单地说,这是我们解决数学问题的基本策略。下面就此策略谈谈操作上的一些方法。
一、理解问题,将已知条件和问题了然于胸
如何才能将已知条件和问题了然于胸。通常可以采取以下几种做法:
1.反复阅读。有些问题信息量较多,或者隐藏的条件较多,反复阅读可以帮助我们记住到所有的已知条件,挖掘出其中的隐藏条件。比如下面这个问题:一次象棋比赛共有10名选手参加,他们分别来自甲、乙、丙3个队,每名选手都与其余9名选手各赛一局,每局棋的胜者得1分,负者得0分,平局双方各得0.5分。结果甲队选手平均得4.5分,乙队选手平均得3.6分,丙队选手平均得9分。那么甲、乙、丙3队比赛的选手各有多少人?上述题目中的信息量很大,只有反复阅读,才能把比赛规则、记分方法、各组得分情况熟记下来,并在反复阅读中,感受到“乙队选手平均得3.6分,丙队选手平均得9分”这两个特殊的平均得分,从而找到问题解决的突破口。
2.整理条件。对于文字表述的问题,初读一遍很难做到明了。以表格、摘录条件等方式进行整理,有利于我们明确已知和问题。比如下面这道题目:已知盐水若干克,第一次加入一定量的水后,盐水浓度为3%,第二次又加入同样的水后,盐水浓度为2%,求第三次加入同样的水后盐水的浓度。按照操作的过程进行整理,可以使原来的条件更加条理,利于对比和思考。
3.画图。儿童是借助形象来思考的。文字表述具有间接性,我们在进行数学阅读时,脑中往往是有表象的,准确地借助图形把已知和问题表示出来,有利于我们理解问题。比如数学中的行程问题,分数应用题,和差问题、差倍问题、和倍问题、几何图形问题等都要借助图形帮助自己理解题意。
当然,这里列举的只是理解问题时的几种常用方法。在面对具体的问题时我们也不会孤立的运用某一种方法,而是多项并举。
二、寻求思路,架起已知条件和问题之间的桥梁
明确了问题,我们就会进行思考,我们往往会动员和组织我们的原有的解题经验,试图类推至此,或者对已知条件进行分离和组合,希望从众多的已知条件中找到解决问题的关键条件进行聚焦式的思考,或者将不同的条件进行组合,以期推论出新的条件。有时我们会从已知出发,采取递归模式,逐步靠近问题。有时又会从问题出发,不断分析转化,力图逼近已知条件。当我们在已知条件和问题之间建起了桥梁,我们也就顺利地解决了问题。这个过程是复杂的,不可能寻得解决一切问题的万能解法。但是其间还是有章可循的。在这个寻求思路的过程中,我们通常可以做出以下努力:
1.调动原有的解题经验。面对一个新问题,我们往往会进行辨认,很自然的就会和原先熟悉的情景和问题进行沟通,然后动员和组织原有的知识储备和解题经验,试图用自己掌握的思路去解决它。因此,获得良好的解题思路,必然需要良好的知识储备和丰富的解题经验。什么样的解题经验更利于我们动员和调动?波利亚指出:良好的组织使得所提供的知识更易于用上。信息加工心理学也指出,人脑和计算机一样之所以具备智能,关键在于他贮存了一系列形如“如果/那么”形式编码规则的缘故,即产生式。教师与学生相比,除知识经验的多寡外,更重要的区别在于:教师贮存的是产生式系统,而不是简单的事实;教师的数学知识形成了良好的组织,能够融会贯通,而学生往往难以把握不同知识之间内在的联系。由此可见,良好的解题经验是获取解题思路的基础性条件。
2.一般问题特殊化。叠加模式是解题模式中的一种。运用时通常包括两个步骤:第一,为了求得一般情形的解,先处理一个特殊情形;第二,利用一些指定的代数运算把一些特殊情形组合起来,从而获得一般情形的解。简单的讲就是:一般问题特殊化。例如下面这道题目:如下图1所示,在腰长为10厘米,面积为34平方厘米的等腰三角形底边上任意取一点,设这个点到两腰线段的垂直线段的长分别为a厘米和b厘米,那么a+b的长度之和是多少厘米?因为是底边上上任意一点,学生往往感觉无法捉摸。教师在教学时不妨故意降低要求:“你觉得这一点点在什么地方你会解决,你就把点点在哪里。”学生通常会把点点在底角顶点(如下图2)或者是底边中点(如下图3)。(1)点在底角顶点,学生很容易求出a的长度:34×2÷10=6.8厘米,a+b=6.8+0=6.8厘米;(2)点在底边中点。可以连接等腰三角形的顶点和底边中点。分别求出a和b的长度:34÷2=17厘米,17×2÷10=3.4厘米,3.4+3.4=6.8厘米。(3)一般属于特殊,有了上述两个特殊情况的解法,学生就很容易猜测出一般情况下,a+b=6.8。同时也会受图3的启发,连接图1中等腰三角形的顶点和底边上的哪一个任意点。进而列出10a÷2+10b÷2=34,进而推出5a+5b=34,a+b=34÷5=6.8。
3.合情推理。解题思路的获得并不是纯逻辑的。离不开尝试、猜想、验证、归纳等不完全可靠的方法。这个过程需要解题者具有较好的元认知能力:时刻明确目标在哪里?自己在哪里?自己选择的路径是否可靠?同时也需要,解题者具有较好的调整能力。遇到困难时,能够及时调整方向,能够从自己的错误中寻求有益成分,而不是全盘否定。从而才能在不断的尝试、调整、验证中获得思路。比如算式迷题、数阵问题中就存在着大量这样的问题。以下面这个问题为例,我们来看一看合情推理中的思维活动:将1—8分别填入下图1中的四个圆以及相互交叉所形成的区域内,使每个圆内的三个数字之和相等,并且使这个和尽可能地小。
读完题目,我们并不是一下子想到完美的思路。探究过程通常会经历下面的两个阶段:
1.调动经验进行尝试。由于8个空格分为两类:交叉处和外围。因此我们把1-8分成两组,四个数填在交叉处,四个数填在外围。由于和尽可能小,先选择4个较小的数1、2、3、4填在交叉处(如上图2、图3),四个较大的数在外围进行尝试,但是无论如何也不能使四个圈内3个数的和都相等。2、反思失败原因调整思路;失败后,恰是寻找思路的关键点。错误并非完全没有价值,其中往往蕴含着通往正确思路的有益成分。值得关注的是,大多数学生往往采取全盘否定,而不是寻找错误的原因,从错误走向成功。仔细分析错误的过程,我们会发现:中间四个数,有大小搭配和依次排列两类填法(如上图2、图3所示)。第一类,1+4=2+3,找不到相同的数来搭配。第二类,圆内已知两个数的和分别是3、4、6、7,没有连续性。而剩下的四个数5、6、7、8却是连续的,因此无法搭配成功,只能使四个圈内的和分别是:11、11、12、12。从第二种错误中,我们能够得出四个圈的总和是46,不是4的倍数。由此联想到,要想填出正确的结果,就要增加四个圈的总和,也就是让中间四个数的和增加2,改为1、2、3、6。然后再进行尝试。很容易得到正确的填法(如上图4所示)。探究思路的过程并不全是逻辑,离不开经验的运用,反思和调整,以及灵感般的顿悟。而学生最不擅长的在于反思和调整,他们往往在失败后往往是全盘否定原来的想法,再一次回到起点沿着另一条路走下去,思路也因此与他们失之交臂。
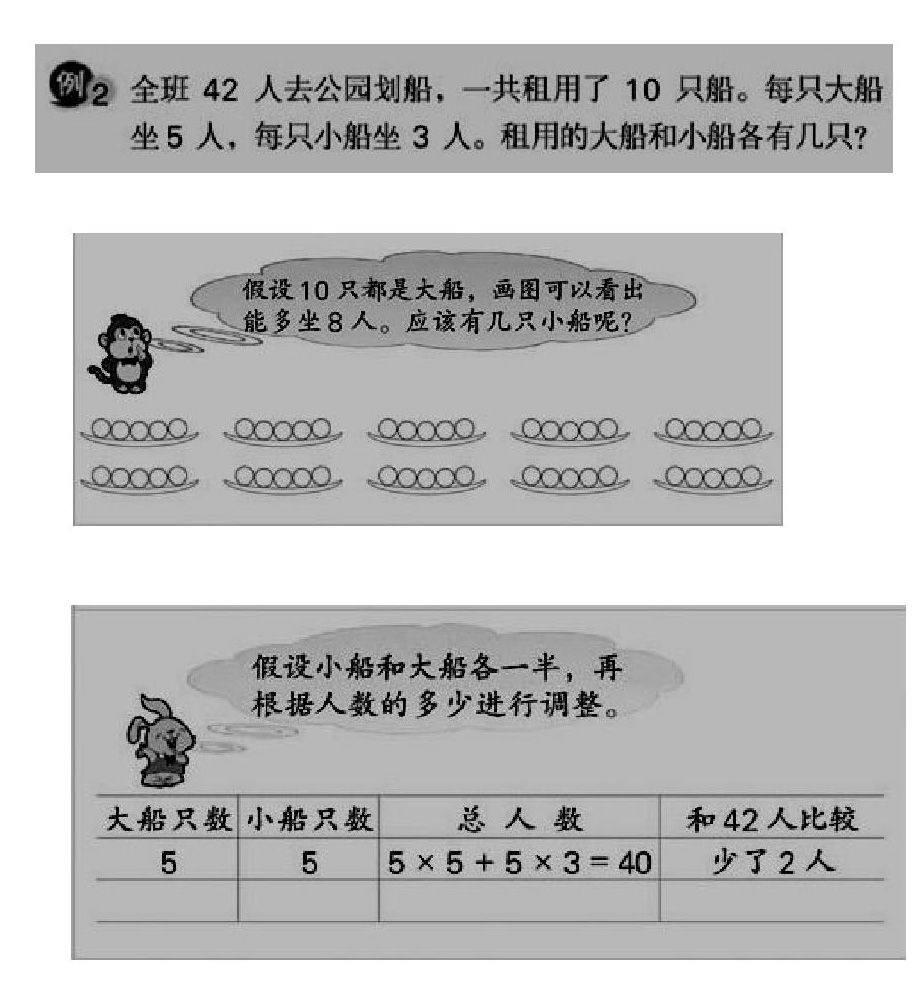
2.从笨方法入手。很多时候好的思路是从所谓的笨方法中发现出来的。如教材编排解决问题的策略时,一一列举的策略、画图策略和假设策略分别安排四年级下册、五年级的上册和六年级的上册。实际上也存在着笨方法和巧妙思路的关系。比如,六年级上册用假设法解决问题的例题如下:
教材就是先利用画图策略和一一列举的策略,来帮助学生提炼假设策略的。
画图和一一列举对学生来说是笨方法,但是学生在一一列举的过程中,能够体会到将一只小船调整成一只大船就可以多坐2人(反之少坐2人)。理解了这一点,也就很容易理解假设法的思路:比如假设租的10条船全是小船,一共可以坐10×3=30人,比总数42人少了42-30=12人,一只小船调整成一只大船就可以多坐2人,因此一共要租12÷2=6只大船,10-6=4只小船。使用笨方法的过程,是在获取感性经验,感性经验充分了,自然会升华、抽象,不止步于笨方法,对笨方法进行反思,巧妙的方法也就出来了。因此,我们要正确的看待笨方法,一味的找快捷方式往往会没有出路的,多画图、多尝试、多列举,从已有的笨方法出发,巧妙思路才会不期而至。
