初中数学学习中的反思
2013-04-29胡昌林
胡昌林
摘 要:数学反思性学习是学生以自己的学习活动为思考对象,主动对自己的学习行为、决策以及由此产生的结果进行审视和调控,是学生提高自我知识水平、促进学习能力的发展并使自己的学习活动顺利进行的有效途径。
关键词:初中数学 ;反思;目的意义;主要内容;学习方法
一、数学学习中反思的目的和意义
建构主义学习观认为:“一切知识最终都必须通过主体的建构活动才能得以完成,反思是建构主义的一个核心特征。关注学生学习中的反思,可以促进学生自主学习能力的提高。”因此要教会学生学习,就必须让其学会反思,带着反思性学习的思维参与到学习中去。反思性学习是一种心理活动,是一种认识论的方法和思维活动的过程。具有很强的自主性。反思性学习不仅仅是对学习一般性的回顾或重复,而是学生对自己的学习方式、认知方式、理解程度、思维过程等方面在次自我认识、自我评价,以及对自己学习进行度、学习心理的自我监控的再次审视,是学生主体意识发展的完美体现。
数学反思性学习是学生以自己的学习活动为思考对象,主动对自己的学习行为、决策以及由此产生的结果进行审视和调控,是学生提高自我知识水平、促进学习能力的发展并使自己的学习活动顺利进行的有效途径。因此培养学生经常性的进行自我诊断和反思,可以让学生感受和理解知识产生和发展及应用过程,也是提高学生学习效率,促进学生知识的建构,使学生的创新能力和思维能力得到进一步提高。
二、数学学习中值得反思的主要内容
数学思维活动有三个要素:对象、过程和结果。因此数学学习反思也可以相应地分为对数学思维活动的对象、过程和结果的反思。对数学活动对象的反思包括“对数学问题的特征、涉及的数学知识、思想方法进行反思;对数学命题、语言及思维活动有联系的问题的反思”;对数学活动过程的反思包括“对思考、理解、推理和解决问题的过程的反思”;对数学思维活动结果的反思包括“对解题思路、语言表达以及对数学结论进行反思”。
若从数学学习反思问题的性质看,数学学习反思的内容又可分为:(1)经验性反思,着重反思问题涉及了解哪些知识、技能、技巧和数学思想方法;(2)概括性反思,指在对同一类数学问题的解决方法进行优化、概括、形成一种清晰的解题思路,上升为一种数学思想方法;(3)创造性反思,指对数学问题的重新认识,以及扩大、引申和探究;(4)错误性反思,对解决问题过程中的错误进行纠正的思考,找到产生错误的根源,进而调整自己的认知结构,防止以后出现类似的失误。
三、培养学生数学学习反思的方法
(一)创设情景,激发动机
反思过程是情感与认识密切相关并互相作用的过程,它不仅需要智力加工,而且需要有情感因素的支持。因而有无反思的动机非常重要。在数学教学中,教师要着力通过实验操作、设疑置难、创设情景等方式,营造一个促使学生反思的学习氛围,以激发学生的反思动机。
例如教学“三角形三边关系”时,我让学生用下列各组的三条线段分别去摆三角形(每条线段用小木棒代替):(1)3cm,4cm,5cm;(2)6cm,8cm,12cm;(3)7cm,6cm,6cm;(4)5cm,6cm,11cm;(5)5cm,6cm,12cm ;对(1)(2)(3)组,学生能很快摆出三角形,而对于(4)组合(5)组,学生无论如何摆不出一个三角形。这就引导学生进行思考“什么样的三条线段才能组成一个三角形?一个三角形的三边究竟有什么规律?”学生在求知欲的驱使下,会自觉地进行反思,得出一个三角形三边关系的规律。
(二)反思策略,注重方法
在平时的学习过程中,学生总是根据问题的具体情景来解决问题方法,这种方法总受到问题情景的制约,如果不加以提炼和概括,那么它的适用范围就很有限,不利于知识的迁移。因此教师在教学设计时要留给学生反思的问题;在课堂教学中给学生留下反思的时间和空间;在解决问题后让学生反思解题过程,分析具体方法中包含的数学基本原理,对具体方法进行再加工,引导学生在思维策略上回顾总结,从中提炼出让学生认可的数学思想方法,达到举一反三的目的。例如学生解决了“四边形内角和等于360度以后,我们可以设置这样的问题:四边形的内角和是如何探求的(转化为三角形)?,那么五边形的内角和你会探求吗?六边形、七边形------n边形的内角和是多少?”
(三)创设反思,思练结合
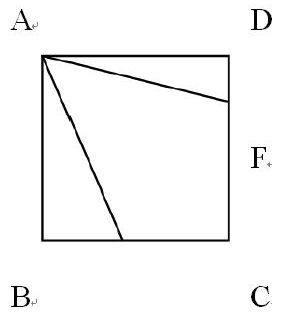
一道典型例题解完以后,教师应充分发挥典型例题在知识与能力层面的辐射功能,从原题中挖取出与原题有关,且让学生从更深的层面了解题目,提高学生思维深刻性的问题,让学生思维开阔起来。例如如图(1),正方形ABCD中,E、F分别是BC、DC上两个动点,∠EAF=45°通过证明可知BE+DF=EF.原题的解决本来可以到此为止。但实际上就这题还能作一番文章,引导学生就以下两个方面进一步探索:
(1)若BE+DF=EF,则∠EAF的度数是45°吗?题设与结论互换,培养学生逆向思维的能力。
(2)若E,F分别是从B,C同时出发,而且BE+DF=EF,当E在BC中点时,F会落在CD中点吗?学生一般会认为E在B时,F在C,E在C时,F在D,那么E在BC中点时,F也会在CD中点,其实不然。
因此,两动点不会同时出现在边的中点处。这个反思练习让学生的学习热情再次高涨,探究欲望再次飞扬,思维水平进一步提高。
(三)反思方法,优化过程
在数学教学过程中,我们经常发现有许多学生学习很刻苦,也做了许多的题目但对自己的解题方法的优劣却从不加评价,作业中常常出现过程单一、思路狭窄、逻辑混乱、主次不分等现象,产生这一现象的主要原因是学生思维过程缺乏灵活性。因此在解题过程中,教师应引导学生对解题思路与方法进行反思,正确评估自己的解题方法,优化解题过程,领悟数学解题的通性通法。例如某校有20位教师报名参加乒乓球单打比赛,比赛采用淘汰制。请问:这次比赛要打多少场球才能结束?在解这个题时,几乎所有的学生都按常规思考方法解决本题。但解完题后教师问:如有1万人参加比赛应打多少场才能结束,学生便束手无策。这时,教师应启发学生反思、评估自己的解题方法,说明这不是解决问题的最佳方法,进而引导学生换一个角度分析此题,用逆向思维的方法处理,由于是淘汰制,因此比赛一场便淘汰一人,淘汰的人数是比赛的场数,如有n人参加比赛,共需比赛(n-1)场。
