浅谈小学生函数思想的培养

郑前清

【摘要】在小学数学教学中，有效渗透数学思想方法教育，可以帮助学生更好地理解和掌握数学知识，形成良好的思维品质。而函数思想是诸多数学重要思想方法之一，适时、有效渗透于相关知识的教学中，为学生的后续学习和发展奠基。

【关键词】数学教学；函数思想；渗透

数学思想方法是数学的精髓。《数学课程标准》（2011年版）明确提出 “通过义务阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验”的总目标，给数学教学指明了方向，要求我们要不失时机地向学生渗透一些基本的数学思想方法，指导学生运用数学思想方法科学地思考解决问题，从而促进学生数学素质的提高。

函数思想是诸多重要数学思想方法之—。小学数学内容的知识体系是培养小学生早期函数思想的极好载体。结合有关知识的教学渗透函数思想，让学生初步感受事物间的不断变化与联系，有助于训练学生的思维品质，加深学生对知识的理解和掌握，初步培养学生利用函数思想分析、解决问题的能力。

小学数学教材可从以下几个方面对函数思想加以渗透：

一、抓住变量思想的引入。

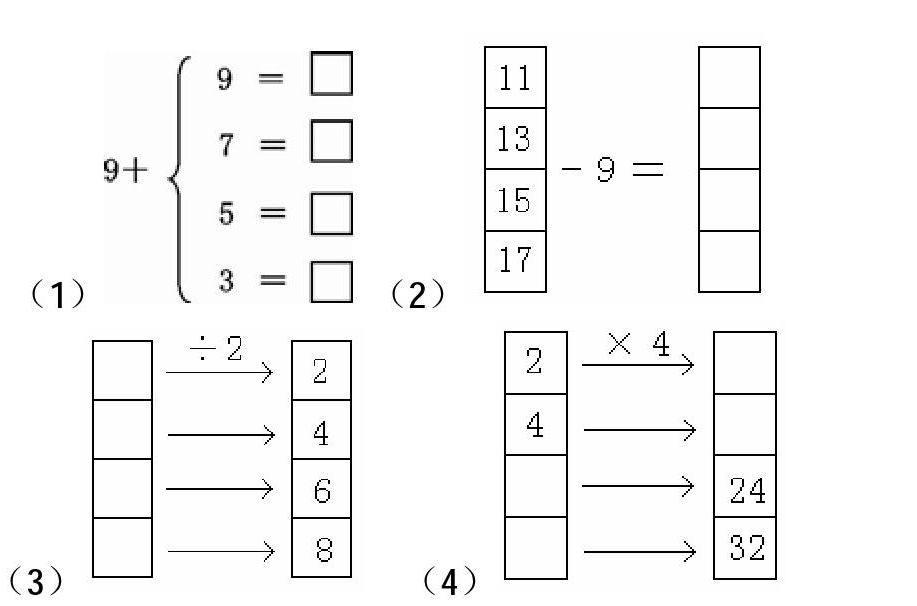
在苏教版小学数学一、二年级教材中有如下形式的一些练习题：

这种形式的练习一方面弥补了加、减、乘、除运算题型的单调与不足，更重要的是为了引入变量思想。其实质是给出了两个集合及其元素间的对应法则，根据对应法则，找出一些元素的对应元素。通过这种题型的练习，可使学生初步认识到：两个变量之间，当一个确定后，另一个随着确定（按照某种法则），一个量变化时，另一个量也跟着变化（按照某种法则），两个量之间的变化是相关联的。初步培养学生用变化、联系的观点看问题。

二、抓住用字母表示数的教学。

用字母表示数是从算术过渡到代数的转折点。没有用字母表示数这一基础，在某一过程中可以取不同数值的量就无法加以表示，变量之间的相互依存、相互制约的数量关系就难以得到完美的表述。从这一意义上来说，用字母表示数是函数的基础。

用字母表示数渗透函数思想主要表现在以下两个方面：

1.对于整数四则运算性质及变化规律和分数的基本性质，除了用文字加以叙述外，还辅之以字母表示。

如苏教版小学数学四年级下册第106页例题：

摆1个三角形用3根小棒；

摆2个三角形用小棒的根数是：2×3；

摆3个三角形用小棒的根数是：3×3；

……

摆a个三角形用小棒的根数是：3a；学生通过摆三角形，发现小棒的根数随着三角形个数的增加（减少）而增加（减少），但二者之间的关系是不变的。再如商不变的规律a÷b=（a×m）÷（b×m），a÷b=（a÷m）÷（b÷m）（b≠0，m≠0）；利用字母表达式进行分析：a、b确定后，商的值就确定了。当m “变”时，被除数和除数的值在变，但商的值不变。引导学生用变动的观点分析问题，可加深学生对规律的掌握和性质的理解，同时也为后续的学习做了很好的孕伏。

2.用字母表示几何图形的周长、面积、体积公式。

如：正方形周长C=4a，正方形面积S=a2。学生通过应用公式，对不同边长的正方形周长、面积的计算，会逐步认识到：正方形的边长确定后，周长、面积也随之确定。正方形的边长变化时，周长、面积也随之变化，且周长、面积的变化与边长的大小是相关联的。进一步培养了学生用运动、变化、联系的眼光看问题的观点。

三、抓住正反比例概念的教学。

正反比例关系式是引入函数概念的一个极好例子。下面以苏教版小学数学六年级下册正比例概念的教学为例来说函数思想的渗透。

建立正比例概念时，教材中举了两例。

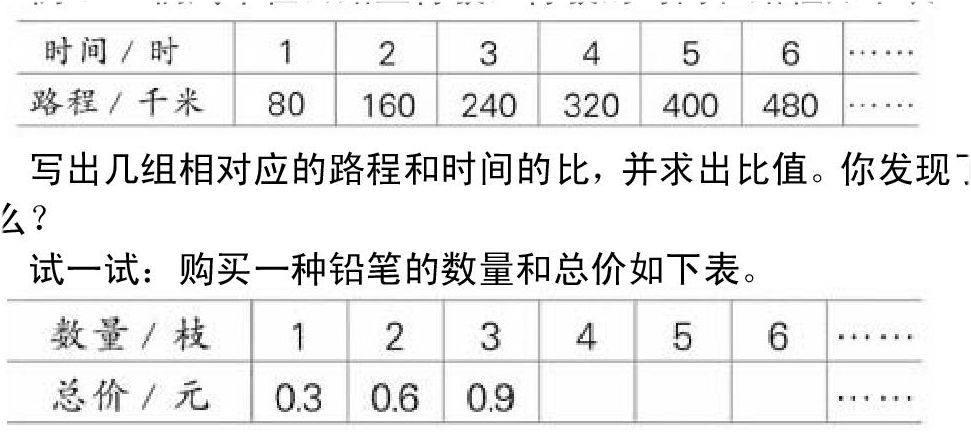
例1 一辆汽车在公路上行驶，行驶的时间和路程如下表。

写出几组相对应的路程和时间的比，并求出比值。你发现了什么？

试一试：购买一种铅笔的数量和总价如下表。

（1）填写上表，说说总价是随着哪个量的变化而变化的。

（2）写出几组相对应的总价和数量的比，并比较比值的大小。

（3）这个比值表示什么？你能用式子表示它与总价和数量之间的关系吗？

教材中采用列表法给出了两个变量（时间与路程、总价与数量）的若干组对应值。利用对应值表，结合概念的建立过程可以从以下三个方面进行渗透：

1.从每一组对应值看，时间（数量）确定后，路程（总价）就随着确定了。即两个变量中的一个量随着另一个量的确定而确定，培养学生按照一定的法则进行量与量对应的思想。

2.从各组对应值整体分析。时间（数量）扩大，路程（总价）也扩大，时间（数量）缩小，路程（总价）也缩小。即路程（总价）随时间（数量）（按照一定规律）的变化而变化。培养学生用运动、变化、联系观点看问题的思维习惯。

3.引导学生观察分析，总结变化规律：路程和时间（总价与数量）的比值是一定的。在文字说明的基础上给出关系式： =速度（一定）， =单价（一定）。用字母表示，抽象为 =k（一定）。最后给出成正比例关系的概念。在分析过程中，要始终抓住“两个量是相关联的”、“比值一定”这些关键词。使学生逐步明确：在相对应的两个量的变化过程中，这两个变量之间是相互依存、相互制约的关系。

函数思想的核心之处正在于它是用运动、变化的观点去反映客观事物数量间的相互联系和内在规律的。学生对函数概念的理解需要一个过程。而在小学数学教学中，我们教学以上内容时，要做到心中有函数思想，注意渗透函数思想，帮助学生形成初步的函数概念，为他们今后的数学学习和发展奠定良好的基础。

参考文献：

[1]《全日制义务教育数学课程标准》（2011版）

[2]义务教育课程标准实验教科书《数学》江苏教育出版社 2007.6 2007.12

[3]《中外著名数学家资料集》编者 胡应华 2008.4

基金项目：省级课题：“小学数学教学渗透数学思想方法教育的有效策略研究”课题批准号：JG11126。