重视发展思维能力，促进数学有效教学

何文娟

数学是思维的体操，是思考的学问。而思维是数学有效教学的核心。在中学数学教学中，怎样提高学生的思维能力？

一、大胆猜想，自由探索

数学猜想是一种创造性的数学思维活动，是培养学生创新能力的重要途径。在教学过程中让学生大胆猜测、假设，提出一些预见性的想法，设想对事物的瞬间顿悟，有利于学生创造性思维的发展。

比如完全平方公式（a+b）2的学习，先引导学生猜想，在错误的猜想结果a2+b2的基础上引导大家计算得出最后的公式（a+b）2=a2+2ab+b2。虽然猜想错了，但学生兴致很高，并进一步猜想（a+b）3=a3+3ab+b3，这时学生没有盲目相信自己的猜想，而是进一步验证出最后的结论： （a+b）2=a3+3a2b+3ab2+b3。虽然前面的两次猜想错了，但大家能更理智地通过它们的特点进一步猜想 （a+b）n，从系数、项数、字母的指数等方面展开了猜想的翅膀，最难的就是系数的规律，个别积极思考的学生把（a+b）n的指数n为1、2、3、4时的展开式的系数列成了表

1

11

121

1331

14641

我兴奋地告诉学生他们发现了我国古代数学家发现的重要规律——杨辉三角，真的了不起，这是大家乐于思考、善于猜想的结果。

二、鼓励求异，大胆求知

求异思维是主体面临问题时，能从多角度、多方位思考问题，使思路由一条扩展到多条，由一个方向转移到多方向的思维方式。求异思维与创新能力有着直接的关系，是创新思维的核心。数学课上教师应多设计一些活动空间，引导学生打破常规思维的束缚，凭借自己的智慧和能力积极地从不同途径、不同角度去思考问题，为学生提供创造空间，提供创造机会，培养创造能力。

例如三角形角平分线性质定理：如图，AD为△ABC内角平分线，求证：=。

很多教师在碰到这类题目时，只是机械地要求学生记牢、会运用这个结论就可以了。但我认为这道题目的证明过程实质是众多知识的运用和反映，应花大力加以证明和引导，要求学生尽可能多地运用各种方法证明。多数学生会考虑构造相似三角形的基本图形——“八字型”“塔型”。

三、变式训练，激活思维

任何一个数学问题的解答思维过程，一般地都可以把它分解为三个基本部分：问题的条件部分、问题的解答过程、问题的结论部分。如果把这三个部分作为变化的因素，可以构成条件变式题、结论变式题、过程变式题。在进行变式题设计时，应主要依据教材的例题与习题。

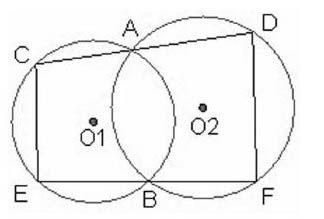
例如，“圆内接四边形”一节的例题是：⊙O1与⊙O2都经过A、B两点，经过A点的直线CD交⊙O1于点C，与⊙O2交于点D，经过点B的直线EF与⊙O1交于点E，⊙O2交于点F，求证：CE∥DF.在此题基础上，可得条件变式题：①已知CD∥EF，求证四边形CEFD是平形四边形；②已知CD∥EF，求证CD=EF.经过如此分析，对培养学生识图、证明的能力是有益的，并且起到了巩固“双基”的作用。

在变式教学中应该强调变式题的设计与训练。遵循学生的认识规律和年龄特征，按照由低到高，由浅入深的原则，设计阶梯度清晰的各类变式题组，加强对学生的训练；注重精讲多练（变式训练），充分发挥教师的主导作用，学生的主体作用和训练的主线作用。在实施变式教学方法的同时，应注意针对不同的内容，不同的教学阶段使用不同的教学方法。如复习课教学，就可以采用“定向—自学—点拨—自测—评讲—自结”程序的方法，对培养学生能力，实现教学目标，提高课堂效益会起到理想的教学效益。

四、开放教学，发散思维

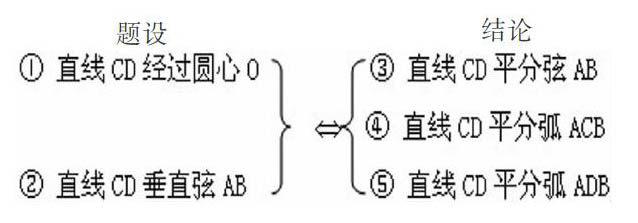
课本在许多地方给我们安排了绝佳的开放问题的内容，例如：垂径定理用其推论的内容绕口且不易分辨清楚，如果将题设的结论用下列方式理顺并由此展开开放式讨论，学生的掌握情况要好得多。如果把题设和结论中的5个条件适当互换，又会如何？

让学生作为主体，讨论这个开放式问题，不难得到：对于一个圆和一条直线来说，如果以上5个元素中的任何两个作为题设成立，则其它3个作为结论也成立。这样可得到垂径定理的9个推论。

此外，还有圆心角、弧、弦、弦心距的关系定理、弦切角定理的证明等。把它们当开放问题处理都能取得很好的教学效果。

责任编辑 罗峰