以“辩”提升学生的数学思维能力

严世林

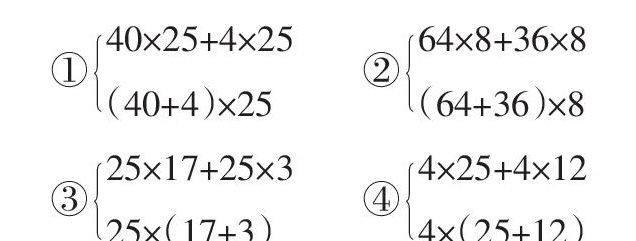
【关键词】辩论 数学课堂 思维能力

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2013）09A-0082-01

课堂上学生之间不同观点、不同方法之间的碰撞，都会激发出耀眼的火花。教师要有意识地诱发、引导这种生生之间的辩论，以此把握教学生成过程中的平衡，创造性地组织教学的实践过程，让学生的数学能力和数学思维在“辩”中得到提升。

一、越辩越深

学生受到心理年龄特点的制约，常常满足于答案的获得，而不愿静下心来细细思索其“所以然”，也不能仔细倾听教师的讲述。因此，教师要精心设计某个知识的“第二生长点”，激起学生继续探究的兴趣，引发他们对已有结论的进一步思考，让学生在思维的撞击中完善知识的构建。

例如，苏教版六年级数学下册《圆柱的体积》一课，有这样一道习题：一个长方形的纸片长6分米，宽4分米。用它分别围成两个圆柱体，A是用4分米做底，6分米做高；B是用6分米做底，4分米做高。A、B的体积大小一样吗？

学生有的认为A的体积大一些，有的认为B的大一些，还有一小部分学生认为两者一样大。教师及时提出一个提议：“既然这样，我们就展开一场辩论赛，看谁的依据最充分。”让学生通过计算巩固圆柱的体积计算公式，培养他们耐心细致的计算习惯和严谨认真的学习态度。

再如教学“线段”这一内容时，我抛出一个问题：“经过两点可以画几条线段？”学生很轻松地就给出答案；我再延伸：“若在这条线段上再加一点，又有几条不同的线段呢？”……接着让学生辩论“点的个数与线段的条数之间有关系吗？”在层层深入中，学生时刻保持着主动探究的积极心态，思维不断得以延伸。

二、越辩越活

“动起来、更精彩！”当学生各执一词、相持不下时，教师不应充当一锤定音的“法官”，也不是吹响终场哨音的裁判，而应针对学生辩论中的焦点，组织学生进行验证，在实践操作中进行自我肯定或自我纠正，不但让知识真正扎根于学生思维的深处，也渗透了实践出真知的科学态度。

例如，在教学苏教版五年级数学下册《圆的面积》一课时，我给学生讲了一个数学故事：阿凡提为达拉老爷解决了一个难题，达拉老爷决定奖励阿凡提，于是他掏出一根绳子对阿凡提说：“聪明的阿凡提，去用这根绳子圈出一块土地吧，圈出的土地就是我对你的奖赏！”同学们，如果你是阿凡提，你会怎么圈呢？

有的学生说圈成一个圆（因为刚刚学过圆的面积），有的学生认为圈成一个正方形，而有的则认为也许应该圈成一个长方形。当他们决定用事实说话时，却又不知道从何入手。這时我让学生取出小绳子，引导他们展开实践活动：

用这根绳子在钉子板上围成不同的形状，想一想，这些图形什么是相同的？

根据不同图形的面积计算公式，你认为绳子的长度为多少更方便我们计算？

算一算，不同的图形它们的面积分别是多少？（可以合理地运用估算）

通过实践的验证，学生不但获得了正确的结论，在操作过程中还体会到了假设法、估算法的灵活运用。

三、越辩越清

在比较中体验，让学生逐步把握住知识的本质核心，发展其实际运用能力。在课堂上就知识的模糊处、易混淆处展开辩论，帮助学生认识知识的运用价值，完整知识结构的整体构建。在学生已有的知识、经验不能对新知进行正确反思时，教师可以适时介入，展开师生之间的辩论，体现教师的主导作用，促使学生的认识越加准确、清晰。

例如，苏教版四年级数学下册《乘法分配律》一课，我设计了这样一组对比练习：

①40×25+4×25

（40+4）×25 ②64×8+36×8

（64+36）×8

③25×17+25×3

25×（17+3） ④4×25+4×12

4×（25+12）

学生们几乎都选择每组中的下一道题来计算，前三组题都体现了乘法分配律的简算价值，学生巩固了“使用乘法分配律可以使计算简便”的切身体验。然而，最后一组题中，由于思维的惯性，绝大多数学生依然选择了4×（25+12）。在教师期待的目光中，学生开始了重新思考，他们中的一部分发现原来4×25+4×12计算起来反而简便一些。教师故作困惑地说：“可是，老师告诉我们，‘使用乘法分配律可以使计算简便呀！”这样引导学生展开辩论，从而帮助学生理解乘法分配律的正确使用，让学生体会到简算的第一步应当仔细观察算式中数字的特点，再决定采取恰当的运算律进行简算。

“辩”的精彩，是因为它符合学生的心理特点，允许和鼓励学生发表自己的独到见解，并在证明、论证的过程中品尝成功的喜悦。教师适时、适当的引领，让学生的思维和能力在充满热情、紧张激烈的辩论得到充分发展和全面提升。

（责编 林 剑）