Improved fixed pointmethod for image restoration

YAN Xue-fei，XU Ting-fa，BAITing-zhu

（Key Laboratory of Photoelectric Imaging Technology and System of the Ministry of Education，College of Optical Engineering，Beijing Institute of Technology，Beijing 100081，China）

*Corrponding author，E-mail：xutingfa@163.com

Improved fixed pointmethod for image restoration

YAN Xue-fei，XU Ting-fa*，BAITing-zhu

（Key Laboratory of Photoelectric Imaging Technology and System of the Ministry of Education，College of Optical Engineering，Beijing Institute of Technology，Beijing 100081，China）

*Corrponding author，E-mail：xutingfa@163.com

We analyze the fixed pointmethod with Tikhonov regularization under the periodic boundary conditions，and propose a changable regularization parametermethod.Firstly，we choose a bigger one to restrain the noise in the reconstructed image，and get a convergent result tomodify the initial gradient.Secondly，we choose a smaller one to increase the details in the image.Experimental results show that compared with other popular algorithms which solve the L1norm regularization function and Total Variation（TV）regularization function，the improved fixed pointmethod performs favorably in solving the problem of themotion degradation and Gaussian degradation.

image restoration;periodic boundary condition;Tikhonov regularization;change regularization parameter

1 Introduction

In modern society，images are importantmedia for human to obtain the information.However，the images are destroyed inevitably during imaging，copying，and transmission，such as image information is polluted by the noise.While，the highquality images are necessary in many areas.So the image restoration is a very important task.It is one of the earliest and most classical nonlinear inverse problems in imaging processing，dating back to the 1960′s.

2 Image degradation model

In this class of problems，the image blurring ismodeled as：

Where f（f∈RAB×1）is a AB×1 vector and represents the unknown A×B original image.g（g∈RAB×1）is a AB×1 vector and represents the A×B noisy blurred image.n（n∈RAB×1）is a AB×1 vector and represents thewhite Gaussian noise.H（H∈RAB×AB）represents the blur operator.In the case of spatially invariant blurs，it is thematrix representation of the convolution operation.The structure of H depends on the choice of boundary conditions，that is，the underlying assumptions on the image outside the field of view.

We consider the original image：

Zero boundary condition means that all pixels outside the borders are assumed to be zero，which can be pictured as embedding the image f in a large image：

In this case，H is a Block Toeplitz with Toeplitz Blocks（BTTB）matrix.

Periodic boundary condition means that the image repeats itself in all directions，which can be pictured as a large image embedded with image f：

In this case，H is a Block Circulant with Circulant Blocks（BCCB）matrix.

Reflexive（Neumann）boundary condition means that the scene outside the boundaries is amirror image of the scene inside the image boundaries，which can be pictured as a large image embedded with image f：

In this case，H is the sum of BTTB，Block Toeplitz with Hankel Blocks（BTHB），Block Hankel with Toeplitz Blocks（BHTB）and Block Hankelwith HankelBlocks（BHHB）matrices［1］.

In this paperwe propose an improved fixed point method with Tikhonov regularization that we claim performs better than other popular algorithms in both subjective and objective judgements of the image restoration ability.It changes regularization parameters from bigger ones to small ones with iterations，and modifies the initial gradient at every iteration to increase the details in the reconstructed image.

3 Tikhonov regularization function

Aswe all know，H is often singular or very ill-conditioned.So the problem of estimating f from g is an Ill-posed Linear Inverse Problem（ILIP）.A classical approach to ILIP is the Tikhonov regularization which can be expressed as：

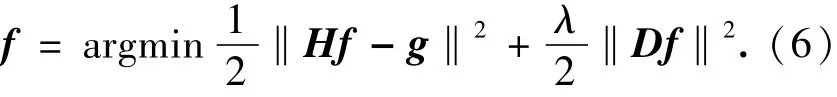
whereλ（λ＞0）is the regularization parameter，D is the penalty matrix.‖Df‖2is the regularizer or regularization functional，which has many choices such as：L1norm regularization functional［2-6］，Total-Variation（TV）regularization functional［7-10］. There are algorithms for solving L1norm regularization functional such as：Gradient Projection for Space Resonstruction（GPSR）algorithm［11］，which includes GPSR-basic algorithm，GPSR-bb algorithm and SpaRSA-monotone algorithm［12］.There are algorithms for solving TV regularization functional such as：Tw IST algorithm［13-14］，SALSA algorithm［15-16］，FTVd algorithm［17-20］and fixed pointmethod［23］.

The fixed pointmethod can be expressed as：

Begin the fixed point iterations：

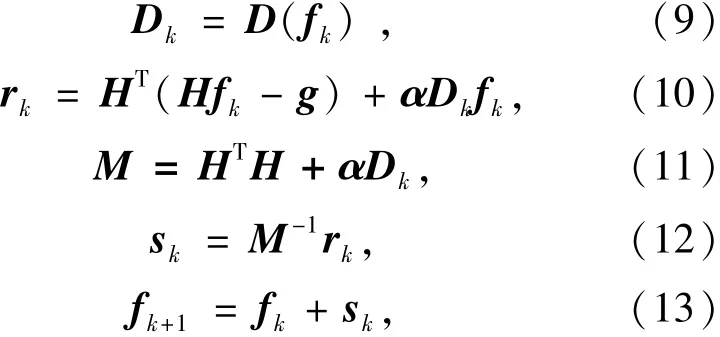
Generally，when rk＜0.001，we stop the iterations.

4 Improved fixed pointmethod

When the boundary condition of image blurring is the periodic boundary condition，we can choose penalty matrix as the negative Laplacian with periodic boundary condition L，which is a B×B partitioned matrix：

where I is an A×A identitymatrix，Θis a A×A zeromatrix.

We use thematlab function psf=fspecial（′motion′，71，56）to create the motion blurring kernel point spread function，and use g=imfilter（f，psf，′conv′，′same′，′circular′）to get the motion blurred image;g=imnoise（g，′Gaussian′，0，1×10-3）to add white Gaussian noise of zeromean and standard deviation 1×10-3.We run the fixed pointmethod and compare the reconstructed imageswhenλis different.

In the Fig.1，there are 256 pixel×256 pixel original image Lena（a），motion blurring kernel noisy blurred image（b），and image reconstructed when λ=10（c），λ=1（d），λ=10-1（e），λ=10-2（f）.

We can find that when we choose a biggerλ，restored image has less noise and also less details; however，when we choose a smallerλ，reconstructed image has more noise and also more details. Therefore，we propose the change regularization pa-rametermethod.Firstly，we choose a biggerλto restrain the noise in the reconstructed image.Running the fixed pointmethod to get the convergent result f，and convolving with H tomodify the initial gradient r0to the real value.We use the new f，r0as the initial ones to run the fixed pointmethod again.Secondly，we choose a smallerλto increase the details in the reconstructed image.Repeating the above process until the suitable value is found：

Fig.1 Image restoration comparison of different regularization parameters

1.Give the initial value：λ=λ0，k＜1，f0=0，r0=-HTg;

2.Run the fixed pointmethod to get the convergent result f;

3.f0=f，λ=λ·k，r0=Af0-HTg，back to 2.

4 Experimental results

Simulations are carried out to test the proposed algorithm.The Mean Structural Similarity Index Method（MSSIM）［24］is selected to evaluate the restored image quality.The SSIM index is defined as follows：

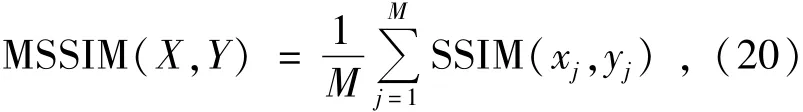
Where xjand yjare the image contents at the jthlocal window;and M is the number of local windows of the image.

We choose the image Lena as the test targetand compare the proposed algorithm with several state-ofthe-art algorithms.We choose the GPSR-bb algorithm as GPSR algorithm.

The parameters for the proposed algorithm are λ0=10，k=0.8.The parameters for the others are defaults in the papers by the authors.The parameters for the GPSR-bb algorithm areαmin=10-30，αmax=1030，λ=0.35.The parameters for the SpaRSA-monotone algorithm areλ=0.035，M=0，σ= 10-5，η=2.The parameters for the Tw IST algorithm areα=1.960 8，β=3.921 2.The parameter for the SALSA algorithm isλ=0.025.The parameter for the FTVd algorithm isλ=50 000.

For all the algorithms，we choose the same maximum iteration number as 10000;the same stop criterion as the relative error difference between two iterations is less than 1×10-7.All computations were performed under windows7 and matlab V 7.10（R2012a）running on a desktop computer with an Intel Core 530 duo CPU i3 and 2GB ofmemory.

Where X and Y are the original and the reconstructed images，respectively;μxandμyare themean intensity，σxandσyare the standard deviation;and σxyis the covariance.

Where L is the dynamic range of the pixel values（255 for 8-bit grayscale images），and K1and K2are small constants.

5.1 M otion degradation

We use thematlab function psf=fspecial（′motion′，71，56）to create the motion blurring kernel point spread function，and use g=im filter（f，psf，′conv′，′same′，′circular′）to get the motion blurred image，and use g=imnoise（g，′Gaussian′，0，1×-3）to add white Gaussian noise of zero mean and standard deviation 1×10-3.

In the Fig.2，there are 256 pixel×256 pixel original image Lena（a），motion blurring kernel noisy blurred image（b），image restored by the improved fixed pointmethod（c），GPSR-bb（d），SpaRSA-monotone（e），TwIST（f），SALSA（g）and FTVd（h）.

Fig.2 Restoration comparison ofmotion degradations

Tab.1 contains the MSSIM and time comparison between the proposed algorithm and several state-of-the-art algorithms with motion degradation.

Tab.1 Restoration com parison ofmotion degradations

5.2 Gaussian degradation

We use the matlab function psf=fspecial（′Gaussian′，［21，28］，10）to create the Gaussian blurring kernel point spread function，and use g= imfilter（f，psf，′conv′，′same′，′circular′）to get the Gaussian blurred image，and use g=imnoise（g，′Gaussian′，0，1×10-3）to add white Gaussian noise of zeromean and standard deviation 1×10-3.

Fig.3 Restoration comparison of Gaussian degradations

In the Fig.3，there are 256 pixel×256 pixel original image Lena（a），Gaussian blurring kernel noisy blurred image（b），image restored by the improved fixed point method（c），GPSR-bb（d），SpaRSA-monotone（e），Tw IST（f），SALSA（g）and FTVd（h）.

Tab.2 contains the MSSIM and the time comparison between the proposed algorithm and several state-of-the-art algorithms，with the Gaussian degradation.From the above comparisons，we can see that under the high noise level，the improved fixed point method performs better than the others，and the FTVd algorithm is totally unfit.

Tab.2 Restoration comparison of Gaussian degradations

6 Conclusion

We propose，analyze，and test the improved fixed pointmethod for solving the Tikhonov regularization under the periodic boundary conditions in image restoration problem.In experimental comparisons with state-of-the-art algorithms，the proposed algorithm achieves remarkable performance in both subjective and objective judgments of the image restoration ability.

［1］HANSEN PC，NAGY JG，DEBLURRING D P.Images：Matrices，Spectra，and Filtering［M］.Philadelphia：SIAM，Society for Industrial and Applied Mathematics，2006.

［2］DAUBECHIES I，FRIESEM D，MOL C D.An iterative thresholding algorithm for linear inverse problems with a sparsity constraint［J］.Communications in Pure and Applied Mathematics，2004，57：1413-1457.

［3］ELAD M，MATALON B，ZIBULEVSKY M.Image denoising with shrinkage and redundant representations［C］//Proc.of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition，CVPR″2006，New York，2006，2：1924-1931.

［4］FIGUEIREDOM，BIOUCAS-DIAS J，NOWAK R.Majorizationminimization algorithms forwavelet-based image restoration［J］.IEEE T.Image Process.，2007，16（12）：2980-2991.

［5］FIGUEIREDO M，NOWAK R.An EM algorithm for wavelet-based image restoration［J］.IEEE T.Image Process.，2003，12：906-916.

［6］FIGUEIREDO M，NOWAK R.A bound optimization approach to wavelet-based image deconvolution［C］//Proc.of the IEEE International Conference on Image Processing，ICIP′2005，Genoa，Italy，2005，2：782.

［7］RUDIN L，OSHER S，FATEMIE.Nonlinear total variation based noise removal algorithms［J］.Phys.D，1992，60（1-4）：259-268.

［8］RUDIN L，OSHER S.Total variation based image restoration with free local constraints［C］//Proc.of the IEEE International Conference on Image Processing，ICIP，1994，1：31-35.

［9］CHAMBOLLE A.An algorithm for total variationminimizationand applications［J］.J.Math.Imaging Vis.，2004，20：89-97.

［10］CHAN T，ESEDOGLU S，PARK F，et al..Recent developments in total variation image restoration：Handbook of Mathematical Models in Computer Vision［M］.New York：Springer Verlag，2005.

［11］FIGUEIREDO M A T，NOWAK R D，WRIGHT S J.Gradient projection for sparse reconstruction：application to compressed sensing and other inverse problems［J］.IEEE J.Selected Topics in Signal Processing，2007：586-597.

［12］WRIGHT S J，NOWAK R D，FIGUEIREDOM A T.Sparse reconstruction by separable approximation［J］.IEEE T.Signal Process.，2009，57（7）：2479-2493.

［13］BIOUCAS-DIAS J，FIGUEIREDO M.A new Tw IST：two-step iterative shrinkage/thresholding algorithms for image restoration［J］.IEEE T.Image Process.，2007，16（12）：2992-3004.

［14］BIOUCAS-DIAS J，FIGUEIREDO M.Two-step algorithms for linear inverse problems with non-quadratic regularization［C］//IEEE International Conference on Image Processing-ICIP′2007，Sept.16-Oct.10，2007，San Autonio，TX，2007，1：105-108.

［15］AFONSOM V，BIOUCAS-DIAS JM，FIGUEIREDOM A T.Fast image recovery using variable splitting and constrained optimization［J］.IEEE T.Image Process.，2010，19（9）：2345-2356.

［16］FIGUEIREDO M，BIOUCAS-DIAS JM，AFONSOM V.Fast frame-based image deconvolution using variable splitting and constrained optimization［C］//IEEEWorkshop on Statistical Signal Processing-SSP′2009，Aug.31-Sep.03，2009，Cardiff UK，2009.

［17］AFONSOM V，BIOUCAS-DIAS JM，FIGUEIREDOM A T.An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems［J］.IEEE T.Image Process.，2011，20（3）：681-695.

［18］AFONSOM V，BIOUCAS-DIAS JM，FIGUEIREDOM A T.A fast algorithm for the constrained formulation of compressive image reconstruction and other linear inverse problems［C］//IEEE International Conference on Acoustics，Speech，and Signal Processing（ICASSP），Mar.14-19，2010，Dallas，US，2010.

［19］WANG Y，YANG J，YINW，etal..A new alternatingminimization algorithm for total variation image reconstruction［J］. SIAM J.Imaging Sciences，2008，1（3）：248-272.

［20］YANG J，YINW，ZHANG Y，et al..A fast algorithm for edge-preserving variationalmultichannel image restoration［J］. SIAM J.Imaging Sciences，2009，2（2）：569-592.

［21］YANG J，ZHANG Y，YIN W.An efficient TVL1 algorithm for deblurring multichannel images corrupted by impulsive noise［J］.SIAM J.Sci.Compu.，2009，31（4）：2842-2865.

［22］TAO M，YANG J，HE B.Alternating direction algorithms for total variation deconvolution in image reconstruction［EB/ OL］（2009-06-07）.［2012-07-11］.http：//www.optimization-online.org/DB_HTML/2009/11/2463.html.

［23］VOGEL C R，OMAN M E.Iterative methods for total variation denoising［J］.SIAM J.Sci.Comput，17（1），227-238，1996.

［24］WANG Z，BOVIK A C，SHEIKH H R，et al..Image quality assessment：from error visibility to structural similarity［J］. IEEE T.Image Process.，2004，13（4）：600-612.

Authors′biographies：

YAN Xue-fei（1979—），male，PhD student.He received his B.S.degree in electronics engineering from Shanxi University in 2002，and received his M.S. degree in Optical Engineering from Beijing Institute of Technology in 2007.His research interests include image deblurring.E-mail：yxfamyself@sina.com

BAITing-zhu（1955—），male，M.PhD supervisor，Professor，PhD.He received his B.S.，M.S.and Ph.D.degrees in Optical Engineering from Beijing Institute of Technology in 1982，1987 and 2001，respectively.His research interests include electro-optical imaging technology，photoelectric detection technology，and image information processing technology.E-mail：tzhbai@bit.edu.cn

XU Ting-fa（1968—），male，M.PhD supervisor，Professor，post doctorate.He received his B.S.and M.S. degrees in physics from Northeast Normal University in 1992 and 2000，respectively，and received his Ph.D. degree in Optical Engineering from Changchun Institute of Optics，Fine Mechanics and Physics，Chinese A-cademy of Sciences in 2004.He finished studies in mobile postdoctoral station of South China University of Technology in 2006.His research interests include photoelectric imaging detection and recognition，target tracking，photoelectric measurement.E-mail：xutingfa@163.com

改进的固定点图像复原算法

阎雪飞，许廷发*，白廷柱
（北京理工大学光电学院光电成像技术与系统教育部重点实验室，北京100081）

研究了周期边界条件下，Tikhonov正则化的固定点算法，提出了变化正则化参数的方法。首先对正则化参数取较大值，抑制复原图像中的噪声，通过得出的收敛结果来修正初始梯度;然后对正则化参数取较小值，以增强复原图像中的细节。实验结果表明，与当前求解L1范数正则化函数和全变分正则化函数的流行算法比较，本文算法对于运动模糊与高斯模糊图像的复原效果更佳。

图像复原；周期边界条件；Tikhonov正则化；变正则化参数

TP391.4

A

1674-2915（2013）03-0318-07

2013-02-11；

2013-04-13

Major State Basic Research Development Program of China（973 Program，No.2009CB72400603）;The National Natural Science：Scientific Instrumentation Special Project（No.61027002）;The National Natural Science Foundation of China（No.60972100）

10.3788/CO.20130603.0318