基于小波分析的电线电缆故障信号特征提取

2013-04-25杜宏超

电子科技 2013年9期

杜宏超

(西安电子科技大学电子工程学院，陕西西安710071)

小波分析作为时间频域分析的一种新技术，近年来，取得了较大的发展。它以其自身优越的特性，在小波尺度分析和信号去噪两个方面，受到广大学者的青睐。近年来，电线电缆行业行业的蓬勃发展，逐渐引入了该项技术，并取得了一定的进展。小波分析技术为电线电缆故障特征信号提取提供了一种思路，具有较好的研究价值［1］。

1 理论引入

电缆故障的检测过程非常复杂，为提取有效的故障信息，准确判断故障类型，需要利用有效的噪声滤除技术对所提取的故障信号进行信号去噪，小波去噪技术就是一种有效的去噪方法。然而，如何选取合适的阈值进行去噪，需要根据输入信号的类型进行选择。

2 理论简介

2.1 小波去噪理论

首先建立小波去噪的一般理论模型:用f(i)表示原始信号，e(i)表示噪声信号，s(i)表示含噪信号，那么表示含噪信号的一维模型可以表示为s(i)=f(i)+σ·e(i)，i=0，1，…，n－1。模型中的噪声信号往往是一些高频信号，有用信号多为低频或一些平稳信号。为直观形象地表示出故障信号的特征提取过程，以3层小波分解为例，用一个简单的模型来表示信号去噪的过程。

图1中，S表示含噪信号，cal、ca2、ca3分别表示信号分解后的第1、2、3层的低频信号，用cdl、cd2、cd3分别表示分解后第1、2、3层的高频信号。对信号S去噪的本质就是抑制信号中的高频信号部分，尽可能多地恢复出低频信号部分。恢复低频信号，就可以有效地增加实际有用信号在总体中所占有的比例，这样可以提高有用信号比例并且可以保证仿真试验中信号数据的可靠性。

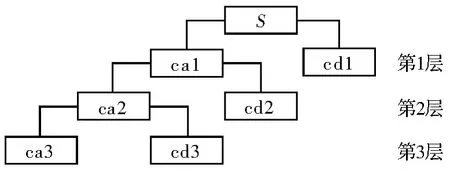
图1 信号的3层小波分解图

2.2 实现步骤

(1)对原始信号进行小波分解。确定小波函数并且选取小波分解层数N，对信号进行N层的小波分解。

(2)对小波分解后高频信号部分作阈值处理。选取一种合适的阈值处理方法对每一层的高频系数作量化处理。

(3)信号的小波重构。对经过小波分解阈值量化处理后每一层的低频信号部分作小波信号重构，得到去噪后所得的信号。

目前常用的阈值量化处理方法有4种，分别是基于Sqtwolog规则的通用阈值、基于Rigrsure规则的Stein无偏似然估计阈值、基于Heursure规则的Stein无偏风险阈值和基于Minimax规则的最大最小准则阈值。采用Rigrsure规则去噪后得到的信号中依然包含很大部分的噪声信号，而基于其他3种阈值规则下信号去噪以后，虽然滤除噪声的效果比Rigrsure规则更好，但并没有完全滤除噪声，而且与此同时也滤除了部分有用信号［2］。因此引入基于阈值的3σ去噪方法，该方法能够满足信号提取的要求并根据需要得到信号中的有用部分。

3 试验仿真

3.1 基于阈值去噪原理

第一步，得到电线电缆故障特征信号:把电线电缆故障信进行N层小波分解，得到高频信号部分和低频信号部分，进而选取一种合适的阈值处理方法对每一层的高频信号系数进行量化处理，并保持低频信号不变。最后对小波分解经过阈值量化处理后的每一层低频信号部分作小波信号重构，从而得到去噪后的电缆故障特征信号。

第二步，对得到的故障特征信号进行小波去噪。一般来讲，大多采用固定的软阈值方法，假设电缆的特征信号为S={si}，i=1，2，…，L，其中L表示采样长度。噪声干扰信号用W=BN(0，σ2)来表示，用σ2表示噪声的强度，则含噪的电线电缆故障信号可以表示为X=S+W。基本步骤如下:

(1)对电缆故障信号X进行n层小波分解X=an+dn+dn－1+…+d1，其中an表示信号分解后的低频信号部分的小波系数，而{dj}，j=1，2，…，n，表示小波分解后高频信号部分的小波系数。

(3)根据thr对{dj}进行处理。

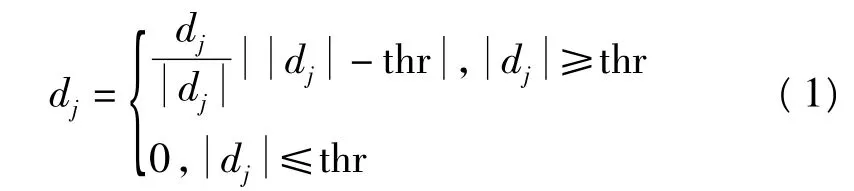
最后，根据和an和{dj}进行小波重构，提取出滤除噪声后的电缆故障特征信号。

3.2 3σ小波去噪实施过程

实验表明，基于阈值的去噪方法在一定程度上滤除了电线电缆故障信号的部分有用信号，导致实验结果并不理想。为更好地保留有用信号，即电缆特征信号，采用一种基于阈值的只处理噪声信号的噪声判断方法，即3σ小波去噪方法［3］。3σ小波去噪步骤如下:

(1)确定小波分解层数。需要考虑的问题:小波去噪的效果跟分解层数的选择有较大关系，通常情况下，分解层数越多，对各层小波空间的系数做阈值处理时低频信号部分中的有用信号丢失越严重，因此需要特别注意层数的选择。层数的选择不是越多越好，也不是越少越好，需要根据故障信号的种类进行选择，同时还要考虑整个电路的实际情况。本仿真实验采用正弦信号作为含噪信号，根据经验，确定5层小波分解为最优的分解层数［4］。

(2)判断各层噪声信号。因为一维模型中加入的噪声信号是白噪声，所以需要注意白噪声的一些特性。鉴于独立的白噪声是一个随机过程，所以当电缆故障信号长度逐渐接近无穷大时，故障信号的自相关系数具有如下特征

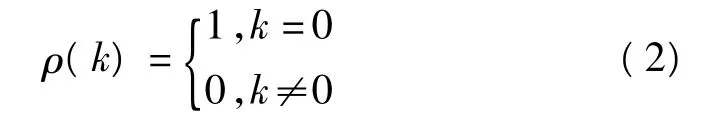
假设第j层小波分解后的离散信号序列为{di，j}，i=1，2，…，L，其自相关系数的估计值为

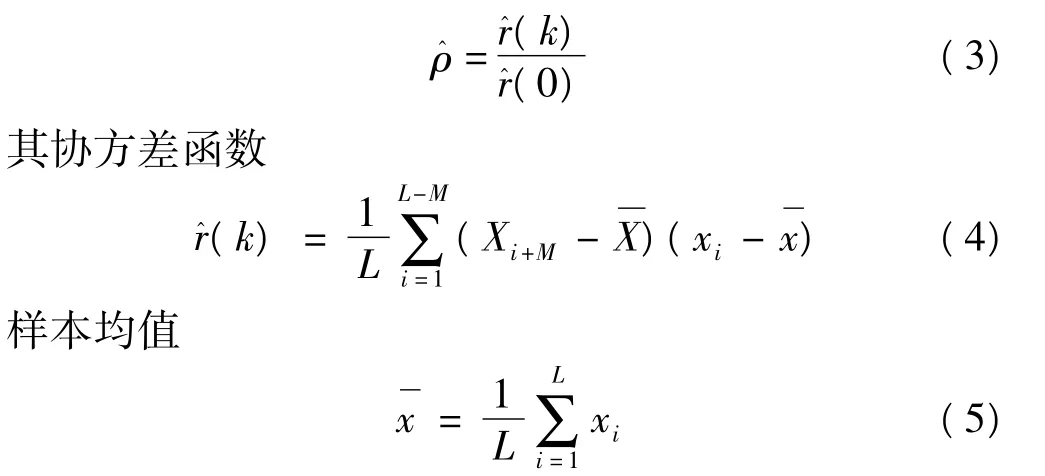
其中，k=l，2，…，M，l＜M＜L，采样长度用L表示。

(3)选择阈值。首先计算概率，根据数理统计知识可知

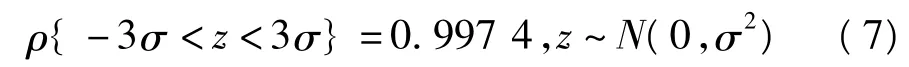
仿真中加入的噪声信号是白噪声，它的方差为σ2，但其方差值很难测得，这里根据离散小波序列的方差2来预测噪声信号的方差σ2，设定阈值为32。

(4)根据thr={dj}对小波系数序列{dj}进行处理。

(5)根据an和{dj}进行对各层小波系数进行小波重构，从而滤除噪声，提取出电缆故障的特征信号。

3.3 仿真及结果

按照之前确定的步骤，设定分解层数为5层，故障信号为正弦信号，用Matlab进行图像仿真。图像结果的好坏直接表明3σ小波去噪方法在电缆故障特征信号的提取中是否具有实际的可行性。

信号为

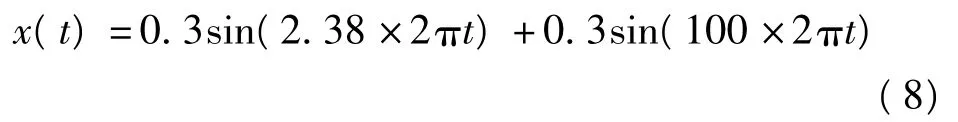
加入的白噪声为

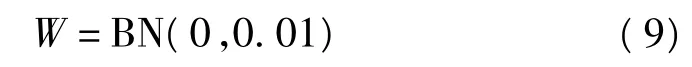
仿真结果如图2所示。

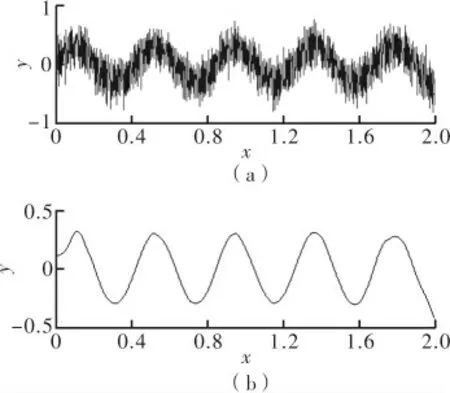
图2 默认阈值去噪和3σ去噪后的信号波形比较图

如图2所示，前者故障信号中的高频部分被部分忽略，信号损失严重，该高频部分对最终结果比较重要，这种方法不能达到预期效果。而后者波形比较平滑，是比较理想的去噪后波形图，这表明3σ去噪方法能够较好地滤除噪声信号，对故障信号的有用部分进行了很好的保护，达到了滤除噪声同时不损害原有信号的目的。因此，基于阈值的3σ去噪方法对电线电缆故障信号提取优势明显。