一种基于ABT树的忽略缓存算法

肖 瑜，刘宏义，杨 明

(中国人民解放军边防学院 战术教研室，陕西 西安710108)

计算机体系结构所描述的多级存储系统正不断变得越来越慢、越来越大。这个多级存储系统包括寄存器、一级缓存、二级缓存、主存和硬盘。它们的访问时间从寄存器的一个存储周期，增长到了缓存、主存和硬盘各自的10、100和100 000个存储周期。从当前CPU及内存的发展情况来看，那些不能充分利用这个多级存储结构的算法，会有更多的缓存缺失，从而造成更严重的后果。为了解决这个问题，文献［1］提出了忽略缓存的算法。该算法的核心思想是在不需要预知存储块大小的情况下优化I/O模型的方案。

1 内存结构

大多数算法都会忽略内存结构。如二叉树，在访问它们的数据时会遭受严重的性能下降。每一个内存层都是以相似的方式工作，并由缓存块组成。当前的内存结构使用的缓存行的大小是32～64个Byte，通过访问同一个缓存行中的数据，可以获得明显的性能提升［2－3］。缓存的管理要选择合适的替换和关联策略。有时，缓存缺失是不可避免的，例如强制缺失、容量缺失、冲突缺失［4］空间的排列对缓存的使用影响较大。特别要注意的是，密集使用指针的数据结构并不是好的选择。可能需要一起访问的指针或数据，最好也保存在一起，这样可以优化内存的访问［5－6］。在某些情况下，它们也许无法遵从面向对象编程的方法论。Van Emde Boas布局［7］是一个内存中编排出平衡树的标准方法，如图1所示。在忽略缓存的模型中，使用它可以高效地遍历从根节点到叶子节点的每一条路径，其时间复杂度为O(4×logB(N))次内存传输，其中B=NbElement/CacheLine。

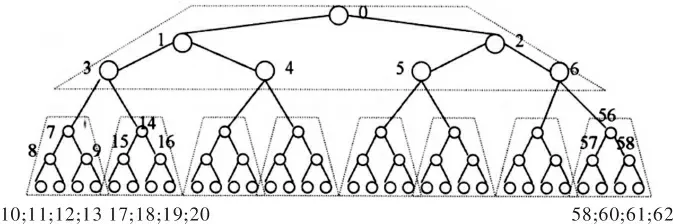
图1 Van Emde Boas树的表示法

2 实现ABT树

ABT树与KD树类似［8］。在每个构建步骤中，沿坐标轴的分割平面会分割出两个子节点。与KD树有一点不同的是，ABT树的算法可以将分割产生的子节点的AABB盒最小化，并将所有几何体独占式地存储在叶子节点中。这样，每个节点就变成了空间中一个完全封闭的区域。在这个空间中，会遍历这些内部节点，将场景中的不可见部分剔除。

2.1 ABT树的创建

创建ABT树是从一个根节点开始，这个根节点包含一个对整个场景AABB盒的引用。递归创建法会用一个轴向上的分割平面，将局部当前节点的AABB盒分割成两个部分(2个面)，然后根据它们的中间层，把这两个面分别分配给两个子节点，如图2所示。

图2 沿坐标轴的包围盒的重新调整

一旦所有面都分配完毕，每个子节点就会重新计算它们各自的、含有这个层中独一无二的面的AABB盒，分割策略会尽量将下列属性最小化。

空间局部化，如式(1)所示

树的平衡性，如式(2)和式(3)所示

在性能出现显著降低之前，Epsilon应该维持在5%～10%以下。在多数情况下，将AABB场景复杂度扩展5%，就可以包含90%的面，如式(4)和式(5)所示

最后的公式如式(6)所示

根据游戏引擎的瓶颈和场景的组织，公式中各项的权重会有所变化。在预处理阶段和运行时，采用的方法也不同。在运行时，在不同的渲染阶段，每个视点通常都会执行一个完全或部分的遍历。从上一个局部根节点开始，递归函数会检测两个子节点是否位于视锥内部，如果确实位于视锥内部，那就继续执行树的遍历。当遍历到一个叶子节点时，它包含的所有几何体都可以传送到渲染管道中的下一个阶段。由于每个面都是独一无二的，所以不需要进行额外的测试。还可为叶子节点和局部素材维护一个微小的顶点缓冲器。为了减少所使用的顶点缓冲器的数量，我们可以从邻居子节点的位置中获益。因此，几个叶子节点可以共享一个单独的顶点缓冲器，只要不超出顶点缓冲器的容量限制即可。这样一来，当几个邻居节点需要一起处理时，就可以获得更高效的分支处理，提高渲染性能［9］。

2.2 效率和复杂度

所有二叉树，特别是BSP树和KD树，都会受到树的深度困扰。即使ABT树的处理能力优秀，树的深度也依然是个重要问题。假设树的实现是使用指针，而不是隐式指针，那么可以认为每当树要沿用一个指针时，就会发生CPU的缓存缺失。相对于树的深度，缓存缺失的数量会相应地增加到一个极限值，这时缓存缺失变得比交叉检测的代价还大。然而，忽略缓存的树会减少与缓存行大小有关的缓存缺失，树的遍历工作也变得对内存访问而不是对CPU性能不太敏感了。

与所有的二叉树一样，ABT树也需要一个O(logn)的搜索时间［10］。通过使用Van Boas忽略缓存的布局表示法，搜索时间可以估算为O(4×logB(n))。其中，B=CoupleNode÷CacheLines如图3所示［11］。

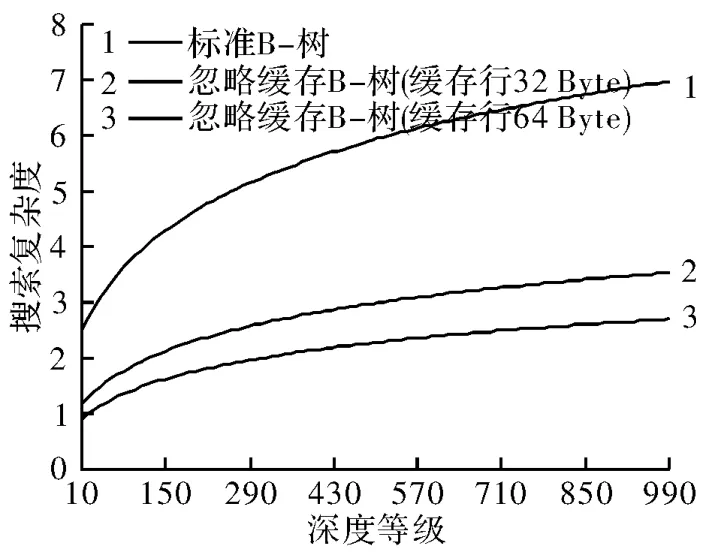
图3 搜索时间排序

每个节点需要存储各自的局部AABB盒和一个指向其两个子节点的指针。AABB盒由6个浮点值表示是6×4个Byte，指向两个子节点的指针是2×4个Byte(32位CPU)，或者2×8个Byte(64位CPU)。这样每个节点的内存总需求是32个Byte(32位CPU)，或者40个Byte(64位CPU)。如果使用一个不成熟的算法，内存消耗相对更重要。文献［12］指出只需保存每个子节点AABB盒的相对范围(Extent)，可以把每个范围压缩成一个8位的整数值。这个谨慎的估算方法只有1/255，也就是约0.4%的相对误差，完全可以被平均5%～10%的AABB重叠率覆盖。

2.3 冗余技术

为减少内存开销，在每次分割时，定义子节点AABB盒12个范围(Extent)中的6个直接来自父节点，因为父节点包含的所有面都会被分割、传递给叶子节点。不是单独为每个子节点保存几个Byte的信息，而是把两个子节点保存为一个整体。这样，就不用局部地保存每个子节点AABB盒的绝对数据，取代它的是每对子节点都会保存它们相对于父节点AABB盒的一个比例。因此，需要有6个Byte来表示子节点的相对比例。通过不同特征指定的另一个Byte会使用两个子节点的相对位置，并再次使用父节点的相关数据。在运行时的遍历过程中，递归方法会重新计算子节点局部AABB盒的位置。因为在此阶段最后一个Byte还有两位没有用到，所以就用这两位来说明左/右子节点是右节点还是叶子节点，如图4所示。

图4 ABT树的节点数据表示(一对子节点)

为了遵守忽略缓存算法的数据结构定义，把这些数据都保存为8个Byte的一个值，为树本身留下7个未使用的位(bit)。例如，可以使用这7个位(bit)来标识是否加载了下列子树(Subtree)，这对流(Streaming)应用具有一定价值。最后，因为子树总是2的幂减去1，且缓存行的大小也总是2的幂，所以有8个Byte可以用来把这棵子树链接到下一棵子树。由于打算用隐式指针来表示这种分级，所以用4个Byte来保存第1个可用子节点的索引。另外4个Byte中，有些位用来说明哪个端节点(End node)连接在子节点的子树上。根据不同缓存行的大小，有些位可能仍然未被使用，如图5所示。

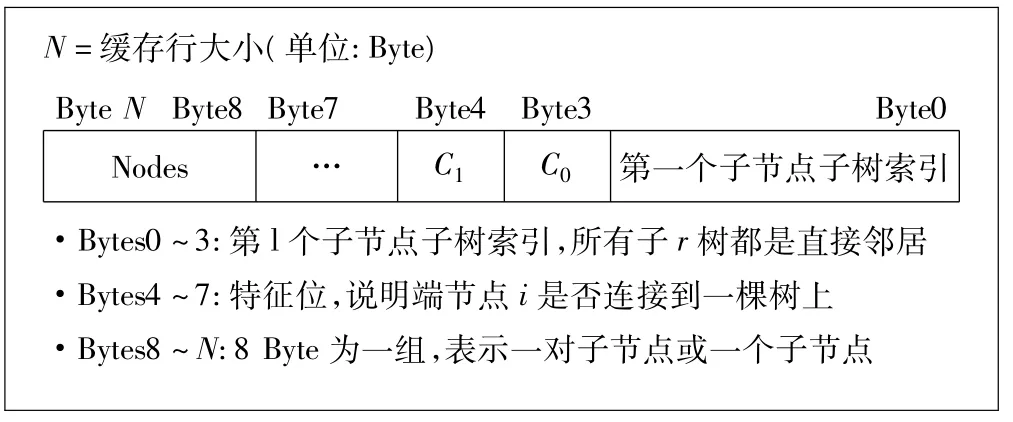
图5 缓存行的组织结构

当上一棵子树的所有子树都成为直接邻居时，这个创建过程就完成了，如图6所示。考虑叶子节点，它也是由8个Byte组成。一个位用来表示它的条件，在32位系统中，31个位就足够了，留出4个Byte可以用来保存其他的附加信息。

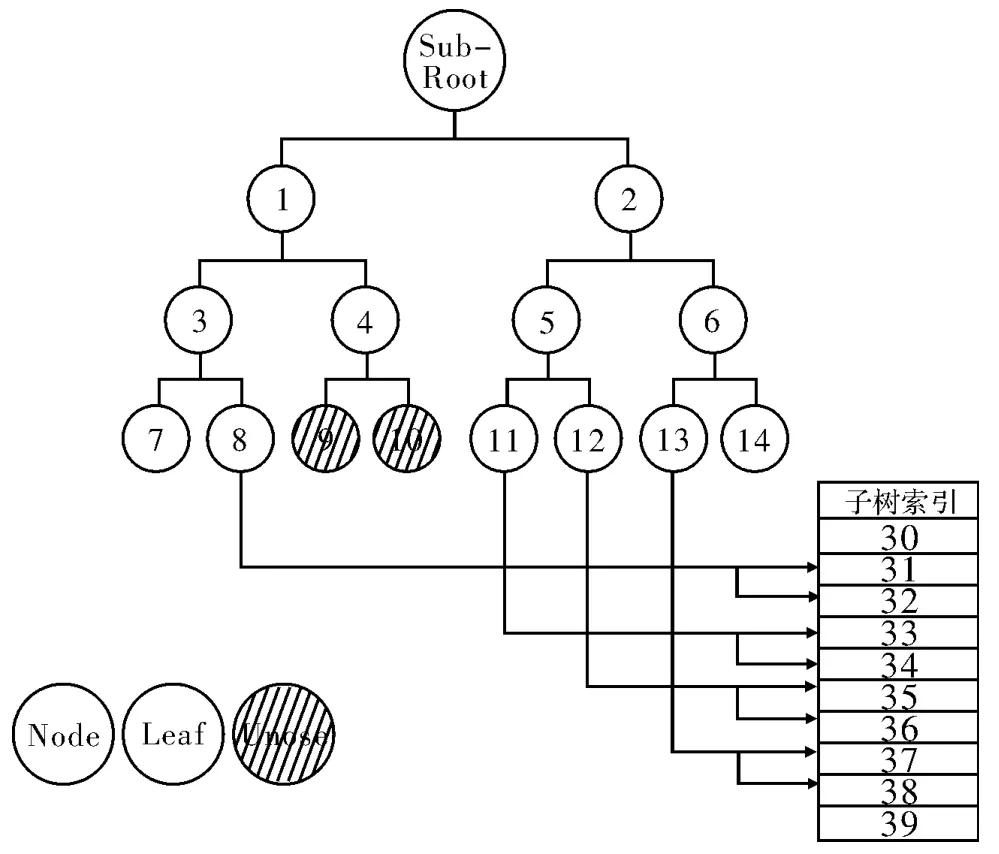
图6 子树的组织结构以及到次级子树的链接

图7 ABT树的叶子节点的数据表示

2.4 性能分析

为了分析这种方法的性能，使用了3个不同的实现算法进行实验，其内存使用情况如图8所示。直觉算法:6×4个Byte用来保存AABB盒，8个Byte用于保存指向子节点的指针，或者用64个Byte保存一对子节点。

图8 3个不同实现算法的内存使用情况

采用冗余技术:8个Byte用来保存AABB盒，8个Byte用来保存指向子节点的指针，或者48个Byte用来保存一对子节点。

忽略缓存算法(缓存行大小为64个Byte):每一对节点需要8个Byte，外加8/7个Byte用来保存隐式指针，平均下来是9.14个Byte。全局内存需求取决于树的平衡性，如图6所示。

3 结束语

虽然本文专注于讨论剔除算法，但ABT树在其他领域也是具有一定作用的，包括AI和3D音效管理。当前的硬件技术发展，CPU的速度会大幅提升，但是内存的发展却相对滞后，计算机的性能将会变得越来越依赖于内存访问，而不是单纯的CPU原始性能。实时仿真需要大量的数据集，而内存瓶颈会成为它的限制，CPU发展所带来的优点也会因此而弱化。但是，忽略缓存的算法具有良好的适应性，它为缓存感知算法提供了一个优良的替代方案，且二者的性能基本相同。

［1］FRIGO，LEISERSON，RAMACHANDRAN P.Cache－oblivious algorithms［C］.In Proc.40th Annual Symposium on Foundations of Computer Science(EOCS)，1999:285－297.

［2］PATTERSON，HENNESSY.Computer organization and design the hardware/software interface［M］.USA MA:Morgan Kanfmann，1997.

［3］HENNESSY，PATTERSON.Computer architecture:a quantitative approach［M］.USA MA:Morgan Kaufmann Publishers Inc，2003.

［4］HILL L.Cache performance［D］.USA Ulta:University of Wisconsin—Madison，2002.

［5］ERICSON，CHRISTEr.Memory optimization［C］.CDC2003，Santa Monica:Sony Computer Entertainment，2003.

［6］DING C.Data layout optimizations，computer organization［M］.NY:Lecture，Rochester，2004.

［7］VAN EMDE P BOAS.Preserving order in a forest in less than logarithmic time and linear space［C］.Information Process Letter，1977(6):80－82.

［8］SZECSI.An effective implementation of the K－D yree［M］.USA:In Graphics Programming Methods，Charles River Media，2003.

［9］WLOKA MATTHIAS.Batch，batch，batch:what does it really mean?［C］.Presentation at Game Developers Conference，2003.

［10］SEDGEWICK.Algorithm s in C［M］.USA:Addison Wesley，1990.

［11］BRODAL.Cache oblivious searching and sorting［M］.Copenhagen，Denmark: Seminar，ITUniversity of Copenhagen，2003.

［12］GOMEZ，LOURA.Compressed axis－aligned bounding box trees［M］.Copenhagen，Denmark:Charles River Media，2001.