基于障碍物地平角点的移动机器人定位*

郭丙华，李中华

(1肇庆学院电子信息工程系，广东 肇庆 526061;2.中山大学信息科学与技术学院，广东 广州 510006)

移动机器人定位是移动机器人研究领域的一项非常重要内容，移动机器人为完成某些任务，常常首先考虑的是自身的定位问题。针对这个问题，研究人员提出了许多定位算法，基于路标定位是其常用的一种方法，其采用的路标有两种，一种是在特定的位置人工放置特殊的路标，通过传感器对路标的识别来实现移动机器人的位姿估计。如文[1]的编码路标，文[2]人为放置的不同宽度的圆环路标。由于需要在特殊的位置放置特别的路标，因而使得移动机器人的应用受到限制。另一种是采用传感器提取环境中的某些特定标记作为路标，如文[3]在室内环境中通过视觉传感器提取天花板上规则的平行线以及其相交的角点作为移动机器人定位的路标。文[4]利用视觉传感器提取环境中的SIFT(Scale Invariant Feature Transform)特征点作为移动机器人的定位路标点。由于SIFT特征点的复杂性以及数量太多，其计算的复杂性随之增大。文[5]提取环境中的SURF和U-SURF特征点并将其应用于移动机器人的长时间室外环境定位，其实验结果证明采用SURF和U-SURF特征点的定位速度要优于SIFT特征点。文[6]则利用环境中的角点，采用RANSAC算法进行路径估计，由于角点简单，其定位算法的速度要快于采用SIFT和SURF特征点。

根据三角测量原理，三个路标点可以确定移动机器人在环境中的位姿[7]，路标点越多，采用定位算法估计的精度也越高，但算法计算的复杂度也越大。文[8]利用图论模型(Graph-theoretic Formulation)提出了一种用于移动机器人定位的特征路标点数量最优选择算法，显著降低了用于定位所需的路标数量，但运动前需要传感器预先离线获取环境数据。

移动机器人的工作环境不可避免存在各种障碍物，障碍物与地平面的交界轮廓边缘存在稳定的局部不变特征，而且这些特征只占整个环境中特征数量的小部分，以这些特征点作为移动机器人定位的路标点，其计算的复杂度将大幅度降低。本文采用立体视觉方法，结合Harris-Laplace算子、快速均值漂移方法构建了一个环境中障碍物与地平面交界轮廓的特征角点提取算法，即障碍物地平角点提取算法提取地平角点，并以这些角点为路标点结合自适应粒子滤波方法(APF)，实现移动机器人的位置估计。由于自适应粒子滤波方法的高效和鲁棒特性，以及路标点(障碍物地平角点)大幅度的减少，因而可以使移动机器人在其运动的环境中实现快速、准确的自主定位。

1 场景3D重建模型

采用三角测量原理，立体视觉可以重建场景的3D信息。若以移动机器人的中心为坐标中心，根据摄像机的配置和投影关系[9]，当不考虑摄像头的畸变时，可以得到图像平面坐标(u,v)和场景3D坐标(xw,yw,zw)的关系式：

(1)

其中(u0,v0)为图像平面的中心点坐标，B和h分别为左右摄像机的间距和安装高度，m0和n0为摄像机在移动机器人坐标系的水平安装位置，f为摄像机的焦距，D为左右摄像机图像对的视差值，ux和uy为CCD单位像数长度。

通过上述方程(1)可以找到移动机器人空间点在图像中的对应点。由于移动机器人工作的环境不可避免存在各种障碍物，为了利用方程(1)快速分离出障碍物地平角点，作如下约束：①移动机器人移动的平面为水平面;②场景中的障碍物定义为高出水平面的物体。这些约束对移动机器人工作于室内的环境来说是合理的。针对移动机器人工作的环境，提取的角点可以分为位于地平面上的角点PG和除此以外位于障碍物上的角点PO，考虑角点提取误差，我们对提取的角点Pi(xi,yi,zi)如果满足下式，则确定为地平面上角点，即

Pi(xi,yi,zi|zi<δ)⊂PG

(2)

其中δ为给定的阀值。在方程(1)中，yw为环境的深度坐标，各角点距离摄像头的深度yi可由下式得到

yi=yw-n0

(3)

2 障碍物地平角点提取算法

角点是环境中存在的一类重要的局部不变特征点[10]，其表现在目标轮廓线上曲率的局部极大，具有旋转、平移、缩放不变的性质，且计算量小，因而被广泛应用于图像配准与匹配、目标识别等方面，在此我们将其作为环境的路标点用于移动机器人的位姿估计。角点的提取常用Harris算子[10]，Harris算子具有平移和旋转不变性，且对光照不敏感，但不具有尺度不变性，由于移动机器人在移动过程中，障碍物相对移动机器人，其尺度可能发生变化，我们拟采用Harris-Laplace算子[11]提取角点。在移动机器人整个工作环境中存在大量的角点，为了降低因大量的角点带来的复杂计算，我们仅仅提取障碍物地平角点作为定位的路标点。

为了提取障碍物地平角点，我们拟借助于三维的立体视觉重构。由于采用Harris-Laplace算子提取的环境角点位于场景中的不同的位置，为了获得所需的障碍物地平角点，需要去掉多余的角点。在此我们采用均值漂移方法对角点进行类聚，具体利用文[12]提供的快速均值漂移分割算法得到各个区域，由角点所处的区域进行角点类聚，并对类聚的角点采用最小二乘方法进行平面拟合。假定拟合的平面方程为：

zk=akx+bky+ck

(4)

式中k为拟合的第k个平面，ak、bk和ck分别为平面系数。若地平面的角点为Pi(xi,yi,0)，则障碍物地平角点也满足方程(4)。但由于存在各种误差，我们采用下式确定障碍物地平角点，即Pi到方程(4)的距离d满足

(5)

式中δ为给定的阀值，可由具体的实验确定。

障碍物地平角点的提取算法具体如下：

1) 采用Harris-Laplace算子提取场景角点。

2) 利用立体视觉匹配得到视差，并对角点进行3D重构，根据角点位置由方程(2)得到地平面的角点和其它角点。

3) 采用快速均值漂移分割方法对环境区域分割，并对分割后同一区域的角点进行聚类，再对类聚的角点进行平面拟合，得到平面方程(4)。

4) 对地平面角点利用方程(5)去掉多余的角点。

由上述算法得到的障碍物地平角点将用于下述的粒子滤波定位。

3 粒子滤波

粒子滤波(PF)是以贝叶斯滤波算法为基础[13]，其采用随机采样方式并以样本的估计来逼近后验概率密度，在鲁棒性和定位精度上具有较大的优势。

假定移动机器人的位姿状态χ可以用下式表示

χ={x,y,θ}

(6)

其中x,y为移动机器人的位置，θ为方向，并且状态χ符合Markov假设。假定移动机器人在k时刻信度为Bel(χk)，则有

Bel(χk)=p(χk|z0～k)

(7)

z0～k表示0～k时刻的观测结果，p(χk|z0～k)状态预测估计的后验概率。根据贝叶斯规则，可得

(8)

其中η=1/p(z0～k)，p(χk|χk-1)为状态转移概率密度，可以通过移动机器人的运动模型得到，p(zk|χk)为观测测量概率密度，可从立体视觉观测到的信息模型求得。对于方程(8)，粒子滤波方法采用一组加权的粒子集来表示位姿空间的概率分布，即：

(9)

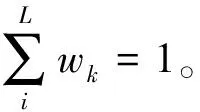
4 运动模型与观测模型

粒子滤波方法通过运动模型和观测模型更新粒子分布，假定移动机器人采用两后轮独立驱动，两后轮的角位移用旋转编码器测定，则其运动模型可用下式表示

(10)

其中mk-1，nk-1分别为在(k-1)时刻左、右轮的旋转编码器所测量出的脉冲个数，Mp为轮子转动一周的脉冲个数，R、T分别为轮子半径和两轮子之间的宽度。取χk={xk,yk,θk}，设w(k-1)为随机噪声，则上式可表示为

χk=f(χk-1)+w(k-1)

(11)

移动机器人可以根据χk-1以及其分布按上述方程产生新的粒子分布，实现p(χk|χk-1)的预测过程。

粒子滤波进入校正阶段，需要利用观测模型来更新粒子的权重，通过提取较大权重的粒子得到真实的移动机器人位姿密度。观测模型的建立来源于前述障碍物地平角点提取算法得到的角点深度信息和位置信息。

障碍物地平角点的深度表现为特征角点距离移动机器人的远近。通过立体视觉方法，采用左右图像对匹配可以得到其视差，由方程(1)可以求得各个障碍物地平角点的深度信息。假定观测模型其概率符合高斯分布，则有

(12)

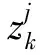
假定移动机器人在k时刻的中心坐标为(xc,yc)，其观测到的障碍物地平角点的位置由方程(1)转换到移动机器人的坐标系后为(xk,yk)，期望的距离为

(13)

移动机器人在k时刻观测概率密度可由下式得到

(14)

其中N为提取到的障碍物地平角点的数量。

5 应用与实验

由于粒子滤波方法的高效和鲁棒特性，针对移动机器人的运动模型和观测模型，我们采用粒子滤波算法来实现移动机器人的定位。为了有效降低计算的开销，我们采用Dieter Fox提出的自适应粒子滤波算法[14]来实现移动机器人定位。该方法采用后验概率分布与粒子集概率逼近之间的误差的K-L距离动态地调整粒子数目，当概率密度集中在状态空间的较小部分时采用较小的粒子数，否则采用较大的粒子数，具体细节参见文献[14]，在其算法中插入由运动模型和观测模型的数据更新。

移动机器人移动的地平面为水平面，图1为实验中的移动机器人和实验环境，移动机器人上安装的左右摄像头标定的内外参数矩阵如下：

左右摄像机的内参数分别为AL和AR，即

两摄像头之间的位置关系(旋转矩阵R和T平移矩阵)为：

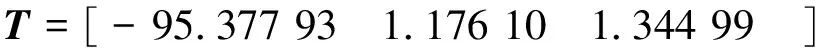
为了测试和验证本文提出的算法的性能，我们进行了一系列的实验，主要包括室内环境的定位实验和性能对比实验。实验中移动机器人的运动速度v≤0.5 m/s，方程(2)和方程(3)中取δ=10。整个算法是在Ti的DSP处理器(DM642)上运行，其中移植了部分OpenCv中函数库。

5.1 室内环境的定位实验

实验的室内环境见图1所示，图2～图6为实验测试的结果。图2为校正后的左右立体图像对，图3为通过立体图像对匹配算法得到的视差图，为了能够快速得到其视差图，我们采用了OpenCV[15]函数库中提供的块匹配函数 cvFindStereoCorrespondenceBM函数获得其视差，并利用cvReprojectImageTo3D函数重建特征角点的3D位置，从图中可以看到还有少量匹配不正确的位置，由于最终只需重建特征角点的3D位置，因而可以忽略。

图1 实验用的移动机器人和实验环境Fig.1 Mobile robot and experiment environment

图2 经过校正后的左右摄像机图像对Fig.2 Rectified stereo image pairs

图3 匹配后得到的视差图Fig.3 Disparity map

图4、5、6为采用上述的障碍物地平角点提取算法得到角点，最终得到的障碍物地平角点将作为路标用于移动机器人定位。图4为采用Harris-Laplace算子提取的所有环境角点。图5为采用均值漂移分割得到各个区域并对区域的角点进行平面方程拟合结果。图6中的“+”标记为最终得到的特征角点，比较图4和图6可以看到，用于定位的角点数量已大大减少。

图4 提取的Harris角点Fig.4 Extracted harris corner

图5 角点所在的平面Fig.5 Harris corner plane

图6 障碍物地平角点图Fig.6 Obstacle ground corner

图7为移动机器人在实验环境中的定位轨迹图，其中蓝线为移动机器人移动的轨迹，红线为采用粒子滤波估计的轨迹。从图中可以看出，在拐弯处实际轨迹与估计轨迹误差比较大，这可能是移动机器人在拐弯时容易发生滑动。由于立体视觉计算出角点的深度其误差随着距离的增大而变大，为提高估计的精度，对深度距离超过4 m的角点不予考虑。

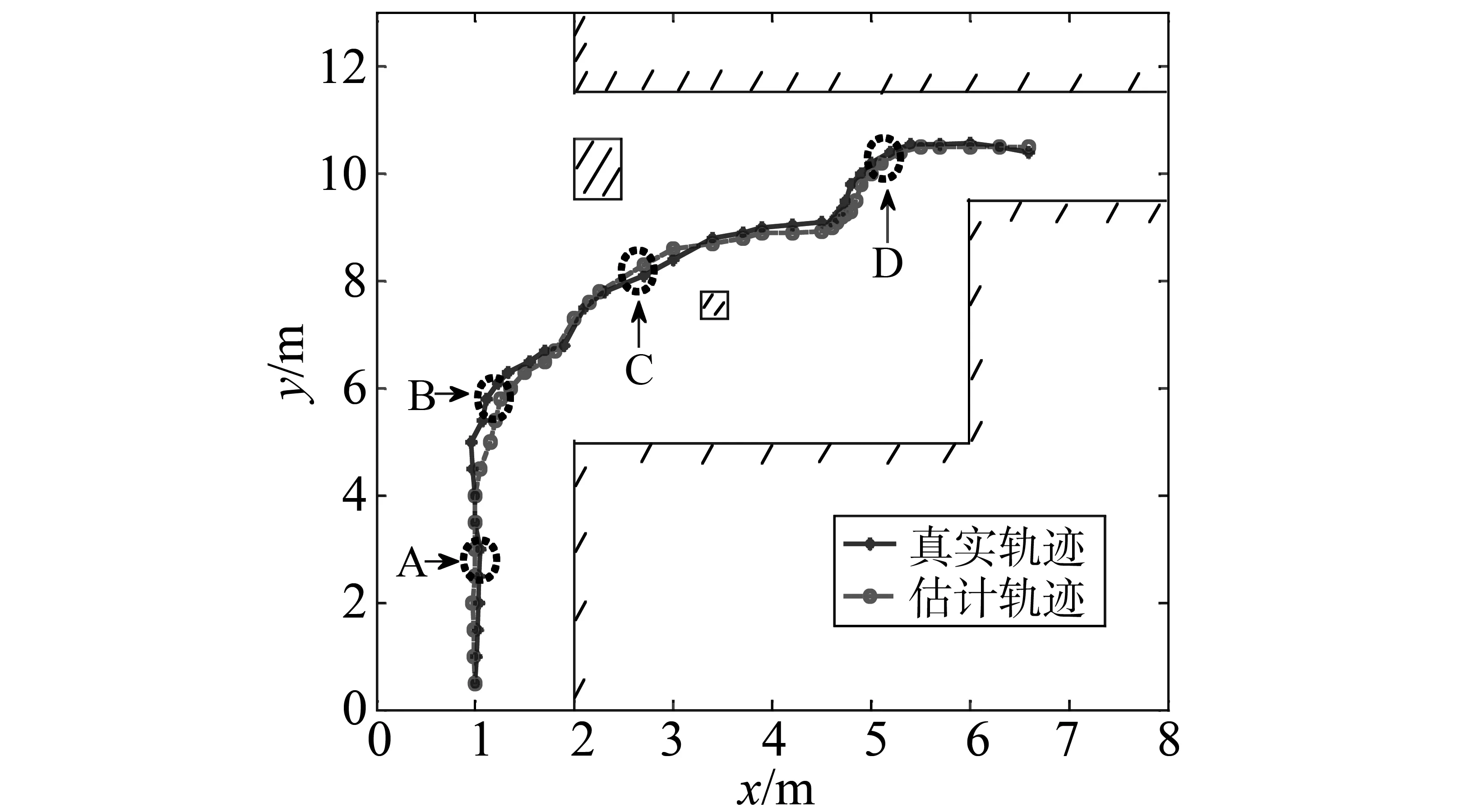
图7 定位的环境和轨迹图Fig.7 Trajectory of the mobile robot

5.2 性能对比实验

为了测试算法的性能，我们采用了环境中的SIFT、SURF、角点(Harris)和地平角点等特征点进行了实验，在移动机器人运动的路径上我们选取了4个位置进行性能对比，见图7中A、B、C和D标识，其中A位置近似直线运动，B位置大拐弯运动，C位置面对多个障碍物，D位置小拐弯运动，对比的性能包括算法运行的速度，定位的精度以及与文[6]所述算法的对比实验。

图8为移动机器人在上述4个位置提取的4种特征点的数量，其中地平角点的数量相对其它3种要少得多，图中超过4 m以外的特征点均已排除掉。

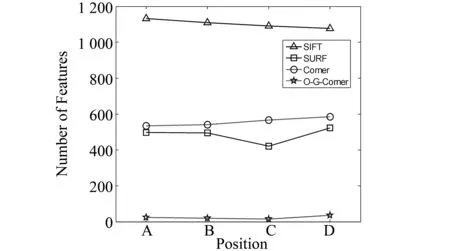
图8 4种特征点提取数量对比图Fig.8 4 Kinds of feature points extraction quantity

图9是在图7中的A、B、C和D 等4个位置分别提取SIFT、SURF、角点(Harris)和地平角点(O-G-Corner) 4种特征点用于本文的定位算法所需的时间图，图中带“▽”的连线为文[6]中利用环境角点采用RANSAC运动估计算法在上述4个位置定位所需的时间。从图中看出在算法速度上采用地平角点的定位算法要快于采用SIFT、SURF和角点特征点，与文[6]采用的算法相比较，完成定位所需的时间更少，在图9中，在A位置的定位所需的时间较大，这主要是由于粒子滤波定位初期，需要更多的粒子，因而完成定位需要更多的时间。

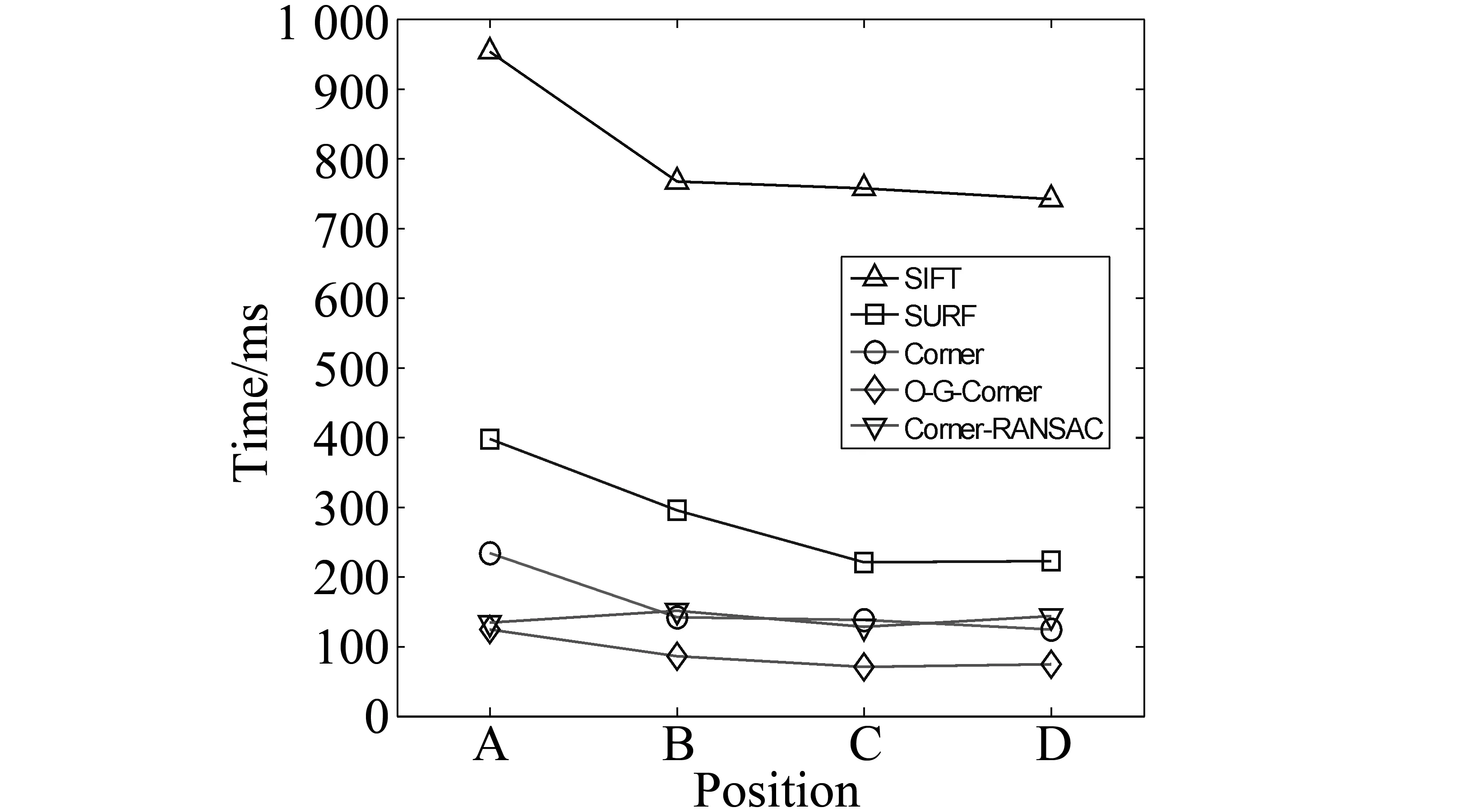
图9 算法运行时间对比图Fig.9 Run-time comparison

图10为本文算法在4个位置的定位精度，与文[6]中采用RANSAC运动估计算法一样均能达到较高的定位精度。

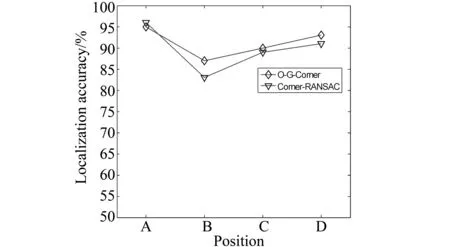
图10 算法定位精度图Fig.10 Localization accuracy comparison

6 结 论

角点是一类重要的局部不变特征点，而环境中不可避免存在障碍物，特别是在室内环境。与环境中存在的所有特征角点相比较，障碍物地平角点只占环境中角点数量的一小部分，以其为路标点可以实现移动机器人高效快速的定位。本文采用立体视觉方法，结合Harris-Laplace算子和快速均值漂移方法提出了一种障碍物地平角点提取算法，并利用自适应粒子滤波方法融合障碍物地平角点的深度和位置信息，实现了移动机器人高效快速和较为精确的定位，实验的结果证明了上述方法是行之有效的。

参考文献：

[1] 王景川, 陈卫东, 张栩. 一种鲁棒的室外移动机器人路标定位系统[J], 上海交通大学学报, 2010, 44(9):1181-1186.

[2] TWEDDLE B. Computer vision based navigation for spacecraft proximity operations[D]. Cambridge, USA: Massachusetts Institute of Technology, 2010.

[3] XU De, HAN Liwei, TAN Min, et al. Ceiling-based visual positioning for an indoor mobile robot with monocular

vision[J]. IEEE Transactions on Industrial Electronics, 2009, 56(5):1617-1628.

[4] CAMPOS F M, CORREIA L, CALADO J M F. Mobile robot global localization with non-quantized SIFT features[C]//The 15th International Conference on Advanced Robotics, Tallinn, Estonia : IEEE, 2011: 582-587.

[5] VALGREN C, LILIENTHAL A J. SIFT, SURF & seasons: appearance-based long-term localization in outdoor environments[J]. Robotics and Autonomous Systems, 2010, 58(2):149-156.

[7] BETKE M, GURVITS L. Mobile robot localization using landmarks[J]. IEEE Transactions on Robotics and Automation, 1997, 13(2):251-263.

[8] SALA P L, SIM R, SHOKOUFANDEH A, et al. Landmark selection for vision-based navigation[J]. IEEE Transactions on Robotics, 2006, 22(2):334-349.

[9] TSAI R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses[J]. IEEE J. Robotics and Automation. 1987, 3(4): 323-344.

[10] 熊会元, 宗志坚, 余志, 等. 基于凸包的棋盘格角点自动识别与定位方法[J]. 中山大学学报:自然科学版, 2009, 48(1):1-5.

[11] MIKOLAJCZYK K, SCHMID C. Scale & affine invariant interest point detectors[J]. International Journal of Computer Vision, 2004, 60( 1) :63-86.

[12] ARTHUR D,VASSILVITSKII S. K-means++: The advantages of careful seeding[C]//Proc. ACM-SIAM Symp. on Discrete Algorithms, New Orleans, Louisiana : IEEE, 2007: 1027-1035.

[13] THRUN S, BEETZ M, BENNEWITZ M, et al. Robust monte carlo localization for mobile robots[J]. Artificial Intelligence, 2000, 128(1/2): 99-141.

[14] FOX D. Adapting the sample size in particle filters through KLD-sampling[J]. International Journal of Robotics Research (IJRR), 2003, 22(12): 985-1004.

[15] BRADSKI G, KAEBLER A. Learning open CV[M]. 于仕琪, 刘瑞祯, 译. 北京: 清华大学出版社, 2011.