非连续正交频分复用系统次优导频设计

朱春华 杨 静 杨守义 穆晓敏 齐 林

(1.河南工业大学信息科学与工程学院，河南 郑州 450001；2.郑州大学信息工程学院，河南 郑州 450001 )

引 言

与传统正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)系统相比，非连续OFDM(Non-Continuous OFDM，NC-OFDM)系统中可用子载波的非连续性、非对称性和非固定性增加了用于信道估计的导频设计的复杂性.在NC-OFDM系统中，授权用户(Primary User，PU)占用的子载波被停用，这些被停用的子载波被称为零子载波.为避免对PU造成干扰，在零子载波位置，不能放置导频，所以OFDM系统中等间隔等功率的最优导频在NC-OFDM系统中不再适用.零子载波的存在破坏了导频的均匀性和对称性，而且由于PU的动态变化特性，零子载波的位置呈现非固定分布特性.因此，在NC-OFDM系统中，最优的导频图案必定是非固定、非均匀和非对称的，导频设计成为NC-OFDM系统的关键问题之一.在OFDM系统最优矩形导频图案的基础上，I.Rashad等[1-2]提出的移动导频设计以及Dong Xuetao等[3]建议的分组导频设计的思想依然是基于传统OFDM的导频设计，没有考虑NC-OFDM系统可用子载波分布的特点，可能不是最优的.

具有保护带或虚拟子载波的OFDM系统是NC-OFDM系统的一个特例，其可用子载波呈现的非连续对称分布特性导致该系统的最优导频是非均匀、非等功率分布的[4-7].代表性的方法是M.Ghogho[4]的穷搜索方法以及江彬等[5]和胡蝶等[6-7，9]等提出的次优导频设计方法.穷搜索方法的计算复杂度相当庞大，特别是当可用子载波数或信道长度较大时，在实际中难以实现；江彬等[5]和胡蝶等[7]通过利用信道估计均方误差(Mean Square Error，MSE)上界代替信道估计MSE的计算对其复杂度进行了一定程度的改进；然而，这种做法有可能会导致一种“虚假”的最优导频；而且文献[5]中搜索最优导频时是通过遗传算法来进行的，因此它也往往具有较高的复杂度；文献[9]则把优化求解过程转化为一系列一维搜索以减少穷搜索的计算量;与文献[9]所使用的方法相比，Robert J[8]的计算复杂度要更低一些.在导频位置的选择上，根据导频位置以直流分量(Direct Current，DC)为对称中心的特点，认为其在带内应该具有三次曲线的分布.因此，文献[8]通过将导频位置的搜索转换为对三次曲线系数的搜索，从而大大减少了运算复杂度.然而，这种算法是假定导频位置是以DC为中心对称的，而在应用认知无线电的NC-OFDM系统中可用子载波可能不是围绕DC对称时，文献[8]的导频设计就不再适用.

针对上述问题，本文提出了适用于认知无线电NC-OFDM系统的导频位置满足三次方函数关系的次优导频设计方法，能够降低导频搜索的计算复杂度并保持良好的信道估计性能.

1 系统描述

考虑认知无线电系统的下行链路，一个基站给PU和认知用户(Secondary User，SU)共同提供服务，采用IEEE 802.11a OFDM系统模型，并假定提供给SU接入的空闲频带与PU频带的使用情况如图1所示.图1中N是全部子载波数，i～j是PU占用子载波的索引号，PU占用的频谱资源是限制使用的，必须为其分配功率零，称作零子载波.因此SU可用子载波是非连续的，称这样的OFDM系统为NC-OFDM系统.

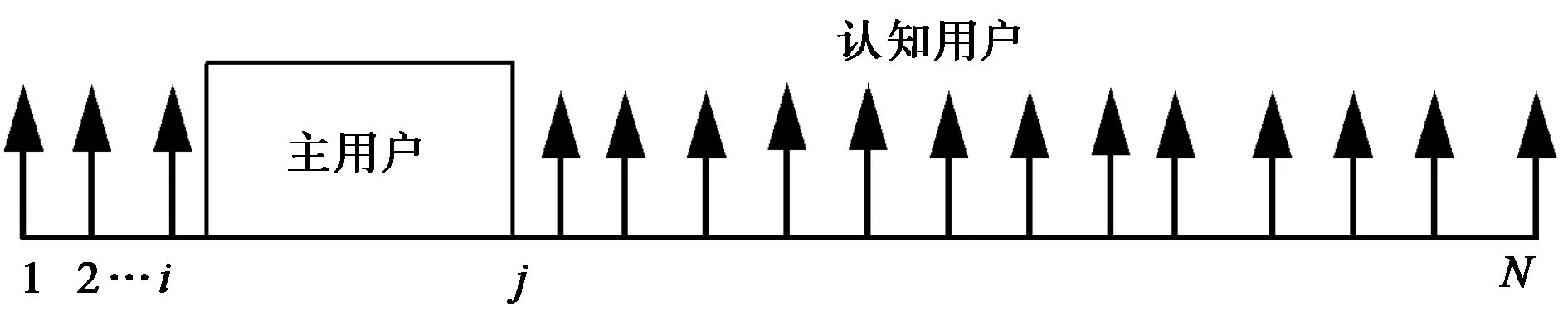
图1 PU与SU共存的频谱模型

图2 应用于认知无线电的NC-OFDM系统基带模型

应用于认知无线电的NC-OFDM系统基带模型如图2所示.与传统OFDM系统不同的是，SU在发射机中要进行频谱感知[10-12]，确定PU占用频带子载波，并利用剩余可用子载波进行通信.在接收机中，移除循环前缀，并进行快速傅里叶变换(Fast Fourier Transform，FFT)处理之后，接收信号可表示为

Y=DXH+W.

(1)

式中：DX=diag(X)为创建以X为主对角元素的对角矩阵,X=[x1，x2，…，xi-1，0，0，…，0，xj+1，…，xN-1，xN]是频域符号，其索引值属于集合ψ，ψ=κp∪κn∪κd， 其中κp、κn、κd分别是导频子载波、零子载波和数据子载波的索引号集合.NC-OFDM系统可用子载波索引号是1～i-1和j+1～N，且其数量Nc=N-j+i+1.H是信道频域响应，且有H=QLh，QL是Nc点FFT矩阵的前L列，h是L×1阶的时域信道冲激响应.W是高斯分布的白噪声矩阵.

由式(1)，接收的导频信号可表示为

Yp=DXpHp+Wp=DXpQph+Wp.

(2)

式中Xp、Yp、Hp和Wp分别是导频位置处的矩阵向量X、Y、H和W. 则h的最小二乘(Least Square，LS)估计值为

(3)

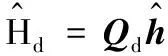
(4)

根据式(4)可得数据子载波信道LS估计的MSE为

(5)

式中：E[·]为数学期望; tr(·)是矩阵的迹运算;

(6)

当导频等功率分布时，式(6)可重写为

(7)

(8)

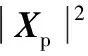
2 次优导频设计

由式(8)可知，导频的最优化设计包括两个步骤：

1) 导频位置优化设计.为了简化优化分析过程，本文首先通过一定的映射算法解决导频位置取值空间非连续分布问题，并假设导频位置满足三次曲线分布函数关系，求出最优的导频位置；

2) 在式(8)中以已知的导频位置为限制条件，对导频功率进行优化求解.

2.1 导频位置优化

频域符号X中从xj到xj的子载波是零子载波，这部分频率资源目前PU正在使用，因此导频位置的取值空间即X的索引号集合ψ可表示为

k∈ [1，2，…，i-1，0，0，…，0，j+1，…，N-1]，

(9)

示意图如图3.

图3 频域符号X的子载波索引号示意图

在认知无线电系统中，PU的动态变化特性决定了认知NC-OFDM系统本质不同于具有保护带的OFDM系统，认知NC-OFDM系统的可用子载波不再满足围绕DC对称分布的特性.那么如何将非对称非连续的子载波分布转化为连续对称分布的呢？本文采用的方法是以PU频带占用的子载波即零子载波频段的中心子载波作为对称中心，记为N0. 这样N0的位置将随着PU位置的不同而变化.如果子载波索引号大于N0，则把它与N的差记作新的子载波索引号，小于N0的子载波索引号不变，即

f(k)=k-N如果|k|>N0.

(10)

转化后连续分布的子载波索引号如图4所示.由图4所给的系统参数容易计算出子载波索引号的对称中心：

(11)

图4 转化后的频域符号X的子载波索引号示意图

图4所示映射后的子载波索引号f(k)可描述为

(12)

或

f∈ [j+1-N，…，-2，-1，0，1，2，…，i-1].

(13)

式中[N0-N，j-N]和[i，N0-1]这段零子载波被移动到子载波索引号的两端.这样就解决了式(8)导频最优化问题中优化变量搜索空间非连续导致的非凸问题，此时待优化求解的问题可描述为

(14)

g(τ)=a3τ3+a2τ2+a1τ+a0.

(15)

考虑导频设计的边缘效应，并进一步限制g(τ)，假设导频沿带内区域的中心对称分布.因此，可把索引号取值f再次映射为集合φ，

在集合φ上，函数g(τ)应满足关系

(16)

根据φ集合与f集合的取值对应关系，式(16)可重写为

(17)

求解式(17)，并利用式(10)的逆映射可找出g(τ)的实际导频索引号.假设a=j+1-N，b=i-1，则可求出函数g(τ)的各幂次系数，

(18)

由此，对式(14)的优化问题，通过搜索最优的a3可得出最优的导频位置.

2.2 导频功率优化

(19)

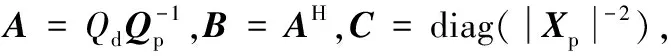
(20)

(21)

利用式(21)中的目标函数和限制条件构造拉格朗日函数

(22)

式中λ为待定系数.为使式(22)最小，可对其求一阶导数并令其等于零，从而推导得到最优的导频功率分布为

(23)

3 仿真实例

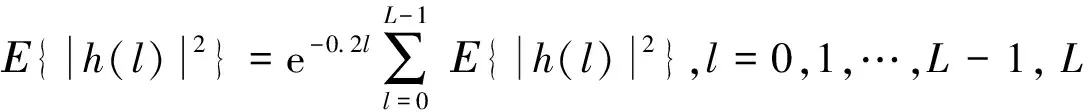
图5 a3取不同值时导频位置取值

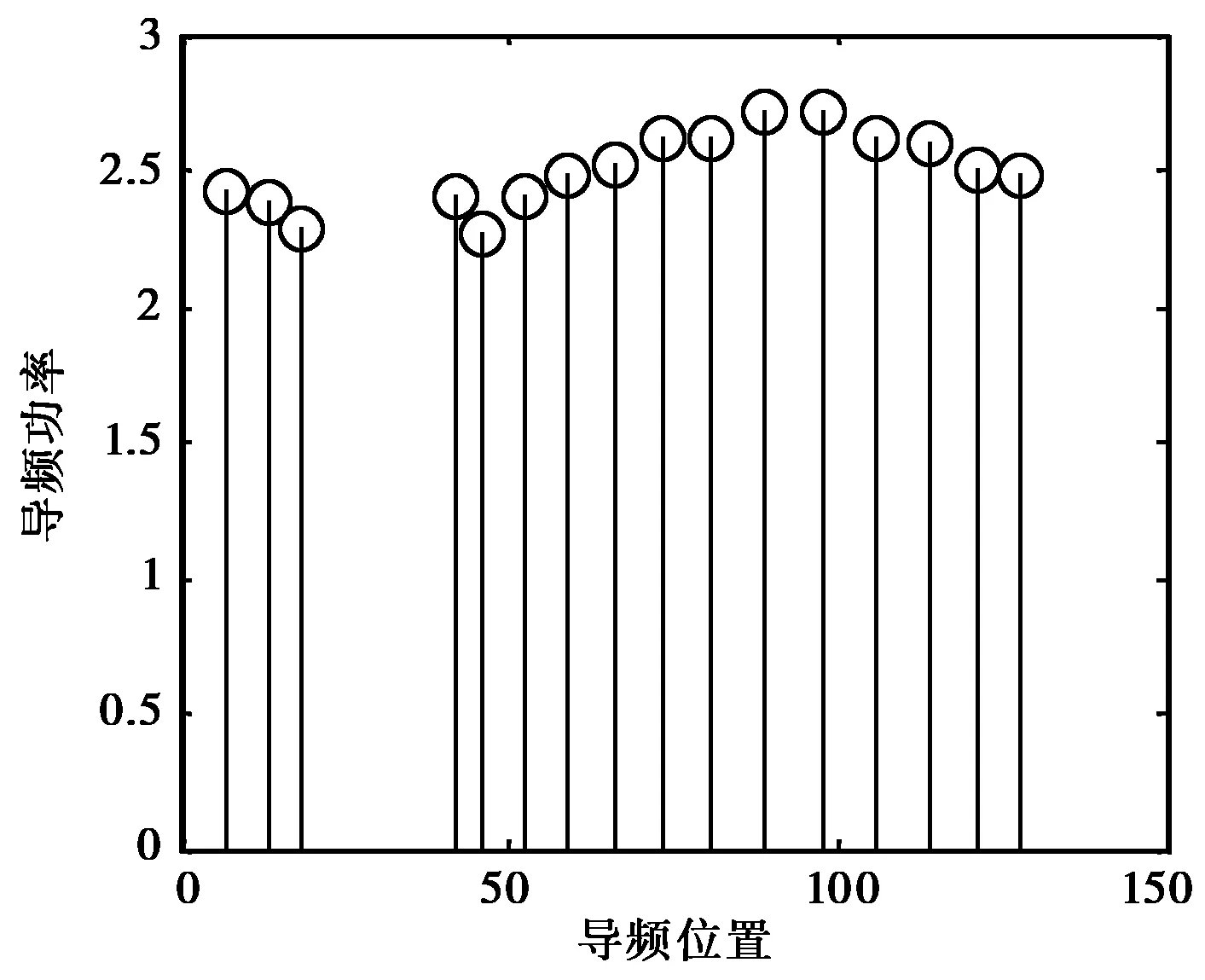
图6 最优导频位置及功率分布

两种认知无线电环境下四种导频设计方法的特点以及所设计的导频位置分别如下：

1) 部分等间距导频设计

部分等间距导频设计[13-14]在可用子载波频带上等间隔设计导频位置，导频间距d=Nc/(Np-1)，当L=Np=16时，导频位置为

κp=[18154148 5562 6976 8390 97104 111118 125]，

κp=[619 3245 5871 8497 158171 184197 210223 236249].

2) 移动导频设计

移动导频设计首先按照等间隔设计预设导频位置，然后把位于PU频带的导频子载波移动到与其最近的可用子载波位置，导频位置为

κp=[19171941 4957 6573 8189 97105 113121],

κp=[118 3552 6986 100157 171188 205222 239256].

3) 文献[9]次优导频设计

Hu die等利用MSE上界最小化代替MSE最小化，给出的次优导频位置为

κp=[311161941 4351 5967 7583 9199 107115 123],

κp=[824 4056 7282 88100 157168 174184 200216 232248].

4) 本文提出的导频设计方法

本文假设导频位置满足三次方函数关系，通过搜索最优的a3获得最优的导频位置为

κp=[713 1842 4652 5966 7381 8998 106114 121128],

κp=[823 3953 6779 9099 158166 177189 203217 233248].

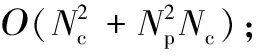
图7 非对称零子载波NC-OFDM系统导频设计MSE性能

图8 对称零子载波NC-OFDM系统导频设计MSE性能

4 结 论

本文研究了认知无线电NC-OFDM系统可用子载波非连续、非对称、非固定分布特性下的导频最优化设计问题.提出了一个围绕PU频带中心对称且满足三次函数关系的次优非均匀导频位置设计方法，推导了最优的导频功率分布.理论分析与仿真结果均表明：当可用频段非连续时，最优导频的位置和功率分布将呈现非均匀分布的特点，距离零载波越近，导频分布越密，导频功率越小；而且导频数的分布与非连续频段宽度并不是一种正比关系.本文给出的次优导频设计在保持良好的信道估计性能基础上，大大降低了导频位置搜索的计算复杂度.

[1] BUDIARJO I, RASHAD I, NIKOOKAR H. Efficient pilot pattern for OFDM-based cognitive radio channel estimation-Part 2[C]// 2007 14th IEEE Symposium on Communications and Vehicular Technology. Benelux, November 15, 2007: 1-5.

[2] RASHAD I, BUDIARJO I, NIKOOKAR H. Efficient pilot pattern for OFDM-based cognitive radio channel estimation-Part 1[C]// 2007 14th IEEE Symposium on Communications and Vehicular Technology. Benelux, November 15, 2007: 1-5.

[3] DONG Xuetao, XIE Xianzhong. Research on stochastic comb-pilot design for NC-OFDM system[C]// IEEE International Conference on Wireless Communications, Networking and Mobile Computing. Dalian, October 12-14, 2008: 1-3.

[4] GHOGHO M. On optimum pilot design for OFDM systems with virtual carriers[C/OL]// Proceeding of IEEE EURASIP International Symposium on Control, Communications, and Signal Processing, 2006[2012-11-01] http://www.eurasip.org/Proceedings/Ext/ISCCSP2006/defevent/papers/cr1227.pdf.

[5] 江 彬, 吴大焰, 高西奇. 基于遗传算法的 OFDM 系统导频设计[J]. 东南大学学报, 2008, 38(5): 746-751.

JIANG Bin, WU Dayan, GAO Xiqi. Genetic algorithm based pilot design for OFDM systems[J]. Journal of Southeast University, 2008, 38(5):746-751.(in Chinese)

[6] 胡 蝶, 何良华. 一种改进的MIMO OFDM系统导频设计方案[J]. 电子与信息学报, 2009, 31(4): 870-873.

HU Die, HE Lianghua. An improved approach of pilot design for MIMO OFDM systems[J]. Journal of Electronics & Information Technology, 2009, 31(4): 870-873. (in Chinese)

[7] HU Die, ZHOU Xiaolin. A new pilot design method for OFDM systems with virtual subcarriers[C]// IEEE International Conference on Wireless Communications, Networking and Information Security. Beijing, June 25-27, 2010: 73-77.

[8] BAXLEY R J, KLEIDER J E, ZHOU G T. Pilot design for OFDM with null edge subcarriers[J]. IEEE Transactions on Wireless Communications, 2009, 8(1): 396-405.

[9] HU Die, HE Lianghua, WANG Xiaodong. An efficient pilot design method for OFDM-based cognitive radio systems[J]. IEEE Transactions on Wireless Communications, 2011, 10(4): 1252-1258.

[10] 赵东峰, 刘 涛, 周贤伟. 滤波器组的多滤波器联合能量频谱感知算法[J]. 电波科学学报, 2009, 24(6):1146-1149.

ZHAO Dongfeng, LIU Tao, ZHOU Xianwei. Joint filter spectrum sensing algorithm using filter banks[J]. Chinese Journal of Radio Science, 2009, 24(6):1146-1149.(in Chinese)

[11] 赵东峰, 周贤伟, 程曾伟, 等. 采用最小最大准则的协作频谱感知融合[J]. 电波科学学报, 2011, 26(5): 923-926.

ZHAO Dongfeng, ZHOU Xianwei, CHENG Cengwei, et al. Combination based on the minimax rule for cooperative spectrum sensing[J]. Chinese Journal of Radio Science, 2011, 26(5): 923-926.(in Chinese)

[12] 李 莉, 黄立辉, 王 沛, 等. 一种基于多窗低复杂度的频谱检测算法[J]. 电波科学学报, 2011, 26(6):1083-1087.

LI Li, HUANG Lihui, WANG Pei, et al. A collaborative spectrum detection based on MTM with low complexity[J]. Chinese Journal of Radio Science, 2011, 26(6): 1083-1087.(in Chinese)

[13] SONG S, SINGER A C. Pilot-aided OFDM channel estimation in the presence of the guard band[J]. IEEE Transactions on communication, 2007, 55(8): 1459-1465.

[14] HUANG Q, GHOGHO M, FREEAR S. Pilot design for MIMO OFDM systems with virtual carriers[J]. IEEE Transactions on Signal Processing, 2009, 57(5): 2024-2029.