共存式频谱共享认知中继网络的中断性能研究

洪 浩 肖立民 张 焱，3 王 京

(1.清华大学电子工程系，北京 100084；2.清华信息科学与技术国家实验室，北京 100084；3.北京理工大学信息与电子学院，北京 100081)

引 言

认知无线电从诞生之日起，就受到了学术界的广泛关注[1].其核心是对频谱资源进行动态管理，在保证主用户通信质量的前提下，通过频谱共享，使次用户能够利用主用户的频谱进行通信[2].认知无线电能大幅度提高授权频谱的使用效率，但其缺点也很明显，即次用户由于功率限制往往很难获得较理想的通信质量[3].

将中继技术引入认知无线网络，是应对这一问题的有效举措[4].作为第四代(4G)无线通信的核心技术之一，中继技术通过"虚拟多天线"，使次用户接收端能获得额外的信道增益，提高通信质量[5].

认知中继网络结合了认知无线电与中继技术各自的优点，近年来逐渐成为研究的热点.中断概率是进行系统性能评估的最重要的参数之一，之前关于认知中继网络中断概率的研究已经取得了部分成果.在文献[6]中，作者对采用译码转发(decode-and-forward, DF)协议的认知中继网络的中断概率进行了分析，并得到了中断概率的理论下界；文献[7]给出了采用DF传输协议的认知中继网络中断概率的理论上界表达式；文献[8-9]在推导过程中，为了简化分析，将接收端的信噪比(signal-to-noise ratio, SNR)作为独立随机变量考虑.但是对一个共存式频谱共享网络，由于必须满足对主用户干扰功率的限制，因此，通过直传链路和中继链路在接收端分别获得的信噪比是非独立的，之前的分析方法变得不再适用.

本文分析了采用放大转发(amplify-and-forward，AF)传输协议的多中继认知无线网络的系统特性，分别推导了广播阶段和中继阶段中断概率的精确表达式.在广播阶段，研究了接收端信噪比非独立时的场景，得到了中断概率的准确闭式解.在此基础上，给出了多中继认知无线网络中断概率的理论下界.并通过数值仿真，验证了该理论分析.

1 系统模型

图1为一个多中继认知无线网络的系统模型.次用户网络(包括发送节点s、接收节点d和M个中继节点rl(1≤l≤M))可以利用主用户p的频谱进行通信.d除了能接收s通过直传链路发送来的信息外，还能通过中继链路，获得经由rl放大转发来的信息.本文假设网络中每个节点都采用单天线.一次完整的传输过程分为两个阶段：第一阶段，即广播阶段，s广播信息，d和所有的rl同时接收；第二阶段，即中继阶段，选择“最优”中继将信息放大转发到d.

图1 多中继认知无线网络系统模型

本文假设网络中的所有信道均为独立瑞利衰落信道.hij((i，j)∈{(s，d)，(s，rl)，(rl，d)})为从节点i到节点j的信道系数.噪声为加性高斯白噪声(Additive White Gauss Noise，AWGN).信道增益X=|hij|2服从参数为λij的指数分布，其概率密度函数(Probability Density Function，PDF)fX(x)=λije-λijx，∀x≥0.为保证主用户节点的服务质量，s和rl的发送功率必须满足

(1)

式中：Psd和Prld分别是s和rl的发送功率；Ith是主用户端预先设定的干扰门限功率.后文均考虑次用户采用最大发送功率，即

第一阶段，s向d和rl广播信息，d和rl的接收信号为

(2)

式中：xs是s的发送信号；nsd和nsrl表示从s分别到d和rl链路的AWGN，均服从N(0，σ2)分布.

第二阶段，从第一阶段所有未发生中断的中继节点中，选择一个“最优”的次用户中继节点rb将信息放大转发到d，有

(3)

最后，d将直传链路s-d和中继链路rb-d分别接收的信号采用最大比合并(Maximal Ratio Combining，MRC)进行合并.

2 中断性能分析

2.1 中断概率表达式

中断的定义：信息的传输速率R大于信道容量I[10]，即

(4)

式中：γ为接收端的信噪比，本文假设广播阶段与中继阶段信道带宽相同，信号为等时隙发送.

令As为所有在广播阶段未发生中断的中继节点组成的集合，有2M种可能.根据定义，如果第一阶段发生中断，即s和所有rl均发生中断的概率为

=Pr(γsd<γth，γsr1<γth，…，γsrM<γth)

=Pr(γsd<γth，As=φ).

(5)

(6)

这样选择的目的是为了使接收端的信噪比最大，最小化次用户的中断概率.在忽略时延的情况下，第二阶段发生中断的概率为

=Pr(γsd+γbest<γth，As≠φ).

(7)

前面对广播阶段和中继阶段的中断概率进行了分析，分别得到了其精确表达式.因此，采用AF传输协议的多中继认知网络的中断概率可以如下表示

(8)

2.2 中断概率下界

从式(8)可以看出，认知中继网络的中断概率由两个阶段各自的中断概率构成.

fX1，…，XM+1(x1，…，xM+1)=

(9)

则第一阶段的中断概率为

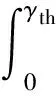
(10)

第二阶段，As≠φ，至少存在一个中继节点能成功放大转发信息.将式(7)作如下变形

Pr(γs d+γbest<γth，As≠φ)

(11)

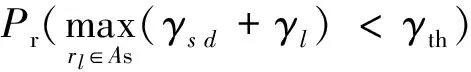
(12)

本文随后会通过仿真来验证这种近似的合理性.

因为γl≤γrld，可以将Pr(γs d+γl<γth)作进一步推导，有

Pr(γs d+γl<γth)≥Pr(γs d+γrld<γth).

(13)

根据文献[12]，γij的概率密度函数为

(14)

γij的累积分布函数(Cumulative Distribution Function，CDF)为

(15)

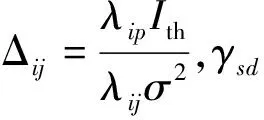
(16)

应用式(15)，集合As的概率为[3]

(17)

将式(16)和(17)代入式(11)，就得到了第二阶段的中断概率的下界

(18)

联立式(10)和式(18)，频谱共享模型下认知中继网络的中断概率下界为

(19)

3 仿真结果及分析

对不同中继数目(M=1，2，4)下的数值仿真结果与理论分析结果进行比较.仿真参数的设置如下[13]：传输速率R=1 bit/s/Hz；信道增益参数λsd=λsrl=λrld=1，λsp=λrlp=1；噪声功率σ2=0 dB.

从图2可以看出，论文理论分析得到的中断概率下界与仿真结果非常接近，这表明由式(12)通过近似带来的误差非常小.当M=1时，两条曲线几乎完全重合，随着数目M的增大，次用户中断概率迅速降低，但同时中断概率下界与仿真结果的差距逐渐增大，这是由于通过式(18)计算得到的下界误差逐渐累积变大.文中所提出的理论下界在中继数目较小时性能较好.在实际系统中，系统性能与开销存在折衷.对于一个认知中继网络，其中继数目通常不会太大[14]，因此，文中提出的理论下界是合理的.

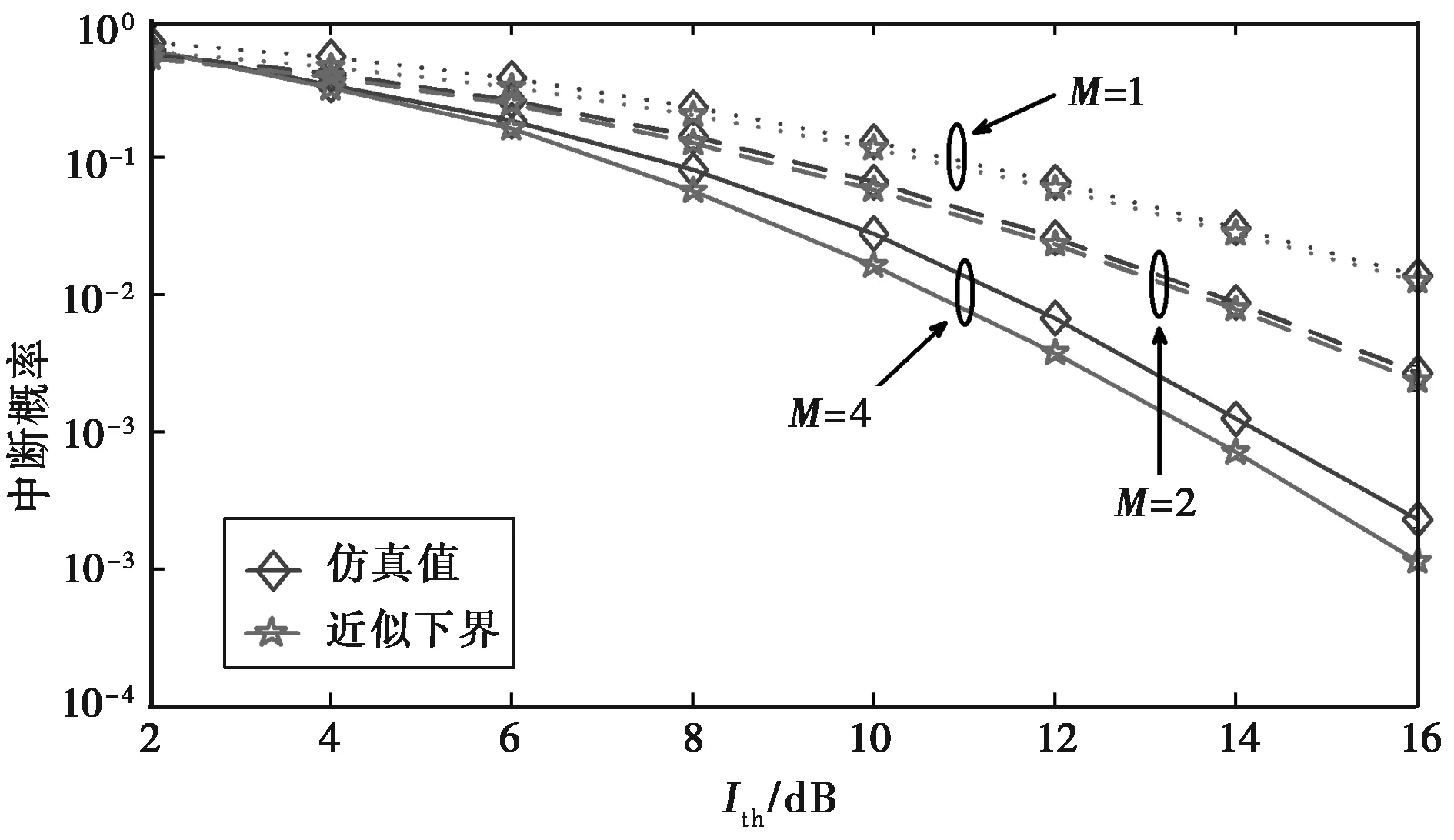
图2 M=1，2，4时的中断概率

从图2还可以看出，中断概率会随着主用户端干扰门限功率的增加而下降，这是由于次用户节点的发送功率增大而使系统的信道容量增大.另外，随着中继数目的增加，认知中继网络的分集增益也得到提升[15]，系统性能改善.

4 结 论

本文分析了在认知中继网络中，采用“选择-最优中继放大转发”传输协议的次用户系统的中断概率.推导了在广播阶段接收端信噪比非独立的情况下的联合概率密度.在此基础上，得到了多中继认知无线网络中断概率的理论下界.仿真结果证实了该理论分析的合理性，表明主用户的干扰门限功率越高，次用户的中断性能越好.另外，随着中继数目的增加，次用户网络能获得更高的分集增益.

[1] KIM Hyungjong, WANG Hano, LEE Jemin, et al. Outage probability of cognitive amplify-and-forward relay networks under interference constraints[C]// Proceedings of Asia-Pacific Conference on Communications(APCC). Auckland: IEEE, 2010: 373-376.

[2] ZOU Yulong, YAO Yudong, ZHENG Baoyu. Cooperative relay techniques for cognitive radio systems: spectrum sensing and secondary user transmissions[J]. IEEE Communications Magazine, 2012, 24(8): 98-103.

[3]BLETSAS A, SHIN H, WIN M Z. Cooperative communications with outage-optimal opportunistic relaying[J]. IEEE Transactions Wireless Communication, 2007, 6(9): 3450-3460.

[4] LEE K, YENER A. Outage performance of cognitive wireless relay networks[C]// Proceedings of IEEE Global Telecommunications Conference(GLOBECOM). San Francisco: IEEE, 2006: 1-5.

[5] LUO Liping, ZHANG Ping, ZHANG Guangchi, et al. Outage performance for cognitve relay networks with underlay spectrum sharing[J]. IEEE Communications Letters, 2011, 15(7): 710-712.

[6] 张 焱, 胡昕炜, 肖立民, 等. 基于多簇模型的自适应OFDM系统信道预测方法[J]. 电波科学学报, 2010, 25(6):1027-1033.

ZHANG Yan, HU Xinwei, XIAO Limin, et al. Adaptive OFDM channel predictor based on multi-cluster model[J]. Chinese Journal of Radio Science, 2010, 25(6): 1027-1033. (in Chinese)

[7] 唐菁敏, 冯思泉, 龙 华, 等. 基于中继选择的认知系统中继性能研究[J]. 昆明理工大学学报: 自然科学版, 2012, 37(2):39-42.

TANG Jingmin, FENG Siquan, LONG Hua, et al. Research on outage performance of cognitive-radio based on relay selection[J]. Journal of Kunming University of Science and Technology: Natural Science Edition, 2012, 37(2): 39-42. (in Chinese)

[8] MIETZNER J, LAMPE L, SCHOBER R. Performance analysis for a fully decentralised transmit power allocation scheme for relay-assisted cognitive-radio systems[C]// Proceedings of IEEE Global Telecommunication Conference(GLOBECOM). New Orleans: IEEE, 2008: 235-239.

[9] GUO Y, KANG G, ZHANG N, et al. Outage performance of relay-assisted cognitive-radio system under spectrum-sharing constraints[J]. Electronics Letters, 2010, 46(2): 182-183.

[10] CONTI A, WIN M Z, CHIANI M. On the inverse symbol-error probability for diversity reception[J]. IEEE Transactions Wireless Communication, 2003, 51(5): 753-756.

[11] ZOU Yulong, YAO Yudong, ZHENG Baoyu. A cooperative sensing based cognitive relay transmission scheme without a dedicated sensing relay channel in cognitive radio networks[J]. IEEE Transaction on Signal Processing, 2011, 59(2): 854-858.

[12] ALBERTO L. Probability and Random Processes for Electrical Engineering[M]. 2nd ed. New Jersey: Addison-Wesley Publishing Company, 1993.

[13] ZOU Y, YAO Y, ZHENG B. Cognitive transmissions with multiple relays in cognitive radio networks[J]. IEEE Trans on Wireless Communication, 2011, 10(2): 648-659.

[14] LANEMAN J N, WORNELL G W. Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks[J]. IEEE Transactions on Information Theory, 2003, 49(10): 2415-2425.

[15] 肖 亮, 庞文镇, 康 姗, 等. 机舱环境路径损耗和功率覆盖特征分析[J]. 电波科学学报, 2012, 27(1): 24-29.

XIAO Liang, PANG Wenzhen, KANG Shan, et al. Analysis characteristics of path loss and power coverage in cabin environment[J]. Chinese Journal of Radio Science, 2012, 27(1): 24-29. (in Chinese).