中药复方药物动力学总量统计矩法的实验验证研究
2013-04-22贺福元,邓凯文,刘文龙,石继连,伍勇,刘伟,贺庆平,李博
贺福元,邓凯文,刘文龙,石继连,伍勇,刘伟,贺庆平,李博

[摘要] 目的:对已建立的药物动力学总量统计矩法用补阳还五汤中黄芪甲苷、芍药苷、川芎嗪3个成分进行验证,建立中药复方多成分体系的药物动力学实验方法。方法:采用反相高效液相色谱法测定,其条件为C18色谱柱(4.6 mm×250 mm,5 μm);黄芪甲苷ELSD测定;流动相乙腈1%乙酸溶液(35∶65),流速1 mL·min-1;柱压 (15.0±0.408) MPa;温度30 ℃;芍药苷、川芎嗪的检测波长254 nm,流动相甲醇水(33∶67),流速1 mL·min-1;柱压(20.71±0.42) MPa。单个成分房室模型药物动力学参数采用DAS软件处理,总量统计矩按公式计算。结果:3个单成分在大鼠体内药物动力学都遵循二室模型(P<0.01),与叠加总浓度比,单个成分各参数相差最大上万倍,而总量统计矩参数的RSD为3.5%,3个成分药物动力学的总量统计矩参数AUCt (119.8±27.20) g·min·L-1;MRTt (210.0±54.49) min;VRTt (5.608±2.723)×104 min2;CLt为(0.319 6±0.068 8) mL·min-1·kg-1; Vt为(64.12±8.243) mL·kg-1; t0.95t为(588.9±149.4) min。这就说明3个成分总量的半衰期为(145.5±37.76) min,3药在0~674.2 min内代谢95%的浓度。结论:中药复方多成分药物动力学可采用总量统计矩法进行研究,该法能表征多成分体系总量的量时变化的动力学规律。
[关键词] 总量统计矩;药物动力学;谱动学;补阳还五汤;黄芪甲苷;芍药苷;川芎嗪
中药及复方药物动力学研究是阐明中药复方产生作用物质基础的关键问题,是阐明机体对中药及复方量时效关系的基础,也是中药复方制成控缓释制剂的理论基础[1]。由于中药复方为多成分体系,如按单成分药物动力学研究将会存在以下问题[25]:①怎样建立适宜多成分药物动力学研究的数学模型,并对参数进行测定;②在对照品缺少的情况下,中药复方多成分怎样进行药物动力学研究;③怎样建立宏观综合效应与总成分、单成分浓度对应关系。针对这些问题,作者前期创立了总量统计矩法,并有论文发表和成果获奖[6],但由于公式推导较复杂,参数的理论与实验测定问题没有深入阐明清楚,可能会影响同行在进行中药复方药物动力学研究时采用难度,为此,本论文先从第一个问题着手,详细阐明建模的思路及参数的意义及测定方法,再逐步报道其相关问题[7]。
补阳还五汤系清代王清任《医林改错》首载,该方由黄芪、当归、芍药、川芎、桃仁、红花、地龙组成,具有补气、通络的功能。在抗血栓、抗脑栓血、抗衰老、抗血脂及免疫功能方面都有广泛的作用[8]。本室对该方进行了大量的抗脑血栓作用机制研究,发现该方具有重要的抗血栓活性作用。其主要有效成分部位为总苷、总苷元、总生物碱和总多糖,其代表性成分为黄芪甲苷、芍药苷、川芎嗪等等,本文选这3个成分作为代表性成分来阐明中药复方多成分如何进行以总量统计矩数学模型为基础的药物动力学研究。
1 多成分药物动力学的建模数学思路
多成分的药物动力学研究是回答各成分浓度随时间量变规律,总体上有2种思路,一种是根据药物浓度具有叠加性,可将各单成分浓度直接相加构成总量药物浓度,然后再按单成分药物动力学方法进行参数求算,这种方法能获得总量药物动力学参数,但会丢失各成分的药物动力学参数,没有建立起总量药物动力学参数与单个成分药物动力学参数的关系;第二方法是进行函数曲线转换后再叠加处理,先将单成分药物动力学曲线转变成一种公用函数曲线,再进行曲线叠加,最常用的方法就是泰勒(Tatlor)转换叠加;傅利叶(Fourier)转换叠加等[9],但对转换后的叠加函数不能直接给有价的药物动力学参数,因此较宜采用统计矩转换叠加构成总量统计矩参数,与单成分统计矩参数一样,能表征多成分宏观的药物动力学行为。由于单成药物动力学的统计矩模型及参数已被熟悉,其总量统计矩参数也易为大家所接受,为此可以先将单成分的药物动力学统计矩化,亦正态分布曲线化,然后再进行叠加构成总量统计矩参数,亦总量正态分布曲线化,由此可得总量零、一、二阶矩参数。因此总量统计矩参数既能反映总量药物浓度的动力学行为,又能与单个成分的统计矩参数关联,可用于房室、非房室及不规则成分的药物动力学研究,是整合多成分药物动力学较宜的数学处理方法[6]。
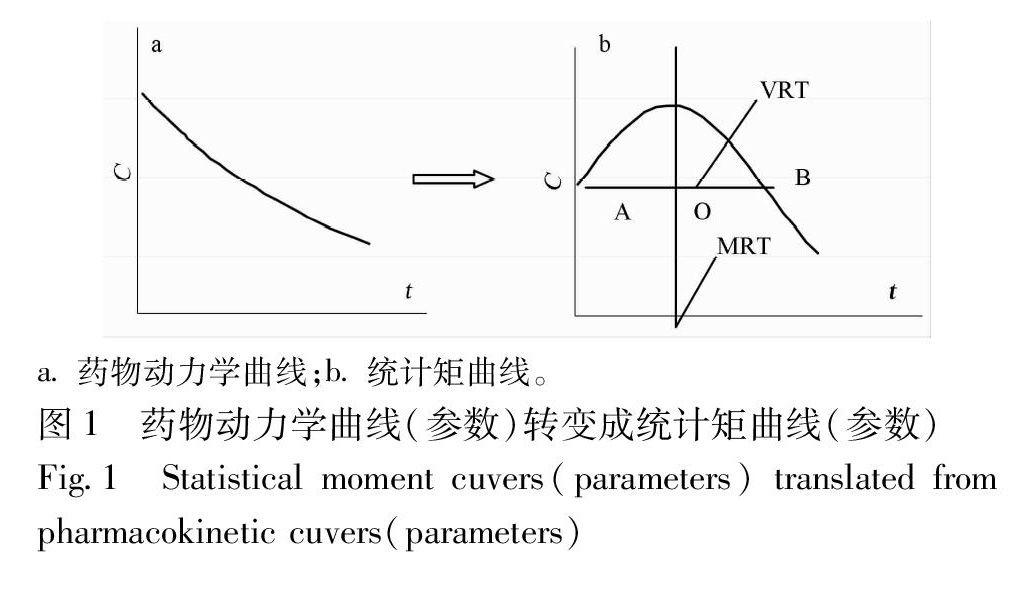
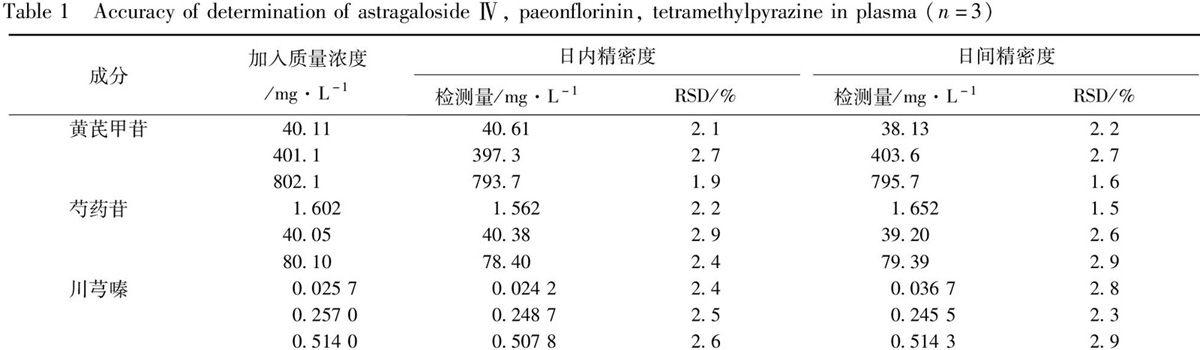
1.1 单成分的统计矩 将单成分的药物动力学曲线(参数)转变成统计矩曲线(参数)。其思路见图1。单成分药时曲线的统计矩化过程实际上就是将药物动力学曲线转变成正态分布曲线,其中重要参数有零阶矩(AUC)、一阶矩(MRT)和二阶矩(VRT)。
线性房室模型的统计矩参数:按统计矩原理可得到单成分零、一、二阶统计矩参数通式,为式(1),(2),(3)。
由上诸式可知:设Mi表示ri室模型第i项e的指数项前面的系数,αi表示第i项e的幂指系数。一、二、三室成分的各总量统计矩参数意义及计算参见文献[6]。非线性模型的统计矩参数:按统计矩原理可得到非线性单成分零、一、二阶统计矩参数通式,为式(5),(6),(7)。
各总量统计矩参数意义及计算参见文献[6]。
不规则模型的统计矩参数:按统计矩参数定义,用梯形法或抛物线法计算零阶矩(AUC),按文献的先计算AUMC(时间与曲线乘积下的面积),再计算MRT,再计算AUVC(时间平方与曲线乘积下的面积),再计算VRT[2]。
1.2 多成分体系的药动学总量统计矩参数的设定及与单个成分指标的关系 根据统计矩原理进行加合处理,见图2,图中a分别为2个成分的统计矩曲线,经统计矩原理加合计算后可得图中b的总量统计矩曲线,由此可得总量统计矩参数:总量零阶矩AUCt、总量一阶矩MRTt、总量二阶矩VRTt。假设中药复方为一个由n个单体成分群构成体系,其中m个成分服从线性药物动力学。第i个成分服从ri室模型。S1个成分服从非线性药物动力学。S2个为不规则模型,该中药复方成分总量的零阶矩、一阶矩、二阶矩及由此衍生的一系列动力学参数概念如下。
1.3 中药复方的总量统计矩参数 包括总量统计零、一、二阶矩以及由此衍生的其他总量统计矩参数。
总量零阶矩(AUCt):根据统计矩的加合性可计算中药复方多成分的总量统计矩,为下式(8)。
式中m表示线性成分的个数,ri 为第i成分代谢的室数,si为非线性成分的个数,si为产生多峰不规则成分个数。
总量一阶矩(MRTt):即为总量平均驻留时间,亦为各成分的总体均值,可定义如下式(9)。
总量二阶矩(VRTt):亦可采用相同方法处理,可得式(10)。
由上诸式可知,一个复方的总体药物动力学趋势由单个成分的动力学参数决定。其总量零阶矩等于各单成分的零价矩之和;总量一阶矩等于各单个成分一阶矩对零阶矩的算术平均值;总量二阶矩等于各单个成分的一阶矩的平方与二阶矩之和对零阶矩的算术平均值,再与总量一阶矩平方之差。这些性质是由总量统计矩的加合性决定的,亦有式(11),(12)。
式中MRT p1为1~i成分的总量一阶矩,VRT p1为为对应的总量二阶矩为;MRT p2为i~n成分的总量一阶矩,VRT p2为为对应的总量二阶矩。由总量零、一、二阶矩可衍生出其它总量药物动力学参数。
总量表观半衰期、清除率和表观分布容积:根据统计矩与半衰期有关系,中药复方多成分的总量表观半衰期为式(13)。
95%总量与累积95%总量浓度时间区间:由于中药复方为多成分体系,用零阶矩只表征其总成分的生物利用度,用一阶矩只表征诸成分平均驻留时间中心,这还不能完整表征多成分的药物动力学行为,因为平均驻留时间中心相同的一组成分其药物的种类与离散程度可以不同,也就是95%总量与累积95%时间区间不同,因此将一、二阶矩结合可表征95%总量浓度时间区间,亦为式(17)。
这样,式(8)~(19)构成了中药复方多成分药物动力学总量统计矩数学模型及参数体系[6,10]。
2 材料与方法
2.1 仪器与试药 Agilent1200液相色谱仪,Alltech 3300 ELSD检测与UV测定。瑞士Precisa公司的 20 A型电子天平;德国Heraeus公司的高速冷冻离心机及SZ1型快速混匀器。黄芪甲苷(批号110781200512)、芍药苷(批号110736200629)、川芎嗪(批号110817200305)(购于国家药品生物制品检定所),甲醇、乙腈为色谱纯,蒸馏水为二次重蒸馏水,其他试剂均为分析纯。其复方药材来源为:黄芪为豆科植物蒙古黄芪Astragalus membranaceus Bge.var. monghokicus (Bgo) Hsiao 干燥根;当归为伞形科植物当归Angelica sinensis (Oliv) Diels的干燥根;川芎为伞形科植物川芎Ligusticum chuanxiong Hort的干燥根;赤芍为毛莨科植物芍药Paeonia lactlora Pall的干燥根茎;桃仁为蔷薇科植物物桃Prunus persica (Linn) Batsch的干燥成熟种子;红花为菊科植物红花Carthamus tinctorius L.的干燥花;地龙为环节动物门钜蚓科动物参环毛蚓Pheretima aspergillum (Perrier)的干燥主体。处方黄芪60 g,当归9 g,川芎6 g 赤芍9 g,桃仁9 g, 红花9 g,地龙9 g。Wistar大白鼠,雌雄各半,体重220~300 g,由湖南中医药大学实验动物中心提供,许可证号SCXK(湘)20012004。
2.2 色谱条件 色谱柱Ultimate XBC18柱(4.6 mm×250 mm,5 μm),黄芪甲苷[11]采用Agilent 1200 Alltech 3300 ELSD测定,流动相乙腈1%乙酸溶液(35∶65),流速1 mL·min-1,柱压(15.0±0.408) MPa;温度30 ℃。芍药苷与川芎嗪采用Agilent UV测定,由于两者同时以指纹图谱的形式测定,可在原测定波长的基础上调整为254 nm[1213],流动相甲醇水(33∶67),流速1 mL·min-1,柱压(20.71±0.42) MPa;温度35 ℃。
2.3 给药与取血 将补阳还五汤水提醇沉制得的复方注射液(分别含黄芪甲苷2.160 g·L-1,芍药苷2.578 g·L-1、川芎嗪25.12 mg·L-1)。实验大鼠尾静脉给药2 mL,分别于给药后0.25,0.5,1.25,1.75,2.5,4.5,5.5,8,17.5 h,眼眶取血浆400 μL,并在1 h内进行样品预处理。
2.4 样品预处理 将补阳还五汤待测血浆400 μL置于尖底塑料刻度离心管中,加入三氯醋酸液1 mL,涡旋混合5 min,5 000 r·min-1离心10 min,取三氯醋酸层,常温下氮气流吹干,残渣用甲醇50 μL溶解,取20 μL进样。
2.5 空白血浆处理 于实验前,取大鼠血样按样品处理项下同法制得空白血浆样。
2.6 对照品液制备 精密称取黄芪甲苷对照品8.0 mg,用甲醇定容至10 mL,制得每1 mL含黄芪甲苷0.8 mg的对照品液;精密称取芍药苷对照品3.2 mg,用甲醇定容至10 mL,制得每1 mL含芍药苷0.32 mg的对照品液;精密称取川芎嗪对照品5.0 mg,用甲醇定容至100 mL,再稀释10倍制得每1 mL含川芎嗪0.005 mg的对照品液。
2.7 数据处理与分析 结果用DAS 2.0软处理,分别得单个成分、3成分叠加及平均的经典药物动力学参数,按自建的统计矩法分析得药物动力学总量统计矩参数。
3 结果
3.1 保留时间 黄芪甲苷:血样经预处理后,在黄芪甲苷色谱条件下进样测定,得血浆色谱图,见图3。大鼠血浆中黄芪甲苷峰在保留时间为15 min左右可完全分离。芍药苷与川芎嗪:在芍药苷、川芎嗪对照品液的色谱条件下测得芍药苷、川芎嗪的血浆色谱图。大鼠血浆补阳还五汤中芍药苷峰在保留时间为11.5 min左右,川芎嗪峰在保留时间为21.5 min左右可完全分离[2]。
3.2 标准曲线的制备及线性关系的考察 分别取试管6只,加入802.1 mg·L-1黄芪甲苷甲醇溶液对照品液10, 25, 50, 100, 200, 400 μL,水浴蒸干,再加入空白血浆400 μL,经样品预处理后,残渣用50 μL甲醇溶解,使血浆中黄芪甲苷的质量浓度分别为20.05~802.1 mg·L-1;另取试管6只,分别加入320.4 mg·L-1芍药苷甲醇溶液对照品液1,15,30,60,75,100 μL,水浴蒸干,再加空白血浆400 μL,经样品预处理后,残渣用50 μL甲醇溶解,使血浆中芍药苷的质量浓度分别为0.801~80.10 mg·L-1;又取试管6只,分别加入5.140 mg·L-1川芎嗪甲醇溶液对照品液2,5,10,15,20,40 μL,水浴蒸干,另加入空白血浆400 μL,经样品预处理后,残渣用50 μL甲醇溶解,使血浆中川芎嗪的质量浓度分别为25.70~514.0 μg·L-1。在前述色谱条件下进行测定,以黄芪甲苷浓度为纵坐标,黄芪甲苷峰面积为横坐标进行线性回归处理,得回归方程为C=0.183 2A-0.01,结果表明黄芪甲苷在20~800 mg·L-1呈良好线性(r=0.999 7),黄芪甲苷的最低检测浓度为0.6 mg·L-1 (S/N>3);以芍药苷面积为纵坐标,芍药苷浓度为横坐标进行线性回归处理,得回归方程为A=178.496 12C-3.361,结果表明芍药苷在0.80~80 mg·L-1呈良好线性(r=0.999 9),芍药苷的最低检测浓度为0.12 mg·L-1(S/N>3);以川芎嗪面积为纵坐标,川芎嗪浓度为横坐标进行线性回归处理,得回归方程为A=64.707 91C+86.325 75,结果表明川芎嗪在25.70~514.0 μg·L-1呈良好线性(r=0.999 7),川芎嗪的最低检测质量浓度为8 μg·L-1 (S/N>3)。
3.3 精密度和回收率精密度 按文献分低、中、高3个浓度进行日内和日间精密度、加样回收率试验研究。
精密度试验:取大鼠空白血浆400 μL,加入黄芪甲苷、芍药苷、川芎嗪对照品液,配制低、中、高3个浓度的样品,经预处理后分别测定日内精密度和日间精密度,结果见表1。
回收率试验:取空白血浆,加入一定量的黄芪甲苷、芍药苷、川芎嗪对照品液,分别配制高、中、低3个不同浓度的样品,经预处理后测定,按回归方程计算测得量,得到的平均方法回收率列为表2。由表1~2可知,本法能用于3个成分的药物动力学研究中的浓度测定。
3.4 药物动力学测定 取大鼠100只,随机分为10组,每组10只,每一组为一实验点,一组为空白。实验前夜禁食12 h,尾静脉给补阳还五汤注射液2 mL,定时取血与处理,可得药时曲线,见图4。结果用DAS 2.0软处理,分别得单个成分、3个成分叠加及平均的药物动力学参数,见表3,按自建的统计矩法分析得药物动力学总量统计矩参数,见表4。
3.5 补阳还五汤中黄芪甲苷、芍药苷、川芎嗪药物常规药物动力学及总量统计矩参数计算 先用DAS软件进行曲线拟合,得表3中常见的药物动力学参数,复方中黄芪甲苷、芍药苷、川芎嗪3个成分在大鼠体内药物动力学都遵循二室模型(P<0.01),再依式(1)~式(4)的计算公式对黄芪甲苷、芍药苷、川芎嗪单个成分的统计矩参数。如没有进行曲线拟合,也可直接用梯形法或抛物线法按有关统计矩公式进行计算,然后运用式(5)~式(11)将3药的决量统计矩进行加合计算得总量药物动力学统计矩参数,在计算过程一定要注意只有AUC(零阶矩)、AUMC(时间与曲线乘积下的面积)、AUVC(时间平方与曲线乘积下的面积)能进行相加,而MRT,VRT不能相加,只能按公式MRT=AUMC/AUC,VRT=AUVC/AUC-MRT2计算,其他参数在MRT参数基础上进行计算。用上法算得补阳还五汤中3个成分的统计矩参数列表4,其中总量统计矩参数AUCt为(119.8±27.20) g·min·L-1;MRTt为(210.0±54.49) min;VRTt为(5.608±2.723)×104 min2;t1/2为(145.5±37.76) min;CLt为(0.319 6±0.068 82) mL·min-1·kg-1;Vt为(64.12±8.243) mL·kg-1;t0.95t为(588.9± 149.4) min。
3.6 补阳还五汤中黄芪甲苷、芍药苷、川芎嗪3个成分95%总量浓度与累积95%总量浓度代谢时间区间 按式(14)计算得3药的95%总量浓度在[210.0-1.96(5.608×104)1/2,210.0+1.96(5.608×104)1/2] min,亦在-254.2~674.2 min时间内代谢95%的浓度。按式(16)算得t0.95t为588.9 min,故累积95%总量浓度代谢时间区间为[-∞,588.9] min。
3.7 补阳还五汤中黄芪甲苷、芍药苷、川芎嗪的药动学参数的比较 以3个成分叠加拟合而得的药物动力学参数(P<0.01)为标准对照组,表3中其他组与之的百分比值列于表5。
表3诸成分参数比较可采用等级资料的χ2检验,其χ2=279 8χ20.01(36)=58.619,说明诸成分参数差异显者(P<0.01),由表5可知,以川芎嗪的参数B的比值最小,为0.050%;以芍药苷的K10的比值最大,为2 883%,两者相差6万倍,黄芪甲苷、芍药苷、川芎嗪组的RSD分别为18.32%,172.4%,169.7%,这说明中药复方中各成分的药物动力学参数相差悬殊,彼此之间参数不能相互代替。平均组与叠加组的χ2=165.7χ20.01(9)=21.666,其RSD也为117.9%,远大于一般药物动力学实验误差5%,因此不能用各成分药物动力学参数的平均值来代表总量的药物动力学参数,也就是说总量的药物动力学参数不是各成分药物动力学参数的简单相加。
同理,以叠加成的3个成分统计矩参数为对照组,表4中其他的总量统计矩参数与之百分比值列于表6。
表4诸成分的统计矩参数的χ2=1 962χ20.01(25)=44.314,说明诸成分与方法的总量统计矩参数差异显著(P<0.01)。由表6可知,以川芎嗪的参数AUCt的比值最小,为0.054 6%;以芍药苷的CLt的比值最大,为1 080%,两者相差1.7万倍,黄芪甲苷、芍药苷、川芎嗪组的RSD分别为31.63%,174.2%,113.6%,这也说明中药复方中各成分的药物动力学总量统计矩参数相差悬殊,彼此参数之间不能相互代替。平均组与叠加组的χ2=212.3χ20.01(5)=15.086,其RSD也为108.3%,也大于一般药物动力学实验误差5%,因此也不能用各成分统计矩参数的平均值来代表总量统计矩参数,但按式(6)~(13)总量统计矩公式计算的各参数的RSD为3.510%,小于一般药物动力学实验误差5%,同时两者的χ2=1.006 1χ20.01(5)=15.086,因此只有按总量统计矩计算方法对各成分的统计矩参数进行加合计算,所得结果才能与成分叠加的总量的统计矩参数一致,也就是说本文所建立的式(1)~(13)的总量统计矩的数学模型能客观真实地反映各单个成分总量的药物动力学行为。
4 分析与讨论
4.1 中药及复方多成分药物动力学研究 中药及复方为多成分复杂体系,其产生的整体效应为诸有效成(辅助成分)在体内作用的综合表现。对于中药多成分的药物动力学研究目前仍采用单一成分的房室模型研究方法,这必然产生前述3个问题,其中最关键的问题是怎样表达多成分药物动力学的数学模型和多成分与效应的关联性问题[14],前文解决中药及复方药物动力学数学模型问题,本文采用实验进行验证。根据统计矩原理可知[4,15],统计矩为非房室模型,能表达线性房室、非线性MichaelisMenten和不规则曲线模型,能用已知曲线通过统计矩公式直接计算,也可通过各取血点用梯形法或抛物线法进行计算,故能用来表达中药及复方单成分与多成分药物动力学整体行为:由总量零、一、二阶矩及衍生的总体表观清除率、总体表观分布容积构成主要总量统计矩参数体系。由表5,6的对比数据可知,只有按总量统计矩方法对各成分的药物动力学参数进行加合计算,所得总量统计矩参数结果才能与诸成分叠加的总量的统计矩参数一致,才能反映多成分的整体浓度量变的动力学规律。
4.2 总量统计矩的特点 由统计矩原理和式(5)~(13)可知:总量统计矩具有2大特点[15]:①具加合性,单个成分经统计矩处能构成总量统计矩参数;反之,总量统计矩又能分解成单个成分统计矩;总量统计矩减去一部分成分总量统计矩会得另一部分总量统计矩,利用这一原理可进行血样空白干扰的消除;②具偶联性,能与多维变量曲线偶联,建立起多维曲线下的总量统计矩参数。如与HPLC指纹图谱与药动学偶联得保留时间、药物动力学代谢时间二维变量对药物浓度曲线总量统计矩参数;HPLC指纹图谱与效应偶联得保留时间、药物浓度(响应值)二维变量对药物效应曲线总量统计矩参数,前者称谱动学、后者称谱效学[1617],如HPLC指纹图谱与药动学、效应偶联得保留时间、药物动力学代谢时间、药物浓度(峰响应值)三维变量对效应曲线总量统计矩参数,称谱效动力学。因此,总量统计计矩可用于任何多成分变量的中心和离散性分析,是研究中药多成分体系动态量变、效应变化的有力的数学工具。
4.3 总量统计矩药物动力学模型使用时应注意的问题 由式(1)~式(11)的推导过程可知,总量统计矩药物动力学模型是建立在药物浓度化学动力学量变的模型的基础上,其适用性在于能用本模型表达体内各成分的浓度整体量变。不能简单地用本模型计算出来的总量来推断药物生物效应(药效与毒效)的大小,原因在于各成分的效应与毒效应系数不同,因此多成分的总量效应并不简单地与总浓度呈相关性,不能用单个成分的浓度相加来表达。总成分浓度量变统计矩参数与总效应统计矩参数并不重迭,只有将各成分的浓度量变乘上效应系数后,将浓度转化为效应后,才能用总量统计矩计算得出总效应的总效应统计矩参数,才能用来评价药物总效应,这时总量统计矩对单个成分效应的整合与对单个成分药物动力学整合一样,其总效应统计矩参数能指导临床用,这方而的详细阐明请读者参考相关文献[7]。中药多成的药物动力学与效应动力学不对应是有别于西药单一成分的药物动力学与药效动力学对应最为明显的地方。
本文详细阐明了中药复方多成分药物动力学总量统计矩数学模型的建立原理、实验与计算方法,适用于已知能测准的中药代表性成分,但中药绝大多数成分的没有对照品或为未知成分,因此怎样利用指纹图谱测定中药复方多成分技术,并与药物动力学关联构成的谱动学来测定中药复方表观药物动力学参数,亦谱动学参数将另文详述。
[参考文献]
[1] Loew D,Kaszhin .Approaching the problem of bioequivalence of herbal medicinal products[J]. Phytother Res,2002,16(8):705.
[2] 贺福元.中药复方药物动力学数学模型的建立及对补阳还五汤的研究[D]. 成都:成都中医药大学,2006:6.
[3] Ludbrook J. Statistical techniques for comparing measurers and method of measurement:a critical review[J].Clin Exp Pharmacol Physiol,2002,29(7):527.
[4] 魏树礼.生物药剂学与药物动力学[M]. 北京:北京医科大学&中国协和医科大学联合出版社,1997:1204.
[5] Vengpedersin .Noncoupartmentalybased pharmacokinetics modeling[J]. Adv Deliv Rev, 2001,48(2/3):265.
[6] 贺福元,罗杰英,邓凯文. 中药复方动力学数学模型总量统计矩法的研究[J]. 世界科学技术——中医药现代化,2006, 9(6):13.
[7] 贺福元,邓凯文,邹欢,等. 中药复方谱动学与谱效动力学差异性的研究[J]. 中国中药杂志,2011,36(2):136.
[8] 陈冬,杨洁红. 补阳还五汤抗脑缺血作用的研究进展[J].中华中医药学刊,2010,28(1): 72.
[9] 数学手册编写组.数学手册[M]. 8版.北京:高等教育出版社, 2000:219,531.
[10] 段晓鹏,贺福元,周晋,等.补阳还五汤指纹图谱加合性的研究[J]. 中国中药杂志,2011,36(23): 3247.
[11] 李晓亮,邵旭,牛海军,等. 高效液相色谱——蒸发光散射检测法测定补阳还五苷酮胶囊中黄芪甲苷的含量[J].安徽医药,2010,14(11):1286.
[12] 邓凯文,贺福元,刘文龙. RPHPLC法测定大鼠血浆中补阳还五汤及总苷中芍药苷的含量及药代动力学研究[J].中药材,2010,33(11):1768.
[13] 贺福元,刘文龙,贺庆平,等.反相高效液相色谱法测定大鼠血浆中补阳还五汤总生物碱中川芎嗪的含量及药代动力学研究[J].中国药物与临床,2005,5(12):920.
[14] 贺福元,罗杰英.中药复方药物动力学研究方法现状及研究方法探讨[J]. 中草药,2005,35(10):1582.
[15] 贺福元,周宏灏,邓凯文,等.指纹图谱的一种定性定量研究新方法:总量统计矩分析法[J].药学学报,2008,43(2):195.
[16] 贺福元,罗杰英,邓凯文,等.中药谱效学研究方法初探[J] 世界科学技术——中医药现代化,2004,6(6):44.
[17] 贺福元,邓凯文,刘文龙,等. 中药与人体的作用本质“网通虹势”的多重遗传谱效动力学[J].中国实验方剂学杂志,2011,17(2):240.
Experimental studies on pharmacokinetics of three components in
Buyanghuanwu injection on base of total quantum statistical moment
HE Fuyuan1, 2, 3*, DENG Kaiwen4, LIU Wenlong1, SHI Jilian1,
WU Yong1, LIU Wei1, HE Qingping1, LI Bo1
(1. Department of Pharmaceutics, Hunan University of Traditional Chinese Medicine, Changsha 410208, China;
2. Key laboratory of Property and Pharmacodynamics, State Administration of Traditional Chinese Medicine,
Changsha 410208, China; 3. Pharmaceutical Preparation Technology and Evaluation Laboratory of Traditional Chinese Medicine,
Hunan University of Tradition Chinese Medicine, Changsha 410208, China;
4. The First Affinity Hospital, Hunan University of Tradition Chinese Medicine, Changsha 410007, China)
[Abstract] Objective: To verify established the total quantum statistic moments model with astragaloside IV, paeoniflorin, tetramethylpyrazine in Buyanghuanwu injection, in order to establish a pharmacokinetic experimental method with multicomponent traditional Chinese medicine(TCM) compound system. Method: The RPHPLC was adopted, with the chromatographic column of C18, 4.6 mm×250 mm, 5 μm. As for astragaloside IV, the ELSD detector was adopted with acetonitrilewater(35∶65) as the mobile phase at 1 mL·min-1; the pressure of column was (15.0±0.408) MPa, the column temperature was 30 ℃. Regarding paeoniflorin and tetramethylpyrazine, the detection of wavelengths was 254 nm, with acetonitrilewater (35∶65) as the mobile phase at 1 mL·min-1, the column pressure of (15.17±0.41) MPa. The pharmacokinetic parameters for single component were dealt with DAS and the total quantum statistical moment(TQSM) parameters were calculated using formulations. Result: All of the three components followed the two compartmental pharkacokinetic model (P<0.01) in rats. Compared with the superimposed total concentration, each single component showed difference in parameters up to 10 000 times at most, whereas the RSD of TQSM parameters was 3.510%. The TQSM pharmacokinetic parameters of the three components in Buyanghuanwu injection showed that AUCt, MRTt, VRTt, CLt,Vt were (119.8±27.20) g·min·L-1, (210.0±54.49) min, (5.608±2.723)×104 min2, (0.319 6±0.068 8) mL·min-1·kg-1 and (64.12±8.243) mL·kg-1, respectively, suggesting that the halflife time for the three components were (145.5±37.76) min and 95% of them were metabolized within 0674.2 min. Conclusion: The TQSM can be used to study pharmacokinetic parameters of multicomponent TCM compound, because the method can characterize the pharmacokinetic regularity of quantumtime change in a multicomponent system.
[Key words] total quantum statistical moment; pharmacokinetics; pharmacokinetics with chromatographic fingerprint; Buyanghuanwu injection; astragaloside IV; paeoniflorin; tetramethylpyrazine
doi:10.4268/cjcmm20130222
[责任编辑 陈玲]
