科学哲学中的两种理论还原进路探析
2013-04-20智广元
智广元
(广州中医药大学 人文社科学院,广东 广州510006)
科学哲学研究的一个重要对象是科学理论及其关系,理论还原是科学哲学的一个重要论题。句法观与结构主义是科学哲学中的两大理论观:前者是以句法观为依托的理论还原进路,追求形式化与逻辑演绎,从美国科学哲学家欧内斯特·内格尔的经典还原模型到生物哲学家肯尼斯·斯盖夫奈尔的一般还原模型、一般还原取代模型,演绎精神逐渐弱化直至失败;后者是以结构主义为依托的理论还原进路,把科学理论看做由集合论谓词表达的公理化的、数学化的概念框架,所谓“理论还原”就是两个理论的数学框架同构。目前,后者是国际上探究理论还原问题的一条主要进路,而国内在该方面的研究相对较少。探析这两大理论观中的还原进路,将有助于理解科学理论及其结构和相互关系等问题。
一、句法观及其理论还原进路
按照逻辑经验主义的理解,科学理论是可以采用一阶语言表达的、部分在经验上得到解释的公理化演算系统。这样,理论就是语言学实体,由一阶语言的句法关系所决定,故而被称为理论的句法观或陈述观。从形式上看,一个演算就是一个三元组T= <L,→,A >。这里,L 是形式语言(语句的集合),A 是L 的递归子集(演算的公理),→是联系L语句的有限集合的递归演绎谓词。T 的定理是依据→从公理A 中推导出的L 语句。形式语言L 的理解I 是从L 到{0,1}的函数,这样,如果对于S 中的所有B,I(B)=1,并且S→T,那么对于T 中的所有B,I(B)=1。部分理解是I 的理解,I 是一个部分函数,即仅依赖L 的子集Dom(I)来定义。这样,科学理论的主体应该被看做部分得到理解的演算T = <L,→,A,I >。在这个意义上,公理相当于理论命题,部分演算与这些命题的经验基础或检验结果相关。
在理论的句法观理解中,关于还原论思想的最早论述见于美国逻辑实证主义的代表鲁道夫·卡尔纳普。1938 年,卡尔纳普在《统一科学的基础》中发展了“定律统一”的概念。所谓“定律统一”就是建构定律的同质系统。卡尔纳普认为,对于整个科学,一个学科的定律能够从另一个学科的定律中推导出来。20 年后,哲学家鲍尔·奥本海默与希拉里·普特南详细说明了这个概念,明确提出“把科学统一作为一个工作假说”,从4 个方面概括了还原论纲领的基本内容,强调理论的可推导性关系。内格尔意图弥补可推导性所存在的鸿沟,补充了可连接条件,并给出了这两个条件的形式化和“理论还原说”的最早、最清晰的定义,被称为“理论还原说”的经典模型——“还原是以一个(通常但不总是)对某个其他领域表述的理论来说明在一个研究领域中已经确立起来的一个理论或一组实验定律”[1]。该模型的形式化表达为:TB∧B∧A→TR,其中TB、TR分别表示还原理论与被还原理论,B 表示桥接原理,A 表示辅助假设(可有可无),→表示逻辑推导。
理论还原模型提出后,受到了诸多哲学家的批判。例如:美国科学哲学家费耶阿本德着重指出内格尔模型中的两个预设“逻辑演绎性”与“意义不变性”都不能满足,美国哲学家尼克斯认为内格尔还原模型太狭隘,英国科学哲学家菲利普·凯切尔以经典遗传学与分子遗传学的具体案例否认还原的可能性。为了解决这些困难,斯盖夫奈尔重新定义了还原,提出了理论的一般还原模型(GR)。[2]“斯盖夫奈尔提出的理论还原模型在讨论还原的文献中起到了重要作用。”[3]一般还原模型容许还原理论与被还原理论的修正,提出了“强类似”的非形式条件。如果与分别为TB、TR的修正版本,那么∧B∧A→,且TR与、TB与之间具有“强类似”关系。“斯盖夫奈尔修正了内格尔模型而保持了它的灵魂。”[4]斯盖夫奈尔的分析是一个“精致的内格尔式的框架”[3]。该模型被广泛采用,尤其是在生物学领域,声称抓住了孟德尔遗传学到分子遗传学的还原的本质。但是,当代生物学哲学的奠基人之一霍尔等人注意到孟德尔遗传学与分子遗传学之间存在着“多—多对应”关系以及“强类似”条件难以实现等问题。为了应对这些质疑,斯盖夫奈尔提出了更精致化的还原模型:一般“还原——取代”模型(GRR)。该模型形成一个连续统,完全还原与完全取代分别是这个连续统的两端。这样,该模型把保留了共同经验领域的理论取代也看做了理论还原,模糊了理论还原与理论取代的界限。这已与反还原论者的观点趋于一致,从而与内格尔建立理论还原模型的初衷相去甚远。例如,依照这种模型,氧化理论被还原为燃素理论。在化学史上,燃素理论流行100 多年,最后被证明燃素是不存在的,取而代之的氧化理论才是解释燃烧问题的正确理论。至此,这种理论还原进路已经走进了死胡同。
二、结构主义及其理论还原进路
“结构主义科学理论是在逻辑经验论的公认观点的困难无法解决的情况下兴起的。”[5]科学哲学中的结构主义学派是由威尔考克斯·阿当斯和帕特里克·苏佩斯开创,由约恝夫·史尼德、斯泰格缪勒、巴尔泽尔、穆林斯等人继承和发展的。依照结构主义的理解,理论具有集合论谓词表达的数学化结构,理论还原实质上就是使两个理论的结构同构。“同构定义只依赖于一个理论模型的集合论特征。”[6](P81)这种结构概念源于布尔巴基学派的“种结构”概念。如果A、A′都是非空集合,R、R′ 分别是A 与A′上的二元关系,称结构<A,R >与结构<A′,R′>同构,当且仅当,存在满足下述条件的函数f:(1)f 的定义域是A,f 的值域是A′;(2)f:A→A′ 是一一对应的函数;(3)对于A 中的任意x 与y,称xRy当且仅当f(x)R′f(y)。1950 年代,阿当斯把理论看做集合论实体,认为科学理论可以用一个对集来表示:T= <C,I >,其中C、I 均为有序n 元组,前者由所有满足集合论谓词的实体组成,称为理论的“特征集合”;后者由这些理论所应用的所有实体组成,称为理论的“预期理解”的集合。[7]这样,科学理论就失去了句法属性,等同于集合论谓词刻画的结构,所以,这种理论观被称为理论的“非陈述观”或“结构主义观”。“我将涉及……作为语句集合的理论概念,称之为理论的非陈述观”。[8]随后,苏佩斯建议在科学哲学中放弃使用形式语言。史尼德采纳了苏佩斯的建议,发展了阿当斯的定义集合论谓词的公理化方法,发展了这个理论的核心经验断言,于1971 年出版了《数学物理学的逻辑结构》一书,这标志着科学哲学中结构主义流派的出现。斯泰格缪勒进一步发展了史尼德的观点,着重发展了理论的动力学观点。1987 年,史尼德、巴尔泽尔、穆林斯三人合作出版了《科学的构造设计——经验知识局部和综合的结构》一书,“这本书被称为‘结构主义的纲要’”[9],标志着结构主义已经成为科学哲学中一个有极强竞争力的研究纲领;1996 年和2000 年,三人又合作出版了《科学的结构主义理论:核心问题与新的成果》和《结构知识的再现:范例》,发表了关于结构主义的一系列论文,此后结构主义日益丰富并不断发展。
从方法论上讲,库恩、拉卡托斯与劳丹一样,结构主义者的考虑对象不仅是单个理论,还包含理论演化以及由此形成的整个理论序列。最初,阿当斯用还原表达理论之间的关系,史尼德采用这个概念处理库恩的常规科学与科学革命的概念以及理论之间的关系。斯泰格缪勒沿用了这个提议,重点处理了发生科学革命的理论之间的关系。后来,巴尔泽尔、穆林斯与史尼德等人进一步阐述了理论还原问题。
我们首先来看阿当斯的理论还原模型。阿当斯在《刚体力学的公理化基础》(1955 年)和《刚体力学的基础与从粒子力学的定律中推演刚体力学的定律》(1959 年)两篇论文中讨论了理论还原问题。在分析热力学到统计力学的还原案例时,阿当斯依据他的理论观,提出了理论还原的形式条件,并认为这些条件适用于任何还原。如果T = <C,I >,T*= <C*,I*>,T 被还原到T*,用ρ 表示两者的还原关系,当且仅当:(1)如果i∈I,那么存在i*∈I*,使得iρi*;(2)如果c*∈C*且cρc*,那么iρi*。条件(1)被称为可连接性条件,如果基于关系ρ,T被还原到T*,那么对于T 中i 的任一预期理解,一定存在T*中i*的相应预期理解,使得i 与i*具有关系ρ;条件(2)被称为可推导性条件,如果实体c*满足与T*相关的集合论实体,并且c 与c*具有关系ρ,那么c 将满足与T 相关的集合论谓词。大致地,如果一个对象满足“理论T*的定律”,并且其他对象与这个对象具有关系ρ,那么其他对象也将满足“理论T 的定律”。(1)与(2)结合表明,所谓“理论还原”就是实现两个理论的同构,都具有<C,I >的结构形式;并且,如果T 被还原到T*,那么,若T*是正确的,则T 也是正确的。阿当斯把这个结论称为“正确性结果”,并把它看做“这是我们对还原的直觉要求”[10]。阿当斯的这些还原论述主要存在三个问题:一是许多还原的传统案例不满足阿当斯的还原分析,二是没有详细地考虑还原关系的“语义本质”,三是没有考虑不同的还原类型。第一个方面批评了阿当斯还原分析的核心,后两个方面批评了阿当斯还原分析的不完备性。例如:阿当斯的“正确性结论”难以成立,因为可推导性的要求太强。
1970 年代,史尼德与斯泰格缪勒发展了阿当斯的理论观,认为经验科学的最基本单位是理论元素,即T= <K,I >。其中,K 被称为“理论核心”,是一个纯粹形式化的数学结构,K= <Mp,Mpp,r,M,C >,这里Mp是T 的可能模型集;Mpp是T 的部分可能模型集;r 是一个“剔除”Mp中的理论内容得到Mpp的“限制函数”,即Mpp= r[Mp];M 是T 的模型集(M⊆Mp),C 是对于可能模型集Mp的约束;I 是理论的预期应用域,是不能完全形式化的部分。理论元素之间形成了复杂的理论网络进而构成整个科学理论体系。他们接受阿当斯的还原论述,并用来处理历时态的理论还原关系,包括库恩所称的“科学革命”。“(史尼德)从结构主义角度对科学理论重新进行形式化的研究,而且以此来处理历史学派的理论发展观。他试图将逻辑和历史,形式化和非形式化有机地结合起来。”[11]他们认为理论的发展就是旧理论不断发展,最终成为新理论的一部分。如果两个理论的理论元素之间存在着还原关系,当且仅当Mpp与M*pp存在着一与多的关系,使得T 的预期应用同T*的预期应用相关联,并且T 的预期应用包含在T*相关的预期应用之中。“斯泰格缪勒的还原概念源于阿当斯与史尼德的工作。依据这条进路,还原关系能够被看做匹配关系,通过它们的潜在模型之间的关系,联系两个理论的概念结构。”[12]但这种还原论述仍然存在着很多缺陷。艾耶尔批判了史尼德和斯泰格缪勒对还原的阐述,并对他们的这些定义作出了一些修改;而斯泰格缪勒和一些人断言:史尼德的论述应该被拓展,纳入较弱的近似还原的概念。这些批判意见都被考虑进了1980 年代的还原理论中。
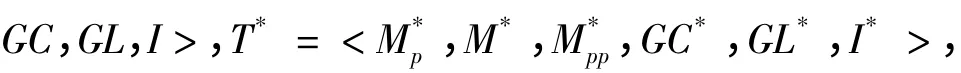
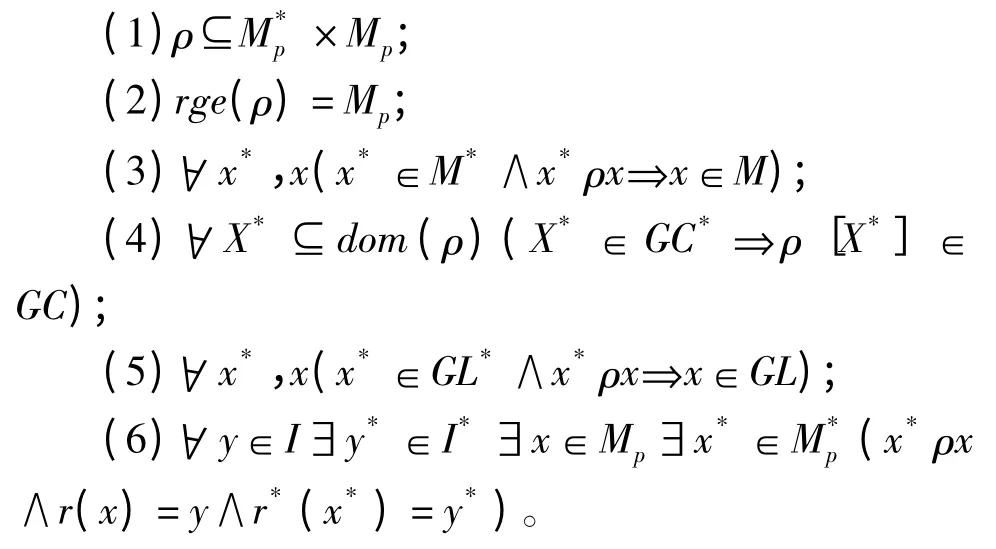
这样,“还原关系本身实质上是从被还原理论T的部分可能模型的集合Mpp的子集到还原理论T*的部分可能模型的一多对应(即函数变换)”[13]。与阿当斯的还原模型相比,这个还原模型中的理论元素M 与阿当斯定义中的C,公式(1)(4)分别与阿当斯模型中的(1)(2)大致相对应——虽然这一模型远比阿当斯的模型复杂。这个模型不仅考虑了理论的预期应用、理论的理想化因素,还考虑了理论的整体约束和整体联系等。
三、两种还原进路的对比
按句法观,科学理论的最基本特征是概念或陈述之间的逻辑关系——句法关系。按结构主义,科学理论最基本的特征是集合论谓词阐述的数学结构之间的关系。“从形式的观点来看,这条进路的本质是把集合论的公理增加到初等逻辑的框架内,然后,在这种集合论的框架内使科学理论公理化。”[6](P44)对比句法观与结构主义的理论还原进路,可以发现:
其一,理论观决定了理论还原观,理论的结构主义优于句法观。理论的句法观蕴含了两个预设:一是理论命题是通过假设——演绎方法来证明的,二是演绎推理具有形式化的特征。从卡尔纳普的“定律统一性”到内格尔理论还原模型以至斯盖夫奈尔的GR、GRR 模型,都追求逻辑演绎关系。“所有的理论,都能以一阶语言表述——有个很大的障碍。即使不是不可能,也存在着极大的困难。由此形成的纲领……误导了科学哲学很多年。”[14]结构主义的理论观或称非陈述观能够更精确地表达更多的理论——从数量上讲,它的使用范围非常广泛,适用于从所有的经验学科如物理学、化学经由生物学、神经生理学与心理学到社会学、经济学和行政学科等;从根本上讲,结构主义具有的非常明晰的概念框架,能够很精确地进行科学结构的表达。“这样精确化的表达方式,适用于这么广泛的范围,没有任何其他类似的方法可以与之相比拟。”[15]两者相比,结构主义理论观具有三个优点:首先,结构主义理论观采用集合论谓词表达理论及其关系,既能自然地排除库恩“常规科学”概念中的非理性因素,又能有效地刻画库恩的“科学革命”概念及其理论关系。“这实质上是下面的两个断言:(a)在陈述观中库恩被看成非理性的,而斯泰格缪勒的方法则没有这种含义;(b)陈述观中出现的问题(理论术语问题、先验因素问题与不可通约性问题等),在非陈述观中没有出现。”[16]其次,结构主义还原进路强调理论的结构不变性,能够对理论之间的关系作出更恰当的处理。所谓“理论同构”只是不同理论具有相同的数学结构即集合论谓词结构,而抽象的数学结构具有普适性,能够在理论转换时仍然保留下来。所以,结构主义还原进路避免了坚持拉卡托斯科学研究纲领理论的困难,而保留了它的思想精髓。再次,结构主义进路融合了理性因素和非理性因素,这就排除了陷入理性一元论与理性传统假定——只有单一的科学理性的源泉——的危险。“结构主义在当代科学哲学的研究中确立了形式化与非形式化、逻辑与历史相结合的方式,确实成为一个令人注目的研究纲领。”[17]
其二,两种理论还原进路经历了相似的发展过程。最初,两种理论还原模型的两个形式条件是相似的,都包括可连接性条件和可推导性条件,都强调可推导性,要求被还原理论与由还原理论导出的理论完全一致。“这是一个内格尔、阿当斯与史尼德所支持的基本的观念:被还原理论的定律能够从还原理论中推导出来。”[18]后来随着模型的发展,都容纳了还原理论与被还原理论的修正和近似。不同的是,句法观中的理论还原仍坚持追求共时态的逻辑演绎性,而结构主义理论观中的理论还原追求理论结构的不变性。
其三,结构主义还原进路包含了句法理论还原观的逻辑演绎性的优点,又容纳了它所不能包含的历时态的理论变化过程,具有更好的发展前景。“结构主义对当代科学哲学的重要贡献也许在于提出了用静态的形式化结构处理科学理论动态发展的思想。”[17]“结构主义者表达了还原在直觉上的必要条件(desiderata),在精神上它很接近于凯梅尼与奥本海默(1956),内格尔(1961)与亨普尔(1969)的经典还原论述。”[19]逻辑经验主义的还原进路包含了理论的修正、近似等而走向死胡同,而结构主义还原进路包含了上述内容且不断焕发出新的生机。穆林斯在1996 年提出了新的结构主义理论[9],把科学理论理解为7 元组,T= <Mp,M,Mpp,C,L,A,I >,其中Mp,M,Mpp的含义不变,C 表示约束的集合(联系同一个理论的不同模型的条件),L 表示联系的集合(联系不同理论的模型的条件),A 表示可容许的模糊的集合(不同模型之间能够接受的近似程度)。这样,科学理论模型就可能包含表达理论的模糊集合的模型之间的近似度。不仅如此,结构主义理论观还提出了科学理论的三层结构:理论元素、理论网络、理论整体子。理论网络表示由理论元素及其关系构成的整体,理论整体子表示由“本质性”关系使复杂的理论网络紧密结合在一起而形成的整体。这表明结构主义理论还原观还有很大的发展空间。
[1] [美]欧内斯特·内格尔. 科学的结构[M]. 徐向东,译.上海:上海译文出版社,2005:381.
[2] Kenneth F Schaffner.Reduction in Biology:Prospects and Problems[C]//Conceptual Issues of Evolutionary Biology. Cambridge/Massachusetts/ London/ Englanr:MIT Press,1984:429 -433.
[3] Rasmus Grønfeldt Winther. Schaffner’s Model of Theory Reduction:Critique and Reconstruction[J].Philosophy of Science,2009(4):119.
[4] Sahotra Sarkar.Genetics and Reductionism[M].New York:Cambridge University Press,1998:26.
[5] 张华夏.结构主义的科学理论观——兼评新经验主义[J].哲学分析,2010(2):140.
[6] [美]帕特里克·苏佩斯. 科学结构的表征与不变性[M].成素梅,译.上海:上海译文出版社,2011.
[7] Michael A Day.Adams on theoretical reduction[J].Erkenntnis,1985(23):161.
[8] Karl-Georg Niebergall.Structuralism,model theory and reduction[J].Synthese,2002(130):135.
[9] Walter de Gruyter.Book review:Structuralist theory of science,focal issues,new results[J]. Erkenntnis,1999(51):353.
[10] Adams E W. Axiomatic Foundations of Rigid Body Mechanics[D].Stanford:Stanford University,1955.
[11]张怡. 史尼德科学哲学思想初探[J]. 自然辩证法研究,1990(4):29.
[12]David Pearce.Stegmüller on Kuhn and Incommensurability[J].The British Journal for the Philosophy of Science,1982(4):389.
[13] Craig Dilworth. Scientific Progress:A Study Concerning the Nature of the Relation Between Successive Scientific Theories[M].Berlin:Springer Netherlands,2007:119.
[14] John Forge. Reflections on Structuralism and Scientific Explanation[J].Synthese,2002(130):109.
[15]Ulises Moulines C.Introduction:structralism as a program for modeling theoretical science[J]. Synthese,2002(130):1.
[16]Paul Feyerabend.Changing patterns of reconstruction[J].The British Journal for the Philosophy of Science,1977(4):351.
[17]张怡.一个引人注目的研究纲领——论科学哲学中的结构主义流派[J].自然辩证法通讯,1990(12):1.
[18]Dieter Mayr. Investigations of the concept of reductionⅡ[J].Erkenntnis,1981(16):109.
[19] David Pearce. Logical properties of the structuralist concept of reduction[J].Erkenntnis,1982(18):307.
