角反射器的线性非均匀电磁波散射特性

梁子长， 高 伟

（电磁散射重点实验室，上海200438）

0 引言

电磁波探测是获取物体信息的重要手段，由于电磁波探测具有穿透性、无需接触目标、可无损探测等优点，其在目标特征参数获取、隐藏目标探测等方面的应用日益广泛。但电磁波在自由空间中存在的形式很多，按波阵面分主要有平面波、柱面波及球面波等，而按波阵面上的电磁场幅度分布又可分为均匀电磁波及非均匀电磁波，其中线性变化非均匀电磁波较容易产生，是具代表性的非均匀电磁波，其特点是其中心位置的切向场为零，并向外线性增加。

按波阵面上电磁场变化方式，线性变化非均匀电磁波可分为一维和二维两种类型，这里主要介绍二维线性变化的类型。图1给出了二维线性非均匀电磁波的电场矢量分布示意图，包含旋转对称与轴对称两种主要切向场矢量分布形式，可认为其是两种新的极化形式，后续分别记为X和S。

图1 二维线性非均匀电磁波波阵面上电场矢量分布示意图

长期以来，尽管人们已经在远距离物体的跟踪、近距离物体的局部扫描探测等方面间接或部分涉及非均匀电磁波，但人们研究这类问题的依据及方法仍主要基于均匀电磁波理论［1～12］，即将非均匀电磁波简单地分为局部均匀电磁波，再按均匀电磁波理论进行研究；而对非均匀电磁波散射特性的研究十分少，仅文献［11］和［12］中提出近场电磁散射中对称极化的概念，即一种二维非均匀球面电磁波，但该研究认为，对称极化散射截面是随距离快速减小的量，未充分认识到这类非均匀电磁波在微波探测中的重要性。

本文主要在单位入射场条件给出目标非均匀电磁波散射截面的定义，指出其也可作为一种与观测距离无关的特征极化量，并采用矩量法仿真角反射器的线性非均匀电磁波散射问题，比较分析不同情况下角反射器目标的散射截面。

1 线性非均匀电磁波及散射特性

实际上线性非均匀电磁波是普遍存在的，典型如天线在其方向图凹点附近或快速变化区域辐射的电磁波，这里对偶极子天线方向图凹点附近辐射的电磁波进行分析［14］，假设某电偶极子沿Z轴放置，在其凹点所在的两极附近区域，其均匀电磁波项为零，若忽略3次及以上随观测距离衰减的高次项，则仅存在线性变化的非均匀电磁波项，即

式中：R 为观测距离；Il为电偶极子的电流矩；l为观测点至Z 轴的弧长；r、θ和φ 为以偶极子中心的球坐标系中的坐标方向矢量。可见，其区域电磁波的电场矢量E 呈轴对称分布，且其切向分量幅度大小与l成正比，即呈轴对称的线性非均匀球面电磁波，其在二维均呈线性变化。对应的，磁偶极在其两极区域辐射的电磁波即为旋转对称的线性非均匀球面电磁波。可见，对固定尺寸目标，入射的线性非均匀球面电磁波电磁场强度是随传播距离平方衰减的。

在此基础上，根据目前雷达散射截面的两个主要定义条件［13］，即单位入射场规定和距离衰减因子的分离，定义非均匀电磁波下物体的散射截面。根据这一定义方式，先规定线性非均匀电磁波的大小，由于线性非均匀电磁波在远场条件下存在均匀的径向分量，一般可取为该径向分量的幅度大小。对线性非均匀球面电磁波，根据能量守恒较易证明其大小将随距离平方衰减。在此基础上，定义物体对均匀或线性非均匀等不同电磁波的散射函数，这里记为χ，即

式中：Rs为观测点离物体中心的距离；E1i为物体所在位置入射的线性非均匀电磁波大小（含幅度和相位）；E1s为观测点处的散射线性非均匀电磁波大小；E0i为物体所在位置入射的均匀电磁波大小；E0s为观测点处的散射均匀电磁波大小。对应地，仍沿用雷达散射截面的概念，将均匀波与非均匀波下散射截面统一写为

为记述简便，这里以σpq表示不同极化组合下的雷达散射截 面，p、q 可 分 别 取v、h、s、x 四 种 极 化类型。

可见，研究非均匀电磁波下物体散射特性，在同一观测方向可获取的目标散射特征信息量将较大增加，在观测角度有限的情况下，这是十分有利的。

2 角反射器散射特性仿真

为分析非均匀电磁波散射特性，这里主要采用矩量法分别计算角反射器单双站及频率变化特性。

2.1 单站散射特性

假定二面角反射器的单面尺寸为0.4 m×0.1m，如图2所示，入射电磁波频率取为3GHz，采用矩量法比较计算角反射器目标在二维线性非均匀与均匀电磁波下散射特性。

图2 观测示意图

图3给出了角反射器目标在旋转对称二维线性非均匀电磁波（即x 极化电磁波）下散射特性，并与垂直极化RCS（即σvv）进行对比。

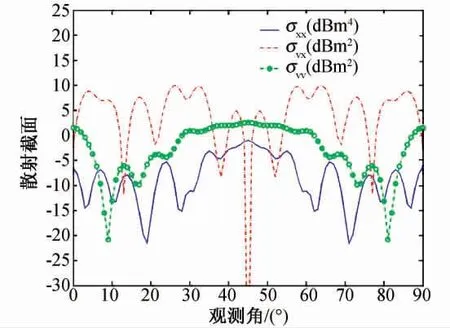
图3 角反射器的x极化后向散射特性

可见，非均匀电磁波下目标的后向RCS有较大不同，其中非均匀同极化散射截面σxx整体较小，但变化趋势与σvv较为一致；而非均匀交叉极化散射截面σvx整体较大，且变化趋势与σvv相反，即σvv较大时，σvx相对较小，反之亦然。

图4为角反射器目标在轴对称二维线性非均匀电磁波（即s极化电磁波）下的散射特性，并与水平极化RCS（即σhh）进行比较。与σhh相比，非均匀同极化σss与交叉极化σhs均整体较大，且变化趋势相反。

图4 角反射器的s极化后向散射特性

2.2 双站散射特性

这里仍选定图1所示的目标为观测对象，并假定入射电磁波方向平行于水平面，入射角取为45°，入射电磁波频率仍取为3GHz，分别计算四种极化电磁波照射下角反射器的双站散射特性。

图5给出了非均匀电磁波入射下角反射器水平面内的双站散射特性，由于该角反射器目标关于水平面对称，与垂直极化相关的交叉极化RCS均为零，这里不再给出。

图5 非均匀电磁波入射下角反射器的双站散射特性

可见，非均匀电磁波入射情况下，同极化RCS中σss比σxx大，这主要由于目标形状趋于放射型，而不是圆对称型；而与水平极化相关的两种交叉极化RCS较为类似。

图6给出了均匀电磁波入射下角反射器水平面内的双站散射特性。其中与非均匀电磁波相关的交叉极化RCS中，σsh远大于σsv，这主要因为水平面方向上角反射器目标的尺寸较大。

2.3 频率变化特性

图7给出了1GHz、2GHz和3GHz电磁波频率下角反射器目标的非均匀电磁波波后向散射截面。可见，其非均匀波同极化、交叉极化散射截面σss和σhs均整体随频率减小而减小，其中σss随频率的减小趋势更快。

图6 均匀电磁波入射下角反射器的双站散射特性

图7 不同频率下角反射器的非均匀波散射特性

3 结束语

本文按单位入射场条件给出目标二维线性非均匀电磁波散射截面的定义，指出其也可作为一种与观测距离无关的特征极化量，其研究可提供更多的目标信息量；并采用矩量法计算分析角反射器单双站，不同频率下非均匀电磁波同极化或交叉极化下散射截面特性，并与常规的垂直或水平极化RCS进行比较，表明其对目标特征探测的潜在优势。

［1］ Ouattara Y B，Mostarshedi S.Near-Field and Far-Field Models for Scattering Analysis of Buildings in Wireless Communications［J］.IEEE Transactions on Antennas and Propagation，2011，59（11）：4229-4238.

［2］ Jing Li，Xiang-jun Li.An Efficient Algorithm for Near-Field RCS of Electrically Large Dynamic Targets［J］.International Conference on Information Science and Technology（Nanjing），2011：26-28.

［3］ Ramin Deban，Halim Boutayeb.Deterministic Approach for Spatial Diversity Analysis of Radar Systems Using Near-Field Radar Cross Section of a Metallic Plate［J］.IEEE Transactions on Antennas and Propagation，2010，58（3）：908-916.

［4］ Christophe Bourlier，Philippe Pouliguen.Useful Analytical Formulae for Near-Field Monostatic Radar Cross Section Under the Physical Optics：Far-Field Criterion［J］.IEEE Transactions on Antennas and Propagation，2009，57（1）：205-214.

［5］ Arthur D Yaghjian.Planar Near-Field Measurement Techniques on High Performance Arrays.Part 1：Error Analysis for Nonscanning Beam Partterns，NBS［R］.AD-AO14397，1975.

［6］ W.charles symons，Keith W.Whites，Robert A.Lodder.Theoretical and Experimental Characterization of a Near-field Scanning Microwave（NSMM）［J］.IEEE Transcations on Microwave Theory and Techniques，2003，51（1）：91-99.

［7］ Frank Gumbmann， Phat Tran， Lorenz-Peter Schmidt.Sparse Linear Array Design for a Short Range Imaging Radar［C］.Proceeding of the 6th European Radar Conference，2009，（9）：176-179.

［8］ 张福顺，王胜，毛乃宏.用近场测量研究目标散射特性的一种新方法［J］.西安电子科技大学学报，1997，24（2）：217-220.

［9］ Pendry J B.Negtive Refraction Makesa Perfect lens［J］.Physical Review Letters，2000，85（18）：3966-3969.

［10］ Majid Ostadrahimi， Puyan Mojabi， Sima Noghanian.A Novel Microwave Tomography System Based on the Scattering Probe Technique［J］.IEEE Transcations on Instrumentation and Measurement，2012，61（2）：379-390.

［11］ 梁子长，岳慧，王晓冰，等.广义RCS及近场电磁散射建模应用［J］.上海航天，2011，28（2）：32-37.

［12］ 梁子长，李鸣，岳慧，等.高频区金属球定标体RCS的近场修正［J］.制导与引信，2012，33（3）：20-24.

［13］ Merrill I.S.，王军，等.雷达手册［M］.北京：电子工业出版社，2003.