渐开线齿轮加工过程中的大周期误差研究*
2013-04-16胡赤兵刘永平
□ 胡赤兵 □ 刘 浩 □ 刘永平
1.兰州理工大学 数字制造技术与应用省部共建教育部重点实验室 兰州 730050
2.兰州理工大学 机电工程学院 兰州 730050
传统的齿轮误差理论[1-5]中有一部分是对齿轮大、小周期误差的研究论述,从相关文献可知,以前的一些研究者把周期误差中齿轮在每一转的谐波次数K≤4称为大周期误差,而K>4称为小周期误差(或短周期误差)。大周期误差可以理解为由于几何偏心和运动偏心引起,本文着重介绍这两种偏心形式以及这两者间如何合成分离补偿与转化的。
齿轮加工方式主要包括滚齿加工和插齿加工,滚齿加工是一种非常具有竞争力的加工方法,它在精度和效率上都有很大的潜力;而插齿加工则在很早之前就已经投入了实际应用,由于滚齿和插齿在很多方面都是非常相似的,研究的时候可以相互借鉴。
1 滚齿加工大周期误差
1.1 几何偏心
几何偏心是在加工或者装配过程中齿轮的基圆中心相对其孔心的旋转轴不重合。如果假设两个旋转轴(机床心轴与齿轮内孔轴)之间的距离为e1,而且由此偏心加工的齿轮相对于心轴是满足的,而对于齿轮本身的内孔轴就不对了。几何偏心引起的左、右齿面啮合线误差计算可以参考图1计算。
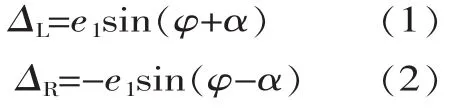
式中:若取ΔL方向为正,则ΔR的方向即为负。φ为齿轮转角,α为齿形角或压力角。
同时可得径向(Δr)、切向(Δt)上的齿廓误差为:
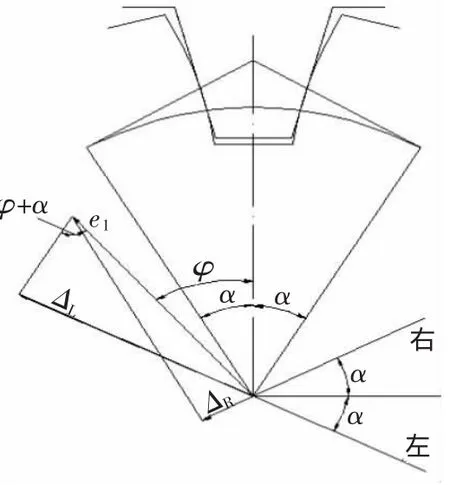
▲图1 几何偏心引起左右齿面啮合线误差
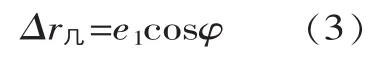

将这两个量分别投影到齿轮的左、右啮合线上:

由上可得到 ΔL=Δr几L+Δt几L和 ΔR=Δr几R+Δt几R,即左、右齿面啮合线误差等于该齿面上的径向与切向之和,进一步说明之前推导公式的可行性。
1.2 运动偏心
运动偏心是机床工作台和刀具之间运动的不协调所产生的齿轮一次谐波误差。而且机床的运动偏心也是产生齿廓线误差的重要因素,但是由安装偏心产生的几何误差引起的是齿廓径向误差,由机床运动偏心引起的则是齿廓的切向误差。滚齿加工中[2],滚切就相当于齿轮和齿条的啮合一样,但是存在机床运动偏心的时候就会使机床的工作台产生一个周期性的附加转动,进而使被切齿轮的回转不均匀,以不同的滚切速度滚切时的节点也会不一样,由于滚切的节点线速度不变,这时候回转速度的变化就产生了节点在某个方向的移动,另外这个滚切节点的位移在某些文献中被解释理解成齿廓瞬间切点所在的基圆的半径变化。如果把这种由机床运动偏心所引起的齿廓误差也认为存在偏心的话,这两种偏心之间还存在以下关系:

式中:e齿为齿轮的运动偏心 ;e机为机床的运动偏心;rb为被切齿轮基圆半径;rf为机床分度盘半径或分度蜗轮的半径;Δφ为机床的分度链误差一次谐波振幅的两倍,单位是弧度,它的半径是机床运动偏心e机。
运动偏心[3]的齿轮其左、右齿面相对于它的基圆都是正确的渐开线,但是相对于整个齿轮的旋转中心,会出现一定的误差。假如一个齿轮有运动偏心,它的左、右齿面的啮合增量可以参考几何偏心的算法,即:按照左、右齿面各自有一个大小一样,相位相差2α的几何偏心的齿轮进行计算。由图2可知:φL=φ-α,φR=φ+α。
由式(1)可得:
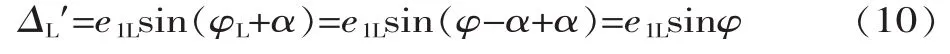
同理,由式(2)也可得:
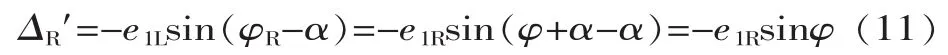
又因为e1L=e1R=e2故有:

式中:Δ′为运动偏心引起的左、右齿面的啮合增量;e1为几何偏心量;e2为被切齿的运动偏心量,其方向指向回转基准线,也就是工作台上角速度最小的地方;φ是齿轮转角。
运动偏心并不存在,实际存在的是左、右齿面的几何偏心e1L和e1R。所以需要用几何偏心来表示运动偏心,若运动偏心与几何偏心的夹角为θ,则式(12)改写成:

从式(13)看到,运动偏心对左、右齿面产生了一个大小相等且方向相反的正弦误差曲线。
1.3 几何偏心和运动偏心的合成与补偿
1.3.1 几何偏心和运动偏心在齿廓径向的合成
当有几何偏心和运动偏心时,将式(1)、式(2)代入Δ=ΔL+ΔR,则 Δ合=Δ+Δ′,式中 Δ合为几何偏心和运动偏心同时存在时的齿面啮合增量。
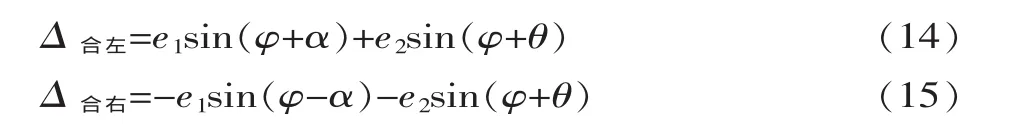
又从文献[1]可知,左、右齿面啮合线误差与径向误差的关系为:Δr=(Δ合左+Δ合右)/(2sinα), 将式(14)、(15)代入进行化简可得:

由式(16)可知,运动偏心e2对齿廓径向误差没有影响,几何偏心e1对齿廓径向误差才有影响,当φ=0时,存在最大径向齿廓误差。
1.3.2 几何偏心和运动偏心在公法线长度上的合成
如图2所示,左、右齿廓形成公法线长度偏差:
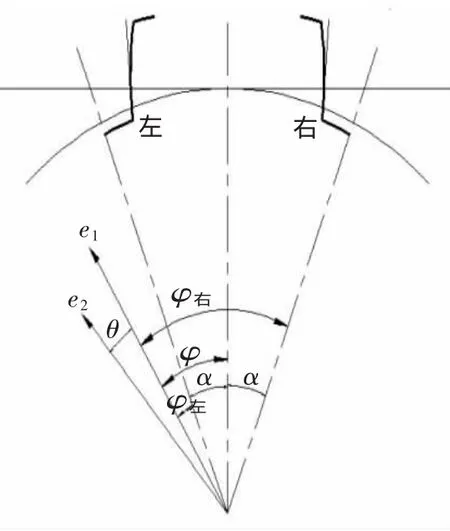
▲图2 几何偏心和运动偏心影响公法线

测量公法线时,必须将齿轮旋转,这样才可以跨齿测量,当齿轮逆时针旋转φ时,左齿面停在(φ-α),右齿面停在(φ+α)处,用(φ-α)代替式(14)中的 φ,用(φ+α)代替式(15)中的 φ,则有:

由式(18)可知,e1不影响公法线长度偏差,当φ+θ=0时,取得最小的公法线长度偏差,此时的e2指向最短公法线长度的中点。
1.3.3 几何偏心和运动偏心的补偿
由于几何偏心e1与运动偏心e2引起啮合线误差的周期相同,可以用一个整体误差的形式来表示几何偏心和运动偏心对左、右齿面啮合线的整体影响。总偏心可以用矢量合成法求得[2]:
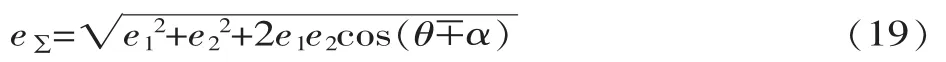
由总偏心所引起的左右齿面啮合线增量为:

式(20)中,左齿面取+,右齿面取-。
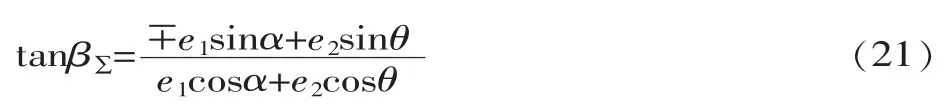
式中:β∑是总偏心对几何偏心的初相角,左齿面取-,右齿面取+。
根据运动偏心的大小与方向,引入一个几何偏心,使它与运动偏心的初相角θ=π,用来减小左右齿面运动偏心对其的影响。
设几何偏心 e1=ke2,代入式(19)得:
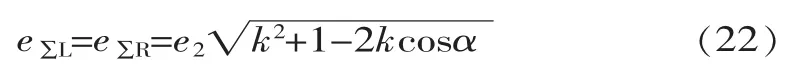
对 k 求导,并令其为零,可得:k-cosα=0,即k=cosα时取得极值,在工程中极值常等于最值,此时应为最小值。所以e1=e2cosα,代入式(22)得:
引入几何偏心且e1=e2cosα,补偿机床误差的(1-sinα),当 α=15°时,引入几何偏心 e1=e2cosα,此时有: e∑L=e∑R=0.26e2,补偿了机床误差的74%。通常齿坯安装成偏心和齿轮孔加工成偏心引入几何偏心。
2 插齿加工大周期误差
插齿加工的研究很多地方都可以参考滚齿,虽然工件系统误差与滚齿相同,但它们的刀具系统误差不同,一般从插齿刀偏心误差入手,研究插齿加工的大周期误差。
插齿刀[3,4]与被切齿轮以一定的传动比运动时,当加工的外齿轮从几何偏心的起始位置转过φ时,插齿刀转过-iφ(加工内齿轮时该数值为iφ),再将插齿刀的几何偏心e1d转化到齿轮上,e1d与回转基线的夹角就变成了-(iφ+θ),θ 是 e1d对 e1的初相角。
由图3可得e1d所产生的被切齿轮左、右齿面的啮合线误差为:

又因为e1d所产生的被切齿轮径向误差为:
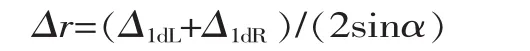
将式(23)、式(24)代入得:

当 iφ+θ=0 到 iφ+θ=π 区间时, 被切齿轮径向跳动ΔFr=e1dcos0-e1dcosπ=2e1d。
根据式(18)说明滚齿中公法线长度变动揭示的是运动偏心,但是不能揭示几何偏心的影响,同理在插齿过程中,也可以通过公法线长度的变动来间接地研究运动偏心。如图4,当齿轮往逆时针方向转过φ时,左齿面变成(φ-α),右齿面变成(φ+α),再把式 (23)、(24)中的 φ 分别令为(φ-α)和(φ+α),可得到:
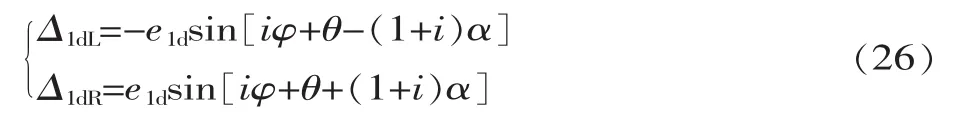
所以e1d产生的公法线长度偏差为:Δ公法=Δ1dL+Δ1dR=2e1dsin(1+i)αcos(iφ+θ),分别取 iφ+θ=0 和 iφ+θ=π,然后再相减可得公法线长度的最大变动为:
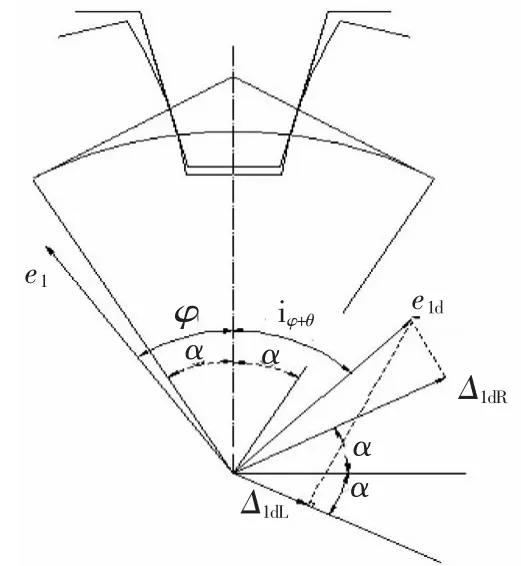
▲图3 插齿刀几何偏心引起啮合线误差
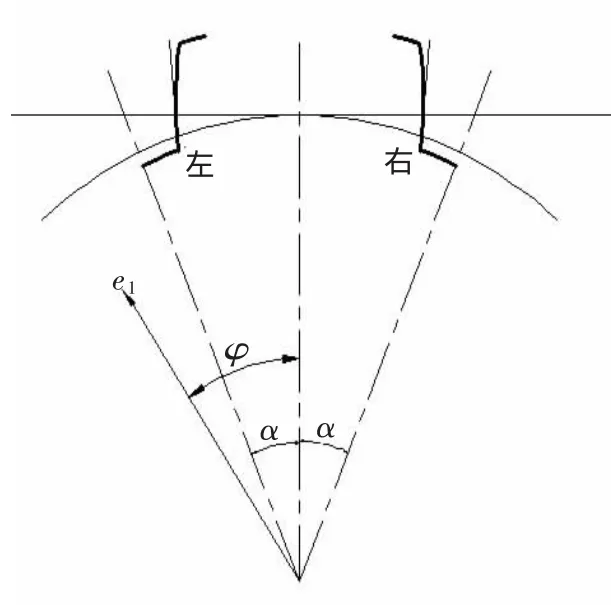
▲图4 公法线的变动

3 结论
1)对于滚齿加工来说,几何偏心对左、右齿面产生的啮合线误差等于该齿面上的径向与切向之和;
2)运动偏心对左、右齿面产生了一个大小相等且方向相反的误差且误差曲线是正弦曲线;
3)运动偏心对齿廓径向误差没有影响,几何偏心对齿廓径向误差才有影响。几何偏心不影响公法线长度偏差,可以通过引入几何偏心来抵消部分运动偏心引起的误差和补偿机床误差。
4)本文针对的是渐开线齿轮,但非圆齿轮节曲线的曲率中心与旋转中心不重合且非圆齿轮的半径在变化,使非圆齿轮的公法线很难测量,所以研究的下一步可以是参考相关文献[6-8],使用合适的方法对非圆齿轮进行研究。
[1] 刘继胜,罗姜.齿轮加工常见误差问题分析[J].机床与液压,2009(8).
[2] 王明侗.渐开线齿轮精度 [M].北京:机械工业出版社,1983.
[3] 柏永新.齿轮精度与综合检验[M].上海:上海科学技术出版社,1986.
[4] 经以广.圆柱齿轮加工误差机理、诊断及消减[M].沈阳:沈阳出版社,1991.
[5] F.L.Litvin.Gear geometry and applied theory [M].Nueva York:Prentice Hall,1994.
[6] 李福生.非圆齿轮[M].北京:机械工业出版社,1975.
[7] 胡赤兵,姚运萍,邬再新.非圆齿轮滚切加工运动控制模型[J].制造技术与机床,1999(9).
[8] 严慧萍,胡赤兵,刘立美.直齿非圆齿轮滚齿加工误差的研究分析[J].机械传动,2007(4).
