基于平面运动轨迹的间谐波参数计算方法
2013-04-16汤琳冯宇吴鹏飞
汤琳,冯宇,吴鹏飞
(1.武汉理工大学华夏学院,武汉 430074;2.中国电力科学研究院高电压研究所,武汉 430074;3.中国科学院大学电工研究所,北京 100190)
随着大量变频调速装置、工业电弧炉、风力发电机组等非严格工频周期性负荷接入电网,电力系统中的间谐波问题日益突出[1],其直接危害在于:100Hz以内的间谐波会引发电压波动与闪变,100 Hz~800 Hz之间的间谐波会影响无源滤波装置(并联电容器)的安全运行,对电力载波通信、电力控制和保护信号产生干扰。在此背景下,对间谐波进行准确、可靠的测量与分析具有重要意义。
目前,学者们提出了多种间谐波分析方法:傅里叶分析方法[2~3]通过提取信号频谱以反映分析时段上的整体信息,但无法反映局部特性,且需以同步采样和整周期采样为前提,前者可通过锁相技术实现,但后者则需要已知含间谐波分量的信号周期,这一点比较困难;小波分析[4]可反映信号局部特征,将其用于间谐波分析需解决的问题包括运算量较大、频带划分、小波基选取等;S变换[5]是一种可逆的局部时频分析方法,伴随着频率分辨率的提高,其运算量会非常巨大;支持向量机回归法[6]用于谐波分析时,需要很多如谐波信号频率等先验知识,且该方法计算代价高、分辨率较低、仍存在频谱泄露现象;自回归AR(autoregression)模型[7~8]需要提前知道谐波分量的数目,当模型的阶数取值较高时会发生谱线分裂现象,并且噪声会导致频谱偏移;Prony方法[9]将原始信号用一组复指数函数的线性组合来表示,其中信号阶数的确定是需要解决的重要问题,此外该方法的计算量较大;子空间分解算法[10]可以有效地克服噪声影响并具有超分辨率,不足之处是计算量大;奇异值分解SVD(singular value decomposition)方法[11~12]直接对采样数据构成的矩阵进行运算,在最小二乘法原理基础上隐含对窗外数据的外推,具有很高的频率分辨率,但该方法的计算量较大;智能参数估计方法[13~14]多与其他算法相结合,但都需要很多先验信息,且模型的学习时间也很长。
在现行的间谐波国标中[15],推荐使用离散傅里叶分析算法。为了实现对间谐波的准确分析与测量,必须进行整周期采样,因此必须首先确定含间谐波分量的信号的周期。为了解决这一问题,本文在文献[16~17]研究成果的基础上,提出了基于二维平面运动轨迹的含间谐波分量的信号周期及间谐波分量的幅值等主要参数的计算方法。仿真结果验证了所提方法的有效性。所提方法也可应用于其他需要获得周期信息的间谐波分析方法中。
1 基于图形模式识别的电能质量分析方法
文献[16~17]提出了基于图形模式识别的电能质量分析方法,其主要思想为:将三相或单相电压经αβ变换后得到两相电压,该两相电压在一个周期内的数据点在αβ坐标系下的合成曲线为一闭合曲线。此闭合曲线与“圆”的接近程度可以反映原三相或单相电压与理想电量的接近程度。
含有间谐波分量的电压信号可表示为

式中:U1是电压基波信号的幅值;UIh是间谐波分量的幅值;Ih是大于零的非整数;φ是初相角。此时电压信号的周期为基波信号周期与间谐波分量周期的最小公倍数。如果求出UIh和Ih(或u(ωt)的周期),就可以掌握间谐波的变化规律。
令uα(ωt)=u(ωt),将α相电压延迟0.25个工频周期得到β相电压为
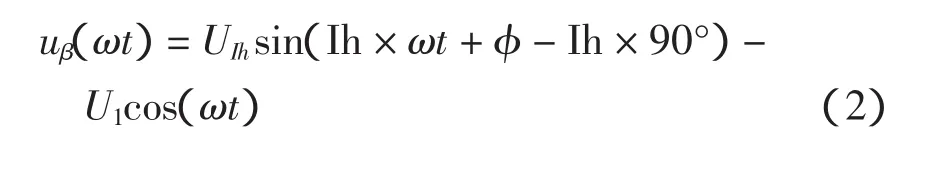
Ih=0.5时的含间谐波分量的电压信号如图1所示(U1=100、UIh=15,φ=π/12),此时u(ωt)的周期为40ms。在图1(a)中(100~120)ms和(120~140)ms两个时段里存在两个不同的交流波形,所以图1(b)中有两个不同的圆环。若Ih变化,则在u(ωt)的一个周期内的交流波形数等于合成曲线图形的圆环数。
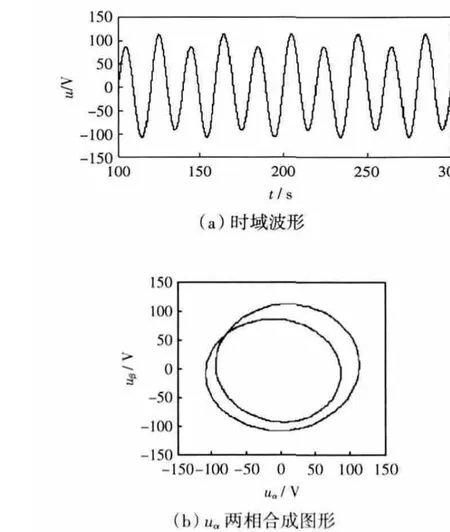
图1 u(ωt)(Ih=0.5)Fig.1 u(ωt)(Ih=0.5)
Ih=0.3时的含间谐波分量的电压信号及其r(ωt)如图2所示(U1=100、UIh=15,φ=π/12)。
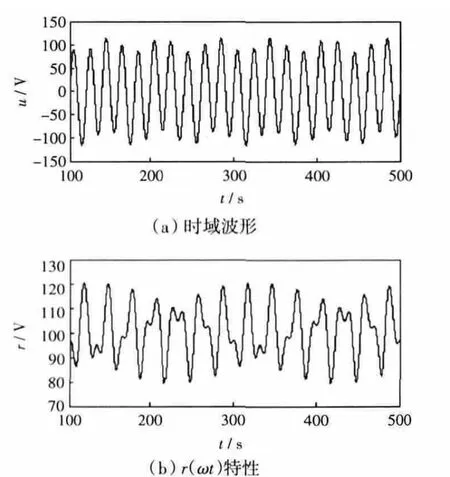
图2 u(ωt)(Ih=0.3)Fig.2 u(ωt)(Ih=0.3)
式(2)的αβ变换的合成曲线模长平方特性为
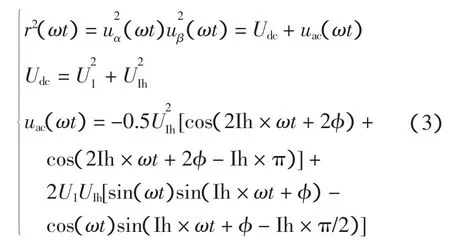
分析可知,r2(ωt)特性由直流分量Udc和交流分量uac(ωt)组成,uac(ωt)具有周期性,与Ih有关。
2 基于二维平面运动轨迹的间谐波主要参数计算方法
通过合成曲线在αβ二维平面的运动轨迹以及r2(ωt)特性可以求得u(ωt)的周期。
大量的仿真结果表明,r2(ωt)周期与u(ωt)的周期在很多情况下相等,当两者不相等时u(ωt)的周期为r2(ωt)周期的整数倍。因此在利用r2(ωt)特性的极大值点计算出其周期后,还要进一步确定它是否等于u(ωt)的周期。如第1节所述,在u(ωt)的一个周期内的交流波形数等于合成曲线的圆环数。因此对于合成曲线上的任意一点来说,只有经过一个u(ωt)周期的时间之后,合成曲线的运动轨迹才会再次经过该点。所以,只有当r2(ωt)特性的两个极值点所对应的u(ωt)合成曲线的αβ坐标均相等时,u(ωt)才经过一个周期。
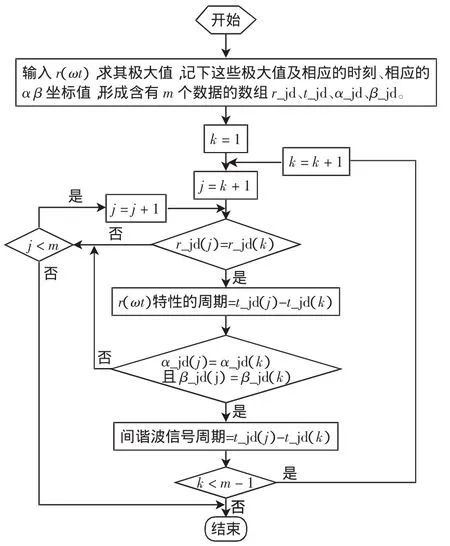
图3 求周期的算法流程Fig.3 Flow chartof periodicity
根据以上分析可得求取u(ωt)周期的算法流程如图3所示。其中,求r(ωt)极大值的方法是:在第q个采样点,比较r(ωtq-1)、r(ωtq)和r(ωtq+1)的大小关系。如果满足r(ωtq-1)
在确定了u(ωt)周期之后,由式(3)可知,在r2(ωt)的一个周期内对r2(ωt)进行积分求得Udc后,当U1已知时,就可以求出UIh为

3 仿真算例验证
通过仿真算例验证所提方法的正确性与有效性,令U1=100、UIh=15,φ=π/12,变化Ih,求取r2(ωt)周期、u(ωt)周期及UIh。计算结果如表1所示。从中可以看出,r2(ωt)周期、u(ωt)周期的计算值均与理论值相等,UIh的计算值与理论值十分接近。可见本文所提算法正确有效。
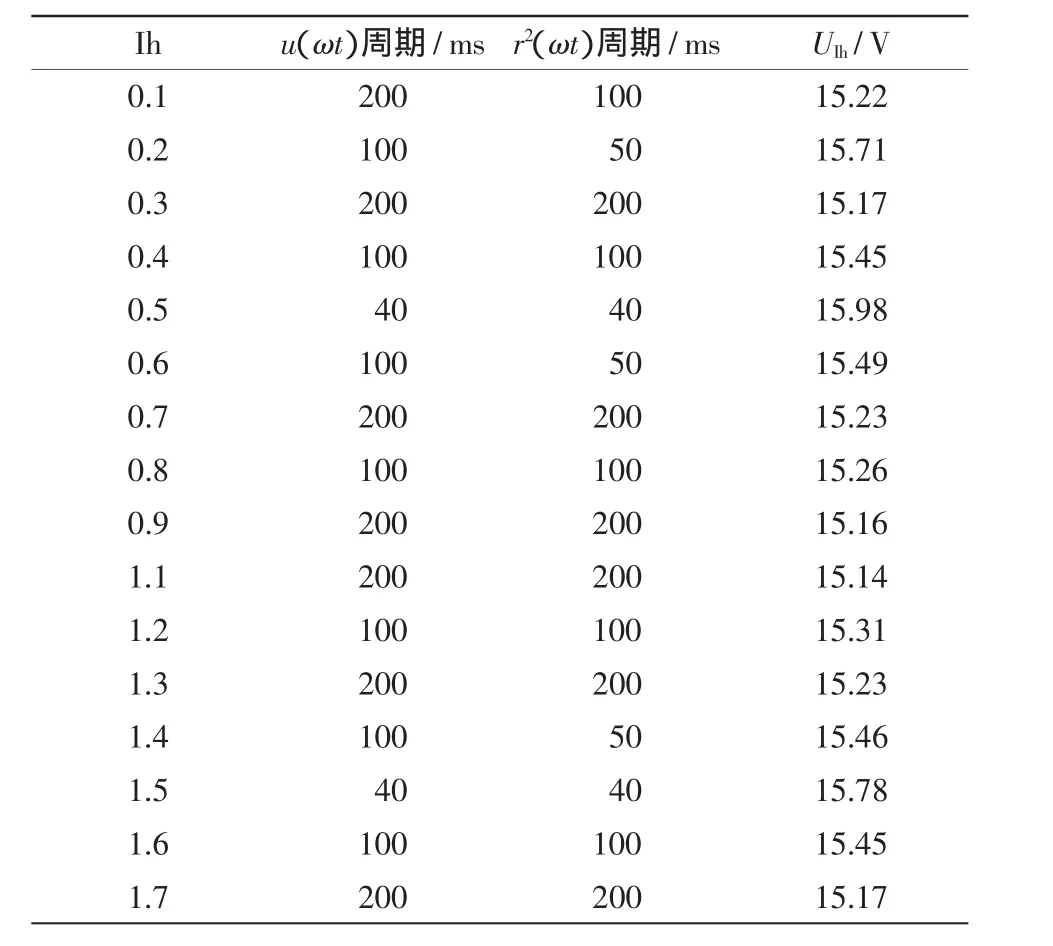
表1 u(ωt)周期、r2(ωt)周期及U Ih的计算值Tab.1 Calculation resultsof u(ωt)periodicity,r2(ωt)periodicity and U Ih
4 结论
(1)提出了通过含有间谐波的电压信号在αβ平面的运动轨迹与其合成曲线模长平方特性相结合的电压信号周期计算方法及间谐波分量幅值的计算方法。
(2)对Ih=0.1~1.7的u(ωt)的仿真计算结果表明,所提方法正确有效。
(3)αβ合成曲线模长平方特性r2(ωt)的极值求取,需要考虑噪声的影响,对噪声的预处理技术将作为本文今后的重要研究方向。
[1]张红瑛,滕召胜,温和,等(Zhang Hongying,Teng Zhaosheng,Wen He,et al).九点变换改进FFT高精度谐波分析方法(Nine points’polynomial transform improved FFT for high precise harmonic analysis)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2010,22(6):38-43,61.
[2]惠锦,杨洪耕(Hui Jin,Yang Honggeng).基于间谐波泄漏估算的谐波间谐波分离检测法(Harmonics and interharmonics separate-detection method based on estimation of leakage values caused by interharmonics)[J].电工技术学报(Transactions of China Electrotechnical Society),2011,26(1):183-190.
[3]牛胜锁,梁志瑞,张建华,等(Niu Shengsuo,Liang Zhirui,Zhang Jianhua,et al).基于三谱线插值FFT的电力谐波分析算法(An algorithm for electrical harmonic analysis based on triple-spectrum-line interpolation FFT)[J].中国电机工程学报(Proceedings of the CSEE),2012,32(16):130-136.
[4]刘桂英,粟时平(Liu Guiying,Li Shiping).利用小波傅里叶变换的谐波与间谐波检测(Measurement of harmonic and interharmonic using transform of wavelet and Fourier)[J].高电压技术(High Voltage Engineering),2007,33(6):184-188.
[5]程志友,梁栋,韦穗,等(Cheng Zhiyou,Liang Dong,Wei Sui,et al).基于S变换的动态间谐波检测方法研究(Dynamic detection of interharmonics based on S-transform)[J].电测与仪表(Electrical Measurement&Instrumentation),2007,44(3):5-8.
[6]李新,陈文礼,侯兴哲,等(Li Xin,ChenWenli,Hou Xingzhe,et al).支持向量机结合TLS-ESPRIT的间谐波参数估计(Interharmonics estimation using SVM and TLS-ESPRIT)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2012,24(2):67-71.
[7]张惠娟,汪友华,王艳廷,等(Zhang Huijuan,Wang Youhua,Wang Yanting,et al).基于AR模型的电力系统间谐波分析(Power system interharmonics analysis based on autoregression model)[J].电工技术学报(Transactions of China Electrotechnical Society),2010,25(7):144-149,164.
[8]李明,王晓茹(LiMing,Wang Xiaoru).基于最优窗Burg算法的电力系统间谐波谱估计(Interharmonic spectral estimation in power system based on the optimal window burg algorithm)[J].电工技术学报(Transactions of China Electrotechnical Society),2011,26(1):177-182.
[9]熊杰锋(Xiong Jiefeng).基于加窗插值和Prony的电力系统间谐波算法(Power system interharmonic analysis based on windowed interpolation and Prony algorithm)[J].电力系统保护与控制(Power System Protection and Control),2011,39(7):8-13,19.
[10]李诚诚,汪芳宗(LiChengcheng,Wang Fangzong).基于投影近似子空间跟踪算法的谐波检测方法(Projection approximation subspace tracking algorithm for harmonics detection)[J].电测与仪表(Electrical Measurement&Instrumentation),2009,46(4):21-25.
[11]沈睿佼,杨洪耕,吴昊(Shen Ruijiao,Yang Honggeng,Wu Hao).基于奇异值总体最小二乘法的间谐波估计算法(An algorithm of interharmonic estimation based on singular value decomposition total least square)[J].电网技术(Power System Technology),2006,30(23):45-49.
[12]Jain SK,Singh SN.Exact model order ESPRIT technique for harmonics and interharmonics estimation[J].IEEE Trans on Instrumentation and Measurement,2012,61(7):1915-1923.
[13]张宇辉,金国彬,李天云(Zhang Yuhui,Jin Guobin,Li Tianyun).基于自适应最优核时频分布理论的间谐波分析新方法(A novel approach to interharmonic analysis based on adaptive optimal kernel time-frequency distribution)[J].中国电机工程学报(Proceedings of the CSEE),2006,26(18):84-89.
[14]王旻鹤,刘一江,彭楚武(Wang Minhe,Liu Yijiang,Peng Chuwu).模糊神经网络优化间谐波检测方法(Optimized interharmonics estimation using Tagaki-Sugeno fuzzy model)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2011,23(3):118-122.
[15]GB/T 24337—2009电能质量公用电网间谐波[S].
[16]冯宇,唐轶,史丽萍,等(Feng Yu,Tang Yi,Shi Liping,et al).基于图形模式识别的稳态电能质量指标(The steady state power quality index based on figure pattern recognition)[J].电工技术学报(Transactions of China Electrotechnical Society),2008,23(3):108-114.
[17]冯宇,史丽萍,苗长新(Feng Yu,Shi Liping,Miao Changxin).基于图形模式识别的电能质量扰动分类(Study of power quality disturbances by figure pattern recognition)[J].高电压技术(High Voltage Engineering),2007,33(12):148-152.
