基于遗传算法的快速成形分层方法研究
2013-04-13周惠群李日华
刘 欢,周惠群,李日华
(西北工业大学现代设计与集成制造技术教育部重点实验室,陕西西安710072)
快速成形(rapid prototyping,RP)技术是20世纪80年代后期至90年代初期出现的一项新型现代制造技术,它是将计算机辅助设计(CAD)、计算机辅助制造(CAM)、计算机数字控制(CNC)、精密伺服驱动、激光技术和新材料等集于一体的新技术。自快速成形技术出现以来,CAD模型的分层技术便得到了广泛的研究。理论上,在快速成形过程中,只要切片厚度足够小,则烧结的三维实体模型与三维设计模型就应当是完全相同的。但事实上,由于受材料厚度的限制以及成形周期等因素的影响,切片的厚度不可能足够小,于是在成形零件的外形轮廓上便产生了阶梯状误差。
目前,国内外学者就如何通过改变算法来提高快速成形零件的精度做了大量研究。周满元[1]讨论了快速成形中基于STEP的直接分层算法。平雪良等[2]提出了一种提高快速成形精度的正负公差切片算法。温佩芝等[3]进行了基于有向加权图递归切片算法的研究。本文在上述研究的基础上,提出了一种新的切片算法,该方法可提高快速成形精度,且在一定程度上提高了分层的效率。
1 遗传算法
遗传算法是将问题的参数用基因表示,将问题的解用染色体表示,从而得到一个由具有不同染色体的个体所组成的群体。这个群体在问题的特定环境里生存竞争,适者有最好的机会生存和产生后代,后代随机地继承父代的最好特征,并在生存环境的控制下继续这一过程。同时,群体的染色体都将逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,便得到问题的最优解。按照以上思路,遗传算法包含选择、交叉、变异3个基本算子。
1.1 选择
适应度越大的染色体,其被复制的比例也越高。适应度最大的染色体应直接复制到下一代,以保存上一代最优的染色体,避免丢失可能的最优解;其他染色体被选择的概率为其适应度函数值占种群适应度函数值总和的百分比,被选择的染色体将进入交叉群进行交叉和变异操作。
1.2 交叉
随机地在种群中选择两条染色体 A、B,并在所选染色体中随机地选择一个交配区域进行交叉操作,其约束条件为基因值之和相等。
如:A=314 265 987,B=346 792 158;A′=314 792 265 987,B′=346 265 792 158。在 A′、B′中依次删除与交配区相同的零部件编码:A″=314 792 658,B″=342 657 918。
1.3 变异
按一定概率对进入下一代的染色体进行变异操作:100011→101001。
2 遗传算法应用于快速成形
对于分层切片而言,由于切片本身具有厚度,所以成形过程中必然产生阶梯状误差。成形时,公差在零件原始轮廓以外称为正公差,在零件原始轮廓以内称为负公差。在完成加工后,正公差将导致外型轮廓留有余料,而负公差将导致材料不足。由于受加工效率和加工工艺的影响,目前的快速成形技术多采用等厚分层切片技术(图1),其特点是不能像自适应切片技术那样根据零件结构特点的变化而变化。对于同一个零件,采用的分层算法不同,最终得到的成形精度也不同。

图1 传统分层切片
图1a和图1b是两种较传统的切片方法,分别表示对零件自上而下和自下而上进行切片。由于斜率的变化,这两种方法都将导致成形后的零件某些部位留有余料,其他一些部位则材料不足,对于精度要求较高的零件而言,均可能导致不合格产品的出现。按图1c所示的切片方法,所成形的零件整体都留有余料,这给后处理带来了较大的麻烦;图1d所示的方法则使零件整体余料不足,这有可能导致零件尺寸偏小,造成不合格现象。
本文将就以上分层方法的不足及成形零件的结构特点,提出一种新的基于遗传算法的优化分层算法。对于一个确定的零件而言,成形后的零件轮廓需留有余量的部位,可选择遗传算法中选择复制的思想,采用正公差切片,多余的阶梯状余量可通过后处理进行打磨;然而对于自由曲面的过渡部分,以往多采用随机正负公差切片算法。
针对随机算法中存在不可控性的缺点,本文提出一种新的依据遗传算法进行分层的优化分层方法。由于零件的STL模型尺寸是固定的,当给定分层厚度以后,便可求出相应的切片层数,这在计算机里很容易实现。首先对每一层切片进行编码,每一层里,如采用正公差,切片则记为1;如采用负公差,切片则记为0。这样,便得出了关于零件加工的二进制编码。在实际加工过程中,随机取出两组编码(图2)。由于零件分层后的第一层和第五层斜率较大,故以第一层和第五层作为交叉算子进行交叉,得到新的编码:0101010和1011101,对新生成的编码依次删除与交叉区域相同的编码,得到优化后的编码:01101和10110。

图2 遗传算法的二进制编码
对于本文提出的正负公差采用二进制编码的遗传算法而言,其随机编码可采用KD树的二分查找法来获得,其算法思想大致如下:
算法BUILDKDTREE(P,depth)
输入:点集P以及当前的深度depth
输出:与P对应的(k-d)树的根节点
1.if(P只包含一个点)
2.then return(存储该点的叶子)
3.else
if(depth为偶数)
4.then沿着通过P内各点x-坐标中值的垂线 l,将 P划分为左、右两个子集
(*记P1为对应于位于 l左侧或者落在l上诸点的子集,记P2为对应于位于 l右侧诸点的子集*)
5.else沿着通过P内各点y-坐标中值的水平线l,将P划分为上、下两个子集(*记P1为对应于位于l下方或者落在l上诸点的子集,记P2为对应于位于l上方诸点的子集 *)
6.vleft←BUILDKDTREE(P1,depth+1)
7.vright←BUILDKDT REE(P2,depth+1)
8.生成一个节点 v以存储直线l,并分别将vleft和vright置成 v的左、右孩子
9.return v
在开始讨论查找算法前,首先确定构造一棵二维(k-d)树所需的时间。构造过程所需时间 T(n)满足如下结论:
给定由任意n个点组成的一个集合,其对应的(k-d)树占用O(n)空间,并可在O(nlogn)时间内构造出来。
完成二维(k-d)树的构造后,在GLUT图形处理中采用拉格朗日插值查看遗传算法的效果显示,插值公式如下:
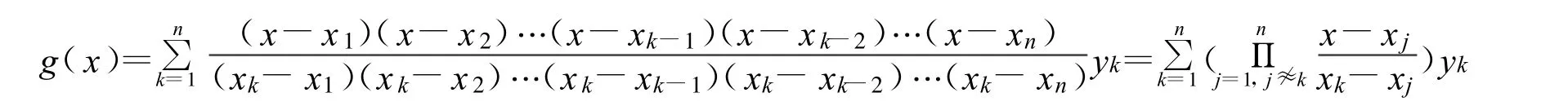
其C语言编程是很容易实现的。本文所选择的例子包含5个节点,对于更多节点的实例而言,只是N值的变化。在快速成形实际加工过程中,节点数N往往较大,如插值精度不理想,可采用分段插值的方法,即将模型的插值区间分成若干段,再对每段进行低阶插值。
在基于STL几何特征分层的模型中,对三角面片进行分类、分级快速排序后,每一面片结构都将引入两个新的数值Zmin和Zmax,分别表示在同一类面片中排列在某面片以后的面片的顶点Z坐标的最小值和最大值。
在分层过程中,对某一类面片进行交互判断时,当分层高度小于Zmin时,无须再对以后的三角形面片进行交互判断;同理,当分层高度大于Zmax时,也无须对以后的三角形面片进行交互判断。这样,在分层过程中,随着分层高度的变化,减少了与其他面片不必要的相交关系的判断,从而提高了分层处理的速度。
3 运算实例结果
图3是采用传统算法和遗传算法对模型进行分层切片的示意图。基于遗传算法的STL切片模型采用了优化的三角面片分隔,相比于传统的STL三角面片分隔,能有效避免误差的累积。对于面片较少的零件而言,采用遗传算法进行分层切片,与文献[3]中的方法相比,在效率方面无明显优势;对于面片较多的零件而言,采用遗传算法进行分层切片,与文献[3]中的方法相比,其效率有了较明显的提升。详细参数及效率对比见表1。
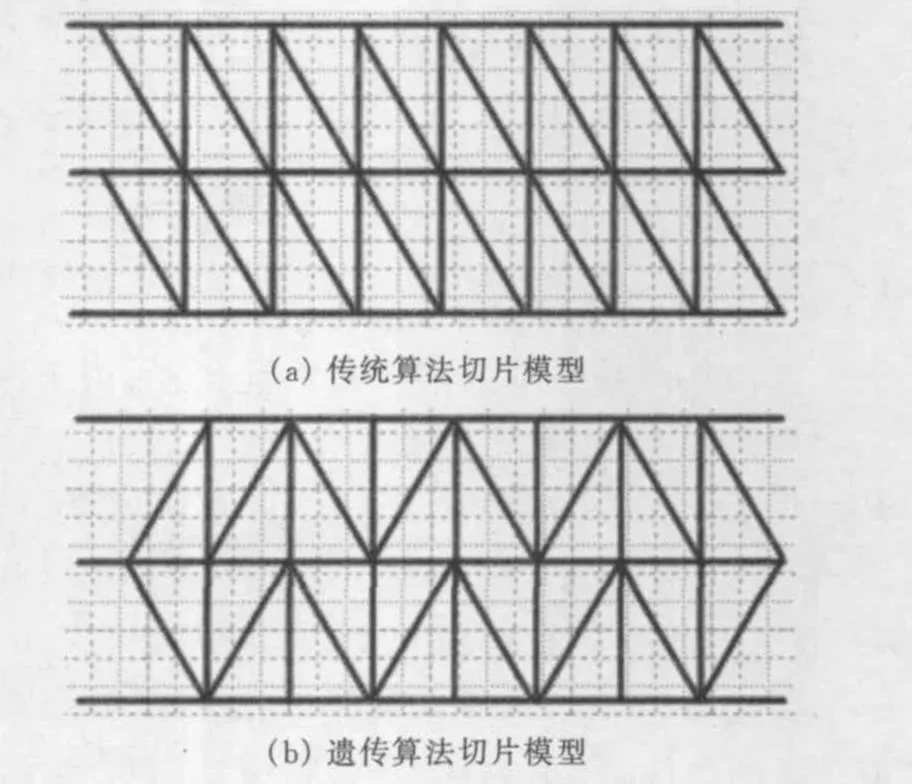
图3 两种算法实例比较

表1 STL模型切片算法的模型参数及切片耗时对比
4 结语
本文在文献[2]和文献[3]的基础上,提出了一种新的算法,该算法能有效解决对精度要求较高的零件的分层切片问题,并在一定程度上提高了分层切片的效率。
[1] 周满元.一种非均匀自适应分层方法[J].计算机工程与应用,2005(3):72-75.
[2] 平雪良,高同军,孟凡虹.一种提高快速成形系统精度的新切片算法[J].机械科学与技术,2008,27(9):1121-1124.
[3] 温佩芝,黄文明,吴成柯.一种改进的ST L文件快速分层算法[J].计算机应用,2008,28(7):1766-1768.
[4] 李广慧,王丽萍,于平,等.SLS激光快速成形烧结层厚的选取[J].煤矿机械,2003(3):27-29.
