多功能角度规的测量新方法

扬州冶金机械有限公司 （江苏 225009） 茅保富

多功能角度规的测量新方法

扬州冶金机械有限公司 （江苏 225009） 茅保富

在车床和磨床上经常会加工高精度外锥体的工件，锥度和大、小端直径测量困难。通常的测量方法是采用锥度环规与外锥体互研的办法，该方法笨重且测量精度不高，一种锥度规只能测量一种锥体，既不经济效率又低。用正弦规测量锥度精度很高，但它必须在精密平台上进行测量，且不能测量大、小端直径，更不能在机床上使用，局限性较大。现将正弦规稍加变形和改进，即可在机床上测量外锥体锥度、各种工件角度和与之相关的大小端直径和长度尺寸，并可测量多种形位误差和缺圆、超大尺寸内外圆直径。该量规可称之为多功能角度规。

1.多功能角度规检测

图1为多功能角度规结构示意图，角度规由两根圆柱、两根圆柱之间垂直固定的固定座和固定座一侧经螺钉联接的两块定位板构成。固定座呈槽钢形状，其两端下部加工成V形直角状，用螺钉将圆柱拧紧在固定座上，固定座侧面与V形直角面垂直。圆柱两端分别突出固定座20～30mm , 两圆柱之间的距离为整数值。固定座两端间的长度小于两圆柱外侧母线间距离2mm以上。固定座上平面两端开有矩形缺口。

图1 多功能角度规

2.外锥体锥度和大端直径测量

图2所示为外锥体锥度和大端直径测量方法示意图，将拆去定位板的两个角度规放在锥体上下母线处，用两组等长小弹簧连接在测量圆柱端面固定螺钉上，拉紧下面角度规贴紧锥体下母线，左端测量圆柱利用锥体小端面吸住磁块并同时吸住弹簧片顶住角度规与锥体大端面相切，力度以能让角度规自由摆动即可（亦可在固定座上加上磁块，将测量圆柱吸在锥体上，左侧圆柱与锥体大端面相切。下面角度规可与锥体吸牢，上面角度规吸力调节到能吸住锥体大端面但能自由摆动为宜）。用千分尺量得M1、M2尺寸， 代入公式

即可求得锥度和锥体大端直径。

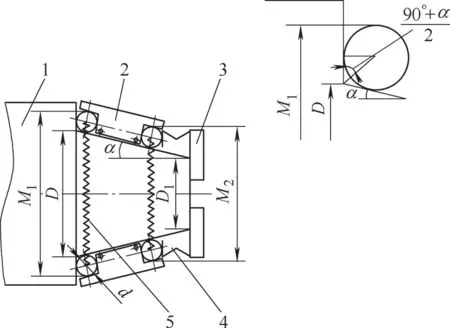
图2

例：一外锥体锥度，图样要求为1∶10（锥角为5°43′29.3″），大端直径φ（100±0.02）mm。测得外锥体M1为139.04 mm，M2为129.05mm。多功能角度规测量圆柱直径为20mm，测量圆柱间距离为100 mm。

解：将M1、M2代入公式，得

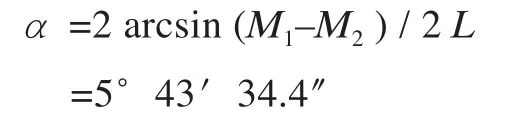
计算结果比图样要求5°43′29.3″（1∶10）大5.1″，将M1和α代入公式，得

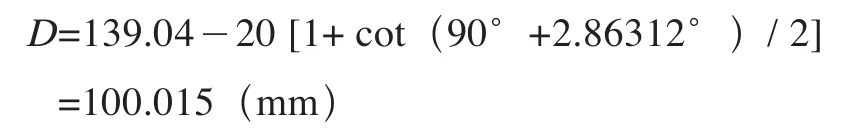
该工件符合图样要求。

工件完工后从机床上卸下，可将锥体小端向上垂直插入方箱孔内测量，只需一组小弹簧拉住上方测量圆柱贴住锥体即可测量，测量将更加方便。

测量小端直径时，将两组角度规右移，用磁块吸住外锥体小端端面和测量圆柱，用外径千分尺量得M1、M2尺寸后, 代入公式

2α= 2 arcsin (M1-M2) / 2L(L为两圆柱间距离)

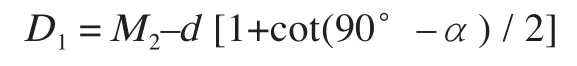
则可得到锥度和小端直径尺寸（方法同角度小端尺寸测量，见图3）。

3.角度及相关长度尺寸测量

图3所示为角度及相关长度尺寸测量方法示意图，用磁块吸住工件右侧面和多功能角度规测量圆柱，保证测量圆柱母线与右侧面在同一平面上，直接用外径千分尺测得M1和M2，代入公式

α= arcsin (M2-M1) /L(L为两圆柱间距离 )

L1=M1-r[1+cot ( 90°-α ) / 2] (r为测量圆柱半径 )

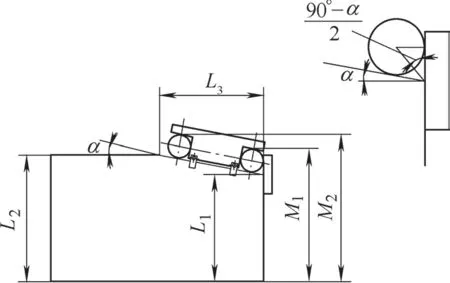
图3

即可求得角度和相关长度尺寸。

例：一工件斜角，图样要求为15°±30″，L3长度为（200±0.03）mm。量得M1为189.49 mm，M2为215.36 mm，L2高度为200.02 mm。多功能角度规测量圆柱直径为20mm，测量圆柱间距离为100 mm。

解：将M1、M2代入公式，得

比图样要求15°±30″ 下差小5.4″。将M1和α代入公式，得

将L1、L2和α代入公式，得

结论：该工件符合图样要求。

4.轧机牌坊垂直度、对称度、位置度的测量

图4为轧机牌坊垂直度、对称度、位置度的测量示意图，测量时，把两个（测量面长度较大时用四个）角度规分别靠在牌坊互为垂直的M、N面上，将圆柱面贴紧测量面，Ν面D圆柱同时与X面贴紧，两定位块靠在上平面上，保证两圆柱中心线与上平面垂直， 将其固定。 用内径千分尺分别测量AC、AD、CD尺寸（内径千分尺下端可套上定心卡套与测量圆柱自动定心，定心卡套见图6），然后将AC、AD、CD尺寸代入余弦定理公式，求得∠D。以C、D为横坐标，D点为原点，再根据正弦和余弦函数即可求得A点横向和纵向坐标。同理，可求得B点坐标，然后根据A、B两点横坐标距离之差以及A、B两点纵向距离与总高度之比即可求得垂直度误差。

将C、D处角度规移至E、F处，E圆柱与O、Y面相切，将其固定。根据XY、XM、BE尺寸求得B点横向和纵向坐标。把B点与E点横向距离减去牌坊内档一半所得之尺寸和X点与M点横向距离加上牌坊内档一半所得之尺寸相比，所得之差即为对称度误差；同理，B点与D、E点纵向距离之差即为Ν面和O面位置度之差。

图4

例： 测得A、C圆柱间距离为1996.90mm，A、D圆柱间距离为1932.41mm，C、D圆柱间距离为380mm，B、C圆柱间距离为1332.41mm，B、D圆柱间距离为1234.21mm。测量圆柱直径为20mm。

求垂直度误差：将AC、AD、CD代入余弦定理公式，得

作A点垂直于C、D延长线的垂点A′，则

Rt△AA′D直角边DA′= 119.98mm。

将BC、BD、CD代入余弦定理公式a²=b²+c²-2abcosA，得

cos∠BDC= = -0.095647941

∠BDC= 95.48861397°

作B点垂直于C、D延长线的垂点为B′，则

Rt△BB′D直角边DB′ = 119.96mm。

AB与CD垂直度误差A′B′为

DA′B′-DA′B′= 119.98-119.96=0.02（mm）

因为M面长度约为AB长的2倍，所以M面与N面的垂直度误差为

2A′B′ = 2×0.02 = 0.04（mm）

求对称度误差：测得X、Y外开挡尺寸为1199.95 mm，M、P内开挡尺寸为1000.06 mm。

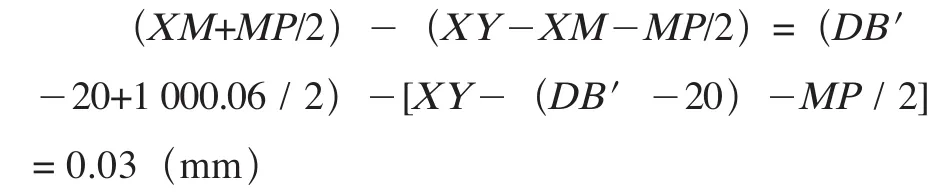
即X、Y中心与M、P中心的对称度误差为0.03mm。

求位置度误差： 测得B、E圆柱间距离为1643.91 mm。

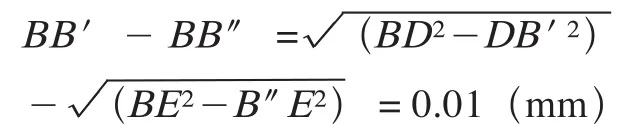
通过以上计算得到N面与O面的位置度误差为0.01 mm。

5.缺圆和超大直径内外圆直径测量

图5所示为缺圆和超大直径内外圆直径测量方法示意图，将三组角度规靠在内外圆柱面任意三点处，并将其固定。用内径千分尺测量三组角度规三点间距离，将其数值代入余弦定理公式，求得任意一角度，再代入正弦定理公式计算，所得之尺寸加上或减去一个测量圆柱直径即为所求内外圆之直径。

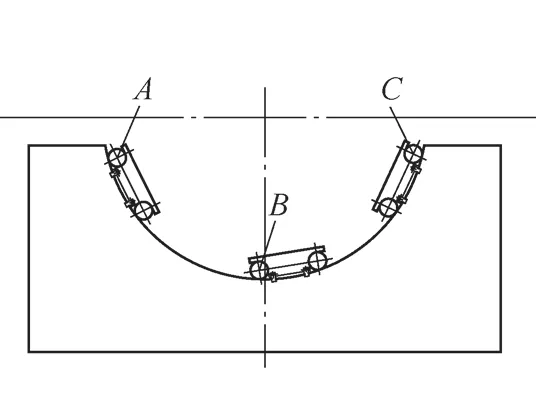
图5

例：量得A、B圆柱间距离为1216.68 mm，A、C圆柱间距离为1976.09 mm，B、C圆柱间距离为1324.44 mm。

（1）将AB、AC、BC代入余弦定理公式，得：

（2）将∠ACB代入正弦定理公式，得：

2R=2035.04（mm）

该尺寸为测量圆柱圆心之直径，加上测量圆柱的直径即为缺圆直径

2035.04+20 = 2055.04（mm）

计算结果：该缺圆直径为2055.04mm。

温馨提示：用内径千分尺测量时，要考虑到温度对测量尺寸的影响。当气温较低时，要将内径千分尺用隔热材料包裹好，否则测量误差较大，影响测量精度。

20121204）