基于混联机构的多自由度风洞动态试验平台运动学研究

李士佩，李鹭扬，牛瑞霞，蒋波

(扬州大学 机械工程学院，江苏 扬州 225127)

0 引言

在风洞［1］试验中，被测量的飞行器动态地任意改变其飞行姿态，这是飞行器风洞试验的一个非常重要的试验项目。混联机构可以满足多自由度风洞动态实验的要求，其中混联机构的机构学与运动学主要集中在机构的运动正反解问题［2-5］、工作空间、奇异位行和灵巧度分析等方面［6-7］。风洞试验运动平台是风洞试验时重要的运动装置，该平台提供实验模型所需的位置和姿态。该平台性能的优劣对风洞试验数据的获得有着重要影响，因为不仅要求风洞流场干扰小，不影响模型气动外形模拟，还要求结构简单、动态性能好、体积小、成本低和应用范围广等［8］。本文描述了五自由度混联机构的工作原理，并运用数值分析法［9-12］对模拟实验平台并联部分位置正反解进行了分析。因为该机构的并联部分与串联部分相互影响，因此在得到位置正反解的基础上求得并联部分与串联部分相互关系非常关键，从而推出模拟平台的末端在风洞试验中的位姿。

1 风洞实验运动平台工作原理及坐标系的建立

1.1 运动原理

风洞实验运动平台采用串并联混合的方式，实现实验模型质心在风洞固定点的五自由度的运动，其原理如图1 所示。

图1 风洞实验运动平台

图1 为运动平台的实物图，上平台和下平台之间为三条支链，每条支链由一个电动缸和两个回转关节组成，三条支链布置在平行于xoy 平面的三个平面内，形成一个三自由度的平面并联机构，该机构可以沿x 和y 方向移动和绕垂直于平面z 轴的转动，下平台可以沿着x 轴移动。通过该并联机构，可以改变飞行器模型在风洞中的角度变化，同时，补偿由于采用尾支杆而引起的运动平台的位移变化。在运动平台上有一个回转关节，其回转轴线MN 在平面xoy 内。弯刀装置绕该轴线做回转运动，控制飞行器模型的偏航角。弯刀装置的另一端通过一个回转关节连接尾支杆，尾支杆通过做绕体轴的滚转运动控制飞行器模型的滚转角。而该平台的模型体轴上的点M 是不变的，做偏航运动的时候沿着轴ML 转动。

1.2 坐标系的建立

建立基础坐标系{B}:坐标原点与模型质心重合，z 轴方向垂直于3-RPP 机构所在平面，x 轴方向与下平台导轨方向一致;3-RPP 机构下平台连体坐标系{F}:方向与{B}一致，初始位置为下平台大致处于轨道中点处，坐标原点在最左侧铰链F0 处，与模型后端对应，即BPFROG=BPF0;3-RPP 机构动平台连体坐标系{M}:初始方向与与{B}一致，原点与模型质心重合;试验连体坐标系{T}:原点位于模型质心处，x 轴与模型体轴一致，初始方向为将{B}绕其z 轴旋转至x 轴与模型体轴一致;弯刀连体坐标系{W}:原点与模型质心重合，初始方向与模型连体坐标初始方向一致。

2 运动平台混联机构闭环反馈的正解

2.1 运动学关系

串－并混联机构如图1 所示，并联部分的上平台通过三个驱动电动机分别连接动平台顶点Ai和底座的顶点Bi，P 和R 分别表示动平台原点在参考坐标系中的位置矢量和姿态的变换矩阵。根据动平台的姿态角和移动位移就可解出电动缸的矢量，即:

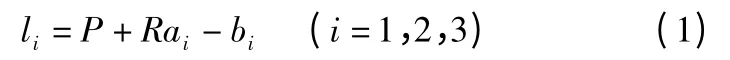
式中:ai，bi分别是两平台顶点在各自坐标系中的位置矢量。Lis是并联机构电动缸支撑杆的矢量，(i=1，2，3)。

根据式(1)，各动平台顶点的速度可写成如下形式:

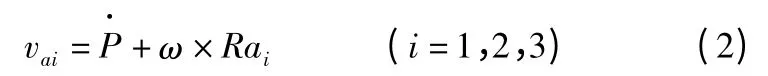
式中:ω——在参考坐标系中动平台的角速度;

式(2)写成矩阵型式为:

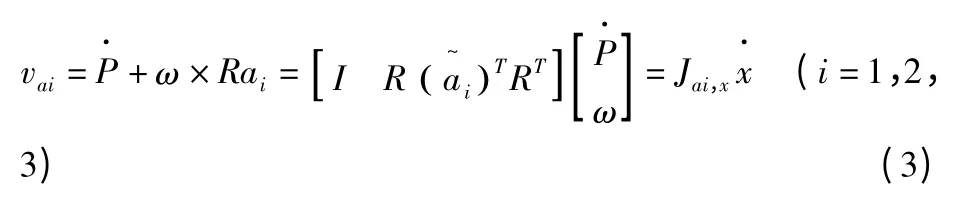
Jai，x——是动平台广义速度到动平台上顶点速度的雅克比矩阵。

将动平台上顶点速度向电动缸伸缩杆矢量方向投影，可得它们的伸缩速度:

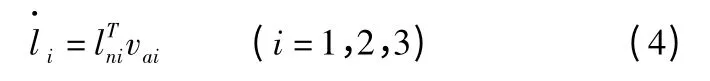
lni——电动缸伸缩杆的单位矢量，lni=。

将式(2)代入式(4)有:

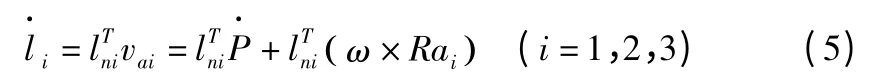
由于并联机构有三个电动缸伸缩杆，可以将式(5)写成矩阵形式:

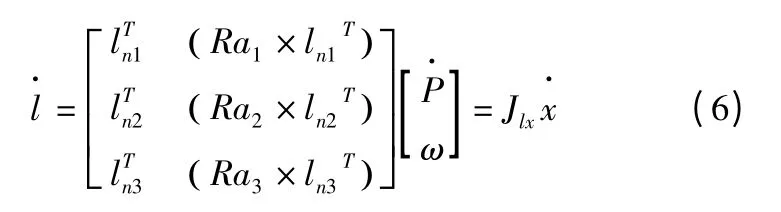
Jlx——并联机构广义速度到电动缸伸缩杆伸缩速度的雅克比矩阵。

a)运动学正解

运动学正解的问题是分析和设计并联机构的关键，本节对试验平台的并联部分的运动学正解算法进行研究。并联机构的运动学正解就是在已知电动缸伸缩杆长度的情况下求解动平台的姿态，通常并联机构的运动学正解比运动反解复杂。这里主要借鉴Stewart 机构的运动学正解算法，求解非线性方程组:

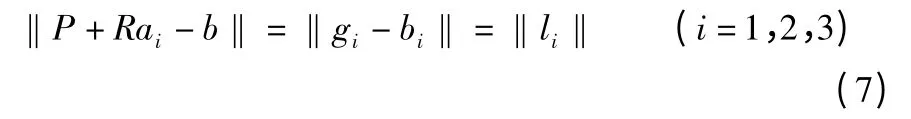
用牛顿-泰勒展开法求解上述非线性方程组(7)，此方程组也可表达如下:

式中:li0——电动缸伸缩杆的初始长度(mm);

Δli——电动缸伸缩杆的变化量(mm);

gki——电动缸伸缩杆在动平台上的接触点在参考坐标系中的坐标，k=1，2，3;

bki——底座在参考坐标系中的坐标，k=1，2，3。

令:

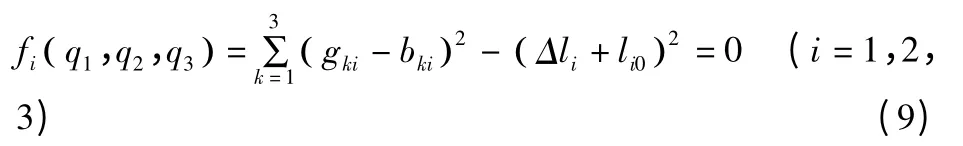
解如式(9)所示的非线性方程组，其中q1，q2，q3分别为上平台的绕z 轴的转角，沿x 和y 轴的位移，即可求出动平台的当前姿态q。将fi(q) 在初始位置q0附近进行泰勒级数展开，并取其线性部分得:

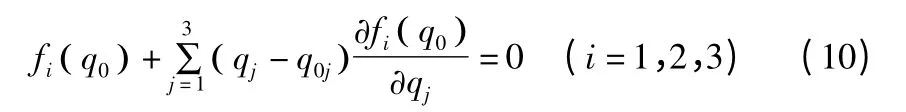
进一步令:Δq=q－q0和Δqj=qj－q0j(j=1，2，3)，则式(10)可写为:

式(11)可以看成是Δqi(i=1，2，3)为未知数的方程组，其系数矩阵用J1表示为:

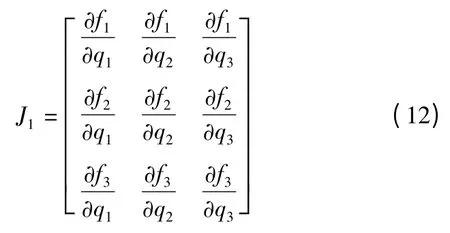
如果J1是非奇异矩阵，则方程组(3－ 12)有唯一解Δq。

若Δq 可以满足精度的要求，即Δq≤ε(ε 为要求精度)，则q=q0+Δq 是所要求的正解;否则令q0=q，根据新的赋值重复计算电动缸伸缩杆的长度li0(1，2，3)和系数矩阵J1，然后根据式(11)再次求解Δq，直到Δq 在要求的精度范围内为止。以上是用牛顿—泰勒展开法求解非线性方程组(7)的数值方法，即牛顿迭代法。求系数矩阵J1是这种解法的关键。

对式(9)求qj(j=1，2，3)的偏导数可得:

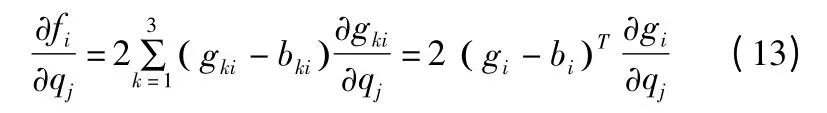
由以上的条件可知:

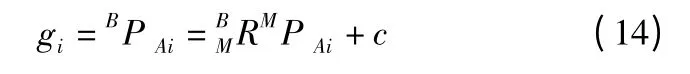
其中:

为方便以下的计算令cα=cosα，sα=sinα。根据式8与式15 可得到

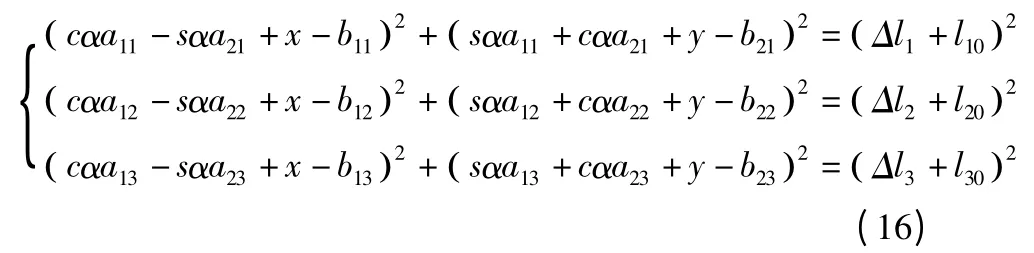
b)运动平台混联机构与串联的关系

这里主要研究的是模型的俯仰角θ，偏航电动机转角β和滚转电动机转角为γ 之间的关系，由上述的公式(16)可以求出动平台的俯仰角α。根据时间轴上每一节点对应模拟平台的俯仰角θ(常量)及偏航电动机角度φ，滚转电动机转角为γ，求得模型连体坐标系{T}在基础坐标系{B}中的姿态表示，其转动为先绕z 轴转α，后绕y 轴转φ，所以:

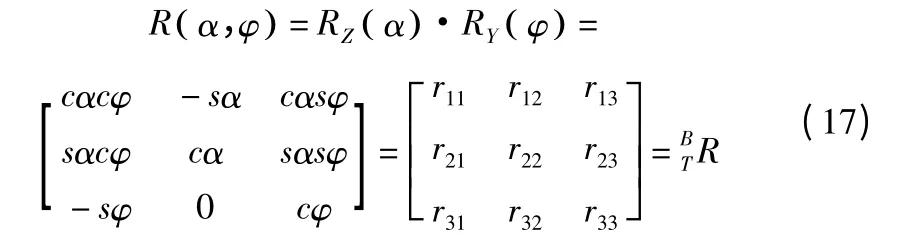
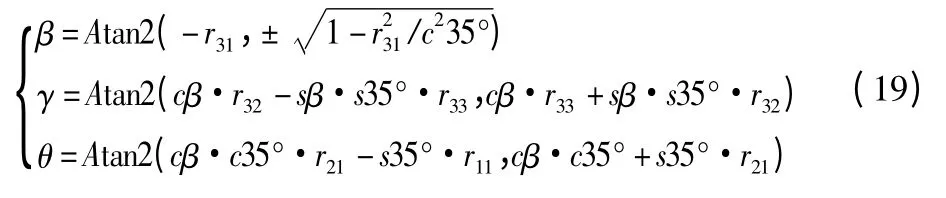
3 机构动平台混联机构闭环反馈的反解

设动平台上的3 个关节点分别表示为M1，M2，M3，下平台上3 个关节点分别表示为F1，F2，F3，动平台俯仰角α，3 个电动缸的长度分别为l1，l2，l3。

单独的俯仰运动可以通过三个电动缸的伸缩和下平台的移动来完成，时间轴上每一节点对应的动平台俯仰角α(动平台的俯仰角与模型的俯仰角相差35°)及下平台连体坐标系坐标原点在{B}中的坐标值BPFROG，x 为坐标值的初始值即F0 点至模型质心的x 方向的初始距离;y 方向坐标值y 为F0 点至模型质心的y 方向距离;z 坐标值为零。

根据坐标系的设定有:

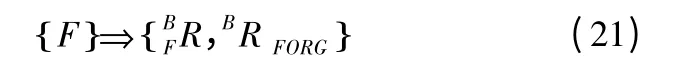
式中:

因此有:

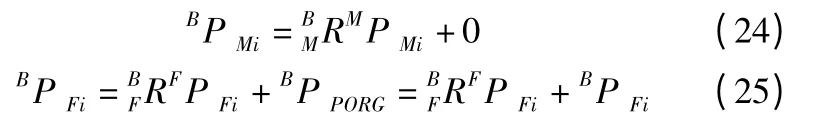
以得到:

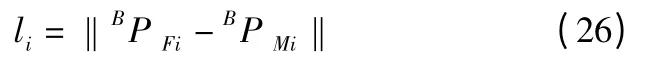
具体表达式如下:

因此，若已知α，下平台连体坐标系坐标原点在{B}中的坐标值BPFRoG和动平台Mi 各点在{B}中的坐标值可求出各个电动缸的长度，反解得以求出。

4 运动平台正反解分析

4.1 正反解问题的解法选择

由于本文讨论的五自由度混联机构的复杂性，从而该机构位置正反解的数学模型是比一般线性方程组复杂的非线性方程组。因此，对这种机构位置正反解的数学模型进行解法分析［5］是有必要的，通过以往对位姿正反解的研究成果的了解，这种复杂数学模型的解法主要有两种:

1)解析法:解析法从一组约束方程中通过消元除去未知变量，可以得到单变量的多项式方程。末端执行器的所有位姿的可能包含了该一元多项式方程的实根。但是解析法不能明确地看出变量的数量关系、不够直观。

2)数值法:数值法的数学模型比较简单，如果要求有一个实解，有好的初值的多数情况下，直接用非线性方程的求解算法，避免了繁琐的数学推导，计算速度比较快。

对于复杂的非线性方程组的求解［6-7］，大多数采用数值的方法，即通过特定的算法，利用计算机对方程组求解，求得方程组的数值解。如果采用直接消元法，即使可以得到一个变量的单个方程，但是会出现大量增根和数值不稳定的情况，因此一般不采用直接法求解。本文用数值解法的基本过程是根据混联机构先建立数学模型、讨论数值计算方法、程序设计、上机计算出结果。

本文采用修正牛顿迭代法对五自由度混联机构的并联部分正反解方程组的求解实现以上的算法，并求得并联与串联部分的关系。应用Matlab［8］软件编制程序来求解本文所分析的五自由度混联机构的位置正反解方程组［9］。通过定义机构初始参数，确定计算机位置正反解函数，进入修正牛顿迭代计算，确定正反解函数的Jacobi矩阵［10-11］等过程对计算进行了功能模块化。计算机就可以进行规定次数的迭代，并输出每一次迭代后的数值，最终得到理想的数值。

4.2 机构数值解法实例

为了验证以上程序，本节给出了对五自由度混联机构在风洞试验中末端模型位姿的实例，当风洞模拟实验平台做振幅是30°，支撑角是35°时的俯仰运动及振幅为20°，俯仰角度是10°的偏航运动时候各个电动缸的长度值如表1 所示。

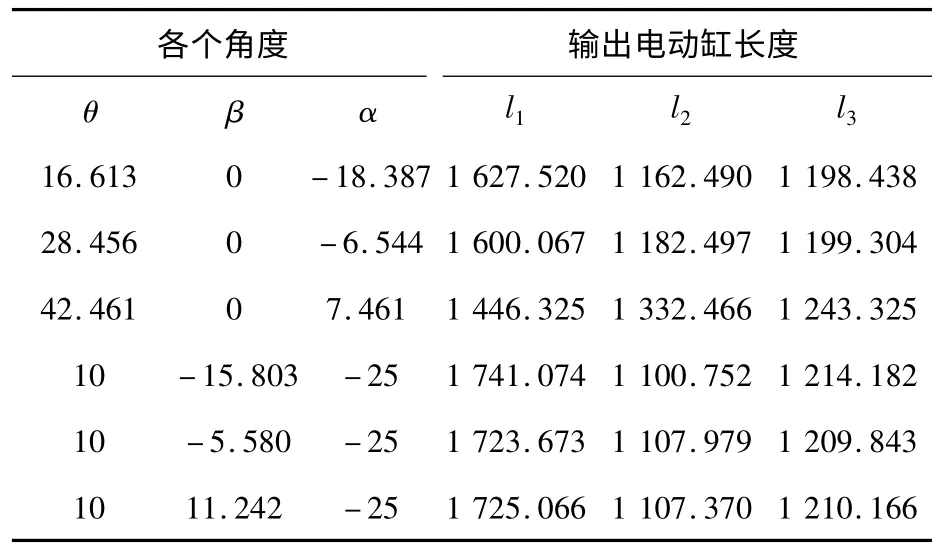
表1 五自由度机构位置反解数字迭代实例

5 结语

本文介绍了风洞试验虚拟样机的运动原理，并将混联机构用于风洞试验，实现了飞行器在风洞中多自由度的运动，突破了以往运动试验装置只能实现一个或两个自由度的限制。这里分析的五自由度混联机构是根据得到的混联机构的位置正反解的方程组，将并联和串联的运动分析巧妙的结合起来以求得末端执行器的位姿与电动缸各支链长度的变化关系。在修正牛顿迭代法的基础上利用了Matlab 数学工具对其运算的过程进行编程，最后得到需要的数据。这种方法简化了试验模型的运动分析，是机构运动学分析的一个突破。

［1］贺德馨.风洞天平［M］.北京:国防工业出版社，2001.

［2］代小林.三自由度并联机构分析与控制策略研究［D］.哈尔滨:哈尔滨工业大学，2009:38-42.

［3］韩书葵，方跃法，任红亚.一种五自由度并联机器人奇异位形［J］.中国安全科学学报，2005，15(11):28-29.

［4］John J.Craig.Introduction to robotics:Mechanics and Control，Third Edition.［M］.北京:机械工业出版社，2006.19-70.

［5］袁东锦.计算方法—数值分析［M］.南京:南京师范大学出版社，2007.149-162.

［6］陈文家，赵明扬，房立金.基于四自由度并联机构的数控机床研究［J］.扬州大学学报，2001，4(2):50-54.

［7］Dai Xiaolin，Huang Qitao etal.Accuracy synthesis of Stewart platform used in testing system for spacecraft docking mechanism.International Conference on Measuring Technology and Mechatronics Automation，2009，vol3:7-10.

［8］张志涌，杨祖樱.MATLAB 教程R2010a［M］.北京:北京航空航天大学出版社，2010.71-111.

［9］王军.并联机器人机构运动学分析及控制系统的研究［D］.南京:南京农业大学，2007.5-16.

［10］G.P.He，X.L.Tan，X.H.Zhang et al.Modeling，motion planning，and control of one-legged hopping robot actuated by two.arms.Mechanism and Machine Theory，2008，43(1):33-49.

［11］D.Stewart.A platform with Six degrees of Freedom［J］.Proceedings of the IMechE，1965，66(15):371-385.

［12］Liu H T，Huang T，Mei J P，et al，Kinematic design of a 5-DOF hybrid robot with large workspace/limb-stroke ratio，ASME Journal of Mechanical Design，2007，129:530-537.