大型回转窑筒体的力学分析与计算
2013-04-09张波景作军
张波,景作军
(北方工业大学 机电工程学院,北京 100144)
回转窑是对散状或浆状物料进行加热处理的热工设备,问世已经逾百年。回转窑广泛用在建材、冶金、化工、环保等许多生产行业中,广泛地使用回转窑对固体物料进行机械、物理或化学处理。回转窑的外形与结构组成见图1。

图1 回转窑结构图
回转窑筒体长,跨距大,为保证回转窑长期安全运转,要求筒体在横断面上具有较大的刚度,在纵向则要具有较好的柔性,直而圆直接关系到回转窑内衬砖的寿命和窑的运转率。然而在实际运转中,由于窑体变形,窑体和支承装置安装误差,基础下沉等客观原因,使得窑筒体既不直也不圆,造成薄壁筒体不仅具有轴向应力和变形,还有不可忽视的环向应力和变形[1]。
近20 年来,许多学者在这方面做了努力,但是筒体的内力和变形比较复杂,而且各家的观点也不一致,所以,至今也未得到理论上成熟,使用方便的计算公式。目前,国内外仍引用一些假设条件,一般将筒体简化为连续梁,用材料力学的方法计算,然而将复杂三维问题简化为一维杆件问题时,只能计算筒体的轴向应力和应变,而不能得到筒体的环向应力和环向变形[2]。
严格意义上来讲,大型回转窑筒体的力学分析与计算是一个三维板壳问题。为了更全面的探求回转窑筒体的应力应变分布状况,本文深入推导了回转窑筒体在非简支边时法向载荷作用下的位移函数,并在求解位移函数的16 个未知数时给出了合理的边界条件,最后导出了回转窑筒体在法向均布载荷作用下各向应变应力的解析解,这些解为优化筒体设计时提供理论依据。
1 大型回转窑筒体力学模型的建立
本文研究对象为d4.8X 74 的回转窑,该窑共有4 档支承,结构如图2 所示。

图2 回转窑4 档支承
截取3-4 档进行分析,筒体断面如图3 所示,筒体长度l=22 m,筒体厚度t=0.032 m,E=2.1×10^11 Pa,v=0.3,均布载荷q 作用在下半圈内。将回转窑3-4 档的筒体简化为连续梁,如图4 所示,根据三弯矩方程[3]求得3~4 档左端面弯矩为-531.35 t·m,右端面弯矩为-679 t·m,进而求得左端面最低点处轴向应力为-9.361 7e +006 Pa,右端面最低点处轴向应力为-1.196 3e+007 Pa。
法向载荷作用下,回转窑筒体的基本微分方程为[4]:



若引用位移函数F=F(α,β),把中面位移表示成:
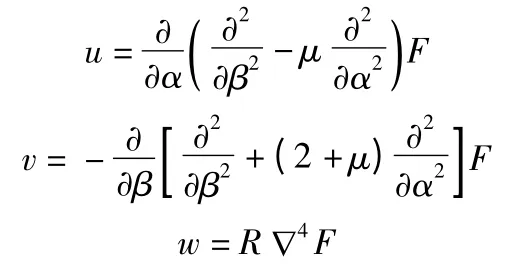
则式(1)中的前两个方程总能满足,而第三个方程则要求:

回转窑筒体的两端为非简支边,可以用β 的三角级数求解。取位移函数为[4]:

将式(3)代入式(2)有:

将q3(α,β)展成周期为2πR 的傅里叶级数[5]:

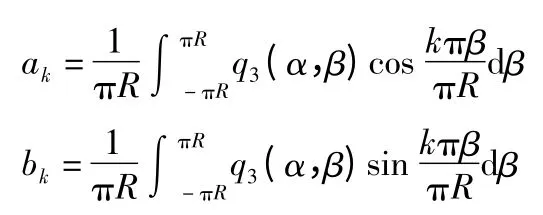
将式(5)代入式(4),比较式(4)左右两边系数,有:
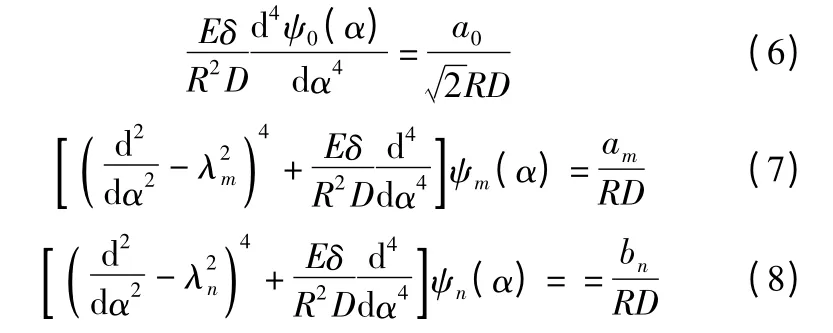
由微分方程式(6)可知:

由微分方程式(7)可知其特征方程为:
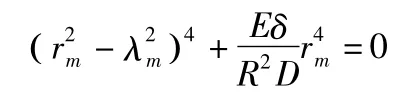

其中am,bm,cm,dm均为实数,m 取1,2,3,4。
那么:

同理:
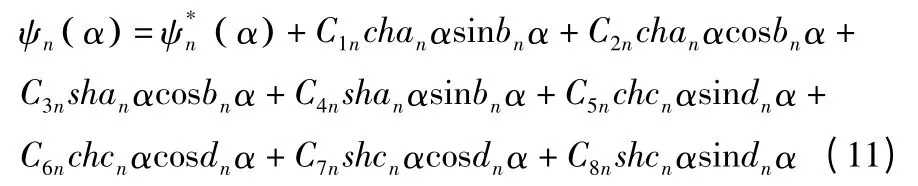
取法向载荷q3(α,β)=q,且

2 理论计算
非简支边条件下,回转窑筒体两端的边界条件为:
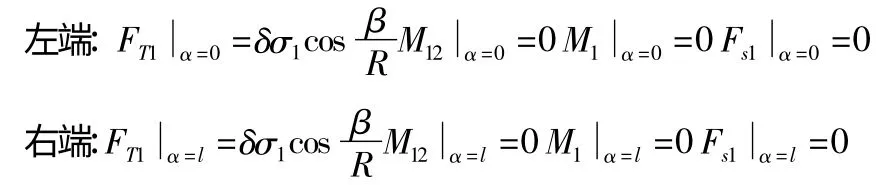
FT1为回转窑壳面纵向拉应力;M12为回转窑壳面扭矩;M1回转窑壳面弯矩;Fs1为回转窑壳面剪力;σ1为筒体左右两端的横向拉应力。

其中:fmi=
边界条件:

比较式(12)和式(13)得到:
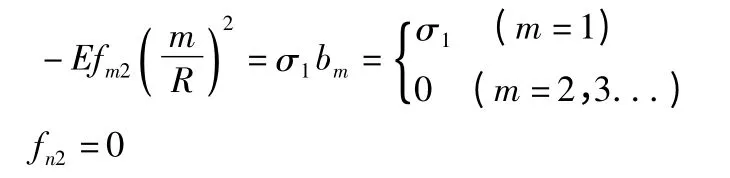
将α=0,α=l 两端的边界条件代入可得四个方程。
同理,可将M12,M1,Fs1展开,并将两端的边界条件代入,一共可得到16 个方程,这16 个方程可将F(α,β)中的16 个未知数C1m-C8m,C1n-C8n求出。
通过MATLAB 辅助计算[6],当m=1 时,

当m=2 时,c1m,c2m,…,c8m=0;c1n,c2n,…,c8n=0
2.1 回转窑位移解析解

Hu随α 变化的曲线如图5 所示。

图5 Hu随x 变化曲线

Hv随α 变化的曲线如图6 所示。

图6 Hv随x 变化曲线
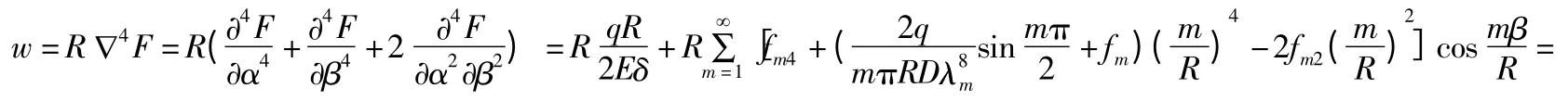

Hw随α 变化的曲线如图7 所示。

图7 Hw 随x 变化曲线
2.2 回转窑应力解析解
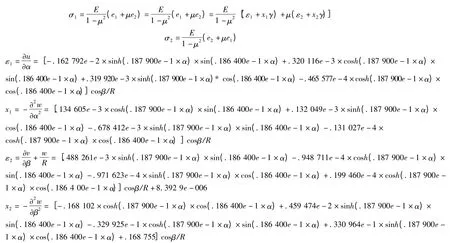
3 结论
根据梁理论和壳体理论,并对回转窑筒体在非简支边时法向载荷作用下的位移函数进行深入推导,结合合理的边界条件,求出了位移函数中的16 个未知数,最后导出了回转窑各向应变应力的解析解。根据这些解析解,可以求出回转窑在任意点处的应力和变形,找出筒体的危险薄弱点和面,从而为回转窑筒体的设计及调整提供理论指导。
[1]江旭昌.回转窑托轮的调整(一)[J].新世纪水泥导报,2000,5(2):36-40.
[2]肖友刚.多支承回转窑接触体系的力学特征研究及参数优化[D].长沙:中南大学,2004.
[3]刘鸿文.材料力学[M].下册.北京:高等出版社,2004.89-92.
[4]徐芝伦.弹性力学[M].下册.北京:高等教育出版社,2006.197-200.
[5]同济大学数学系.高等数学[M].6 版,下册.北京:高等教育出版社,2007.4.
[6]陈怀琛,龚杰民.线形代数实践及MATLAB 入门[M].2 版.北京:电子工业大学出版社,2009.
