基于模糊自适应PID 技术的励磁控制器研究

楚清河，李卫华

(华北水利水电学院 电力学院，河南 郑州 450011)

0 引言

同步发电机的励磁控制系统对提高整个电力系统的稳定性起着至关重要的作用，良好的励磁控制可以保证发电机的可靠运行，提供合格的电能，而且可以提高电力系统的静态和暂态稳定极限。常规的PID 励磁控制器以发电机的机端电压的偏差量为输入，通过比例、积分和微分环节作用于控制对象，达到自动调节机端电压的目的。其结构简单，容易实现，具有一定的鲁棒性，稳态无静态误差，控制精度高，能够满足大部分工业系统对自动控制的要求，广泛应用于工业过程控制。由于电力系统是一个复杂的巨大的非线性系统，具有时变性和参数不确定性，想要精确地描述电力系统的数学模型是相当复杂难以实现的，因而使得常规PID 控制难以达到满意的控制效果。

而模糊控制可以不依赖与系统的精确数学模型，逐渐成为研究改善控制系统性能的热门方向。为了克服常规PID 励磁控制器的缺点，人们把模糊控制原理和PID 控制相结合，通过人们在学习和实验过程中长期积累而逐渐形成的模糊控制规则，在线实时控制PID 控制器的比例、微分和积分环节参数，使得三个参数向人们预期的方向发展，从而获得良好的控制效果。利用MATLAB 中的模糊逻辑工具箱可以很方便的对设计的模糊PID 励磁控制系统进行仿真研究，通过与常规PID 控制对比可以看出模糊PID 控制的优越性。

1 同步发电机励磁控制系统的数学模型［1］

模糊控制可以不依赖精确的被控对象数学模型，所以本文采用简化的励磁系统数学模型进行仿真研究。简化的励磁系统模型由励磁调节器、同步发电机、移相触发和功率放大单元、电压测量比较单元组成。要精确描述发电机的数学模型是相当复杂的，在研究励磁控制时只研究发电机空载时励磁控制系统的有关性能，可以把同步发电机用一阶滞后环节来近似描述，传递函数为，KG表示发电机的放大系数，Td表示其时间常数;移相触发和功率放大单元:电子型励磁调节器的功率放大单元是晶闸管整流器，由于晶闸管整流元件的工作是断续的，其输出平均电压与触发器控制电压信号存在着时滞，最大可能滞后时间为1/mf，m 为整流电路控制相数，f 为电源频率，因此，包括触发器在内的晶闸管整流器的传递函数为G(s)=，对其进行泰勒级数展开并略去高次项可得简化后的传递函数为，KZ为电压放大系数，TZ为放大单元的时间常数;电压测量比较单元由测量变压器、整流滤波电路及测量比较电路组成，由于整流滤波电路有延时，用一阶惯性环节来近似描述，传递函数为，KR为电压输入输出比例系数，TR为电压测量回路的时间常数，数值通常在0.02～0.06 s 之间。

2 模糊自适应PID 励磁控制器的设计［2-3］

2.1 模糊自适应PID 励磁控制器的结构设计

本文设计的是一个二维模糊控制器，以系统误差e 和系统误差变化率ec 为输入变量，令EC=de(t)/ dt，通过专家经验形成模糊控制规则推理出PID 参数Kp，Ki，Kd的变化量ΔKp，ΔKi 和ΔKd 作为输出量，对PID 的原有参数进行在线整定，以满足不同误差和误差变化率对控制器参数的不同要求，从而达到良好的控制效果。模糊PID 励磁控制器的结构如图1 所示。

图1 模糊PID 控制结构图

2.2 确定输入和输出的隶属度函数

输入变量e 和ec 的论域都设定为{－6，－5，－4，－3，－2，－1，0，1，2，3，4，5，6}，描述输入变量的词集为{负大，负中，负小，零，正小，正中，正大}，用英文字母开头缩写为{NB，NM，NS，Z，PS，PM，PB};本文设计的模糊PID控制器的输出为ΔKp，ΔKi 和ΔKd，它们的论域设定为{0，1，2，3，4，5，6}，描述输出变量的词集为{零，小，中，大}，用字母表示为{Z，S，M，B}。输入和输出均采用三角形隶属度函数，如图2 和图3 所示:

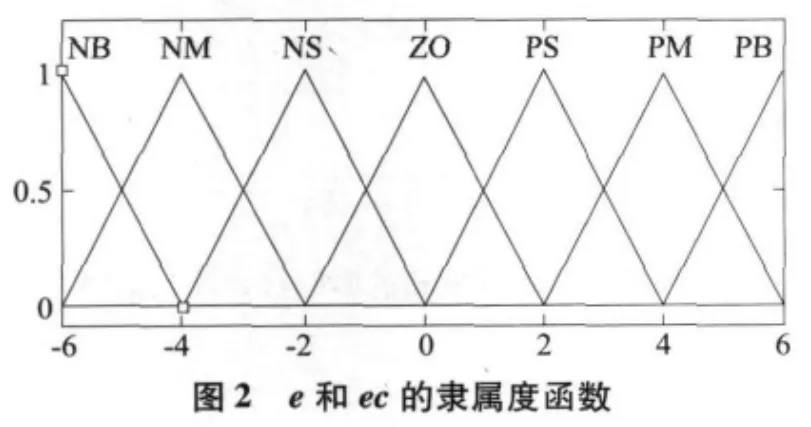
2.3 模糊规则的确定［4-5］

1)比例环节成比例的反映控制系统的误差信号，Kp的值增加会使得闭环系统的超调量增加，响应速度加快，控制时间加长，稳态误差减小，但不能完全消除稳态误差，Kp 过大会使系统的稳定性变差或使系统变得不稳定。

2)积分环节可以消除静态误差，提高系统的无差度，随着Ki 的值减小，可以减小系统的超调量，但响应速度减慢，Ki 的值太大会使系统变得不稳定。

3)微分环节反映偏差信号的变化趋势，可以在偏差信号变得太大之前，在系统引入一个有效的早期修正信号，随着Kd 的值增大系统的响应速度变慢，系统响应的超调量增加。

b)根据上述各个环节参数对系统的影响归纳出PID参数整定规则如下:

1)当偏差较大时，系统输出趋向稳态值的速度应越快越好，为保持系统较好的跟踪性，Kp 应取较大的值，而Kd 应取较小值。同时为避免系统响应出现较大的超调量，应限制积分作用，通常取Ki=0;

2)当偏差和偏差的变化率中等大小时，为使系统具有较小的超调，Kp 应取的较小一些，这种情况下，Kd 对系统的影响作用较大，应取较小值，而Ki 取值应适当;

3)当偏差较小时，为了使系统具有较好的稳定性，Kp与Ki 均应取的较大一些。同时为避免系统在设定值出现振荡，并考虑到抗干扰性能，当误差偏差率较大时，Kd 可取得较小一些;当误差变化率较大时，Kd 可取较大一些。

根据上述参数整定原则，可得出输出变量的控制规则表如下(表1，表2，表3):

表1 ΔKp 的模糊控制规则表

表2 ΔKi 的模糊控制规则表

表3 ΔKd 的模糊控制规则表

2.4 量化因子和比例因子的确定

模糊控制器的两个输入为误差E 和误差的变化EC，当采用模糊算法进行控制时，应先把输入量进行模糊化处理，使其从基本论域转换到相应的模糊集论域，即将输入变量乘以相应的量化因子。取E 的基本论域为［－1，1］，EC 的基本论域为［－8.5，8.5］，E 和EC 的量化因子分别为Ke=6/1=6，Kci=6/8.5=0.7。每次采样模糊控制算法给出的控制量需经过去模糊才作用于被控对象，即乘以相应的比例因子，取Kp，Ki，Kd 的基本论域分别为［0，60］，［0，6］，［0，24］;则比例因子分别为KKp=60/6=10，KKi=0.6/6=0 .1，KKd=24/6=4。

3 仿真研究

仿真参数设定:同步发电机的参数设定为Td=6 s，KG=1;移相触发单元和功率放大单元的参数设定为TZ=0.3 s，KZ=1;电压测量比较单元的参数设定为TR=0.02 s，KR=1。常规PID 控制器的参数设定为:Kp=120，Ki=9，Kd=10。

在simulink 中对所设计的模糊PID 励磁控制器进行仿真研究，仿真模型如图4 所示:

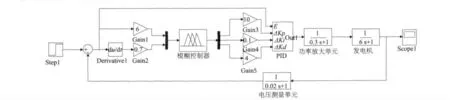
图4 模糊PID 励磁控制器的仿真模型

1)初始时刻给系统一个幅值为1 的阶跃信号，比较常规PID 控制和模糊PID 控制阶跃响应曲线，结果如图5所示。可以看出模糊PID 励磁控制基本没有超调量，且调节时间只有约0.3 s，在调节精度和快速性方面有更好的控制效果。

图5 两种励磁控制器的阶跃响应曲线

2)为模仿发电机的抗干扰能力，在5 s 时对系统加入幅值为0.15 的正向阶跃扰动信号，在8 s 对系统加入幅值为0.15的负向阶跃扰动信号，两种控制方式的扰动响应曲线如图6 所示。模糊PID 励磁控制的干扰调节时间约为0.2 s，抗干扰能力优于常规PID 控制器，具有较强的鲁棒性。

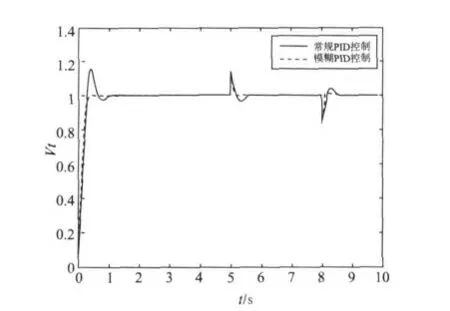
图6 两种励磁控制器的阶跃扰动响应曲线

4 结论

通过simulink 对励磁系统的仿真结果表明，模糊自适应PID 励磁控制器具有较好的控制效果，它调节速度快，超调量小，抗干扰能力强，能够满足同步发电机稳态、暂态稳定性要求。随着电力系统逐步向高压、超高压发展，对其稳定性的要求必将越来越高，研究设计能够满足更高稳定性要求的励磁控制器具有重要意义。把模糊控制和常规PID 相结合的励磁控制方式在实际应用中具有一定的推广价值。

［1］杨冠城.电力系统自动装置原理［M］.4 版.北京:中国电力出版社，2007.

［2］李士勇.模糊控制·神经控制和智能理论控制论［M］.哈尔滨:哈尔滨工业大学出版社，1998.

［3］魏巍.MATLAB 控制工程工具箱技术手册［M］.北京:国防工业出版社，2004.

［4］陶永华，尹怡欣，葛芦生.新型PID 控制及其应用［M］.北京:机械工业出版社，1998.

［5］张立峰，金秀章，田沛.基于模糊自调整PID 技术的励磁控制器研究［J］.华北电力大学学报:2006，33(4):20－22.