一种基于区间直觉模糊集的多属性决策方法
2013-04-07孙小慧1b白礼虎
孙小慧,吴 涛,1b,孙 恒,白礼虎
(1.安徽大学a.数学科学学院;b.计算智能与信号处理教育部重点实验室,安徽合肥230039;2.北京林业大学水土保持学院,北京100083)
0 引言
自从Zadeh在1965年创立模糊集理论以来[1],模糊集理论及其应用方法得到不断的完善和发展。Atanassov同时考虑隶属度、非隶属度和犹豫度三方面的信息,于1986年提出了直觉模糊集的概念[2],与Zadeh的模糊集相比,直觉模糊集在处理模糊性和不确定性等方面更具灵活性和实用性。1989年文献[3]对直觉模糊集进行了拓展,提出区间直觉模糊集。
近年来,一些学者对区间直觉模糊集的理论进行了研究,文献[4]给出区间直觉模糊集的一些基本运算和它们的基本性质;文献[5]定义了区间直觉模糊集的关联度,并给出区间直觉模糊集关联性的两个分解定理。更多的学者研究区间直觉模糊集理论在多属性决策中的应用:文献[6]定义了区间直觉模糊集的得分函数和精确函数,基于这两种函数给出了区间直觉模糊集的一种排序方法;文献[7]对文献[6]的方法进行了改进,提出新的精确函数,并将其应用于决策问题;文献[8]考虑到区间直觉模糊集的犹豫度对决策方案的影响,分析了文献[6-7]所定义精确函数的缺陷,对其进行改进,提出了一种新的精确函数,并应用于多属性决策问题。随后,文献[9]提出了一种新的得分函数并给出相应的性质。
虽然这些方法在决策问题中得到了一定程度的应用,但目前所有的得分函数和精确函数都有自己的不足之处,对一些问题无法做出决策。本文通过分析区间直觉模糊集的隶属度、非隶属度对犹豫度的影响和这三方面对决策方案的影响,对已有的精确函数和得分函数进行修正和改进,定义了一种基于区间直觉模糊集的得分函数,并将其应用于多属性决策问题。
1 预备知识
设X是一个非空集合,则称A={〈x,μA(x),vA(x)x∈X}为直觉模糊集,其中,μA(x)∈[0,1]和γA(x)∈[0,1]分别为集合X中元素x属于A的隶属度和非隶属度,且满足0≤μA(x)+γA(x)≤1,∀x∈X。
若μA(x),γA(x)是区间数,即


x属于A的犹豫度为:


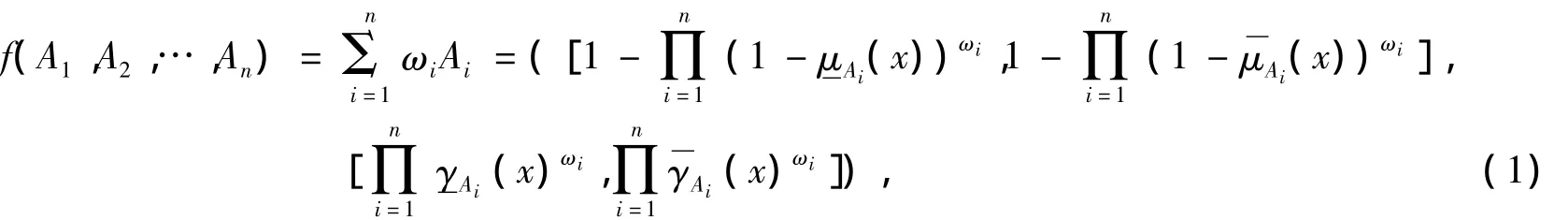
其中,ωi∈[0,1]为Ai(i=1,2,…,n)的权重;ωi=1。
特别地,若ω1=ω2=ω3=…=ωn=,则称f为区间直觉模糊数的算数平均算子。


其中,ωi∈[0,1]为Ai(i=1,2,…,n)的权重;ωi=1。
得分函数和精确函数都为一种评价准则,但考虑的方向不一样,得分函数类似于统计学中的均值,而精确函数类似于统计学中的方差。相同的是,在决策问题中若某一方案的得分函数值或精确函数值越大,对应的决策方案越优。以下是几种已有的得分函数和精确函数。
定义3[6]设A=([a,b],[c,d])为一个区间直觉模糊数,则称△(A)=为A的得分函数,其中,△(A)∈[-1,1]。
定义4[6]设A=([a,b],[c,d])为一个区间直觉模糊数,则称H(A)=为A的精确函数,其中,H(A)∈[0,1]。
定义5[7]设A=([a,b],[c,d])为一个区间直觉模糊数,则称
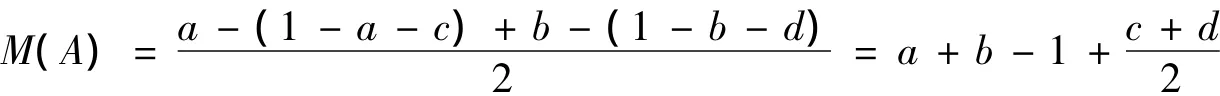
为A的精确函数,其中,M(A)∈[0,1]。
定义6[8]设A=([a,b],[c,d])为一个区间直觉模糊数,则称

为A的精确函数,其中,S(A)∈[0,1]。
定义7[9]设A=([a,b],[c,d])为一个区间直觉模糊数,则称

为A的精确函数,其中,L(A)∈[-1,1]。
2 得分函数的改进
若两个决策方案分别为A1=([0.2,0.5],[0.1,0.4]),A2=([0.3,0.4],[0.2,0.3]),则

由定义3所给的得分函数和定义4、定义5所给的精确函数,所得到的两种方案的结果都是相等的,即两种方案未得到排序。
若两个决策方案分别为A3=([0,0.2],[0.1,0.2]),A4=([0.1,0.2],[0.3,0.6]),则S(A1)=S(A2)=0.25。
定义6所给的精确函数对于此决策方案也得不到有效的排序。
若两个决策方案分别为A5=([0.3,0.4],[0,0.1]),A6=([0.2,0.6],[0,0.4]),则L(A1)=L(A2)=0.32。
定义7所给的精确函数对于此决策方案也无法做出判断。
为解决以往得分函数和精确函数的缺陷和不足,考虑到区间直觉模糊集中隶属度和非隶属度对犹豫度的影响,定义了一种新的得分函数。
定义8 设A=([a,b],[c,d])为一个区间直觉模糊数,则称
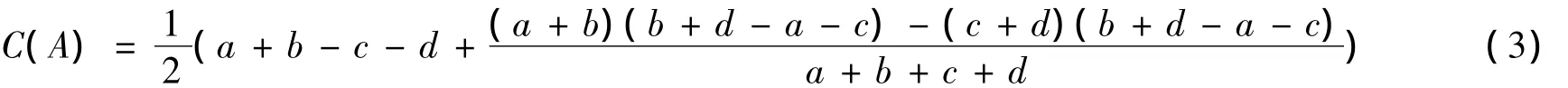
为A的得分函数,其中C(A)∈[-1,1]。
性质1 设A=([a,b],[c,d])为一个区间直觉模糊数,
(Ⅰ)若A=([1,1],[0,0]),则C(A)=1。
(Ⅱ)若a+b=c+d或a=c,则C(A)=0。
(Ⅲ)若A=([0,0],[1,1]),则C(A)=-1。
若一个区间直觉模糊数A=([a,b],[c,d])对应于上述性质中的情形(Ⅱ),可以通过文献[6]中定义的精确函数进行排序。
对于方案
A1=([0.2,0.5],[0.1,0.4])与A2=([0.3,0.4],[0.2,0.3]),
A3=([0,0.2],[0.1,0.2])与A4=([0.1,0.2],[0.3,0.6]),
A5=([0.3,0.4],[0,0.1])与A6=([0.2,0.6],[0,0.4]),
运用定义8所给出的得分函数计算可得C(A1)=0.05,C(A2)=0.08,可得C(A2)>C(A1),所以方案2优于方案1;C(A3)=-0.02,C(A4)=-0.20,可得C(A3)>C(A4),所以方案3优于方案4;C(A5)= 0.225 0,C(A6)=0.062 5,可得C(A5)>C(A6),所以方案5优于方案6。
3 基于区间直觉模糊集的多属性决策
首先给出基于区间直觉模糊集多属性决策的算法步骤:
步骤1,运用式(1)或式(2)对各个方案的属性进行集成;
步骤2,通过式(3)对集成后的各个方案进行得分计算;
步骤3,对得分进行排序,得分最高者为最优方案。
为说明本文所定义的得分函数是有效的,采用文献[8]中的实例进行分析,具体实例如下:设某一决策问题有4个候选方案Ai,i=1,2,3,4和3个评价指标Ej,j=1,2,3,各个指标的权重分别为0.35,0.25,0.40。各候选方案在各指标下的特性用区间直觉模糊数表示如下,试选取最优方案。


运用加权算术平均算子(1)对各个方案的各个属性进行集成,从而得到各个方案的综合区间直觉模糊值αi(i=1,2,3,4)为:

通过定义8所定义的得分函数,计算各个方案的得分为:

可得C(α3)>C(α4)>C(α1)>C(α2),所以方案排序为A3>A4>A1>A2,即第4个方案为最优方案。排序结果与文献[8]的排序结果是完全一致的,说明本文所给得分函数是可行的。
4 结束语
本文首先分析了现有的5种基于区间直觉模糊集得分函数和精确函数的缺点与不足,充分考虑到区间直觉模糊集的特点,定义了一种新的得分函数,并给出了基于此得分函数的区间直觉模糊集的多属性决策算法,最后给出了实例分析,实例证明本文所定义的得分函数是有效的。
[1] Zadeh L A.Fuzzy Sets[J].Information and Control,1965,8(3):338-353.
[2] Atanassov K.Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.
[3] Atanassov K,Gargov G.Interval-valued Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1989,31(3):343-349.
[4] Atanassov K.Operators Over Interval-valued Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1994,64(2):159-174.
[5] Bustibce H,Burillo P.Correlation of Interval-valued Intuitionistic Fuzzy Sets[J].Information Sciences,2002,144(1/4): 219-225.
[6] 徐泽水.区间直觉模糊集信息的集成方法及其在决策中的应用[J].控制与决策,2007,22(2):215-219.
[7] Jun Y.Multicriteria Fuzzy Decision-making Method Based on a Novel Accuracy Function Under Interval-valued Intuitionistic Fuzzy Environment[J].Expert Systems with Applications,2009,36(3):6899-6902.
[8] 要瑞璞,沈惠璋.区间直觉模糊集多属性决策方法[J].数学的实践与认识,2011,41(18):135-138.
[9] Lakshmana G N V,Muralikrishnan S,Sivaraman G.Multi-criteria Decision-making Method Based on Interval-valued Intuitionistic Fuzzy Sets[J].Expert Systems with Applications,2011,38(3):1464-1467.
