Bancroft算法用于坐标初值计算
2013-04-07王修益
华 慧,田 力,杨 伟,王修益
(1.上海市静安区房地产测绘中心,上海 200040;2.测绘出版社,北京 100045;3.成都国腾电子集团有限公司,四川成都 610041)
一、前 言
对于地面固定站,测站的近似坐标可以较为精确地获取,但是对于动态的测站,如高速运动的飞机,一般很难精确地知道每个观测历元的近似坐标。获取近似坐标一般采用迭代的方法,即不采用任何的坐标信息,而是通过反复迭代得到精确的坐标。但是有时候迭代搜索的收敛速度较慢,时间较长,甚至在有些情况下迭代不一定收敛[1]。另外,在采用GPS进行低轨卫星实时定轨中,也对计算速度有更高的要求。在这些要求下快速获取定位初值有助于数据处理的快速精确进行。针对这种情况,本文介绍Bancroft算法,并将其应用于低轨卫星初轨计算,结果显示该算法简单有效。
二、Bancroft算法
考虑误差因素,对于卫星j,伪距观测值的无电离层影响线性组合P定义如下[2]



式中,Pj已经对 GPS钟差进行了改正;xj、yj、zj为第j颗GPS卫星的坐标。定义b=cδ,将式(2)重新写为
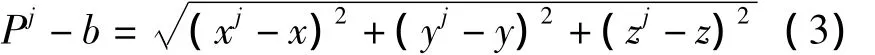
对式(3)平方得到

对式(4)进行整理得到
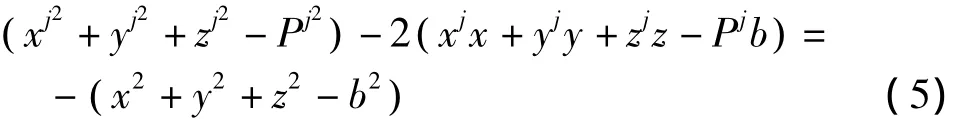
定义 Lorentz内积为[2]

根据式(6)的定义,将式(5)写为

式中,rj为GPS卫星的坐标矢量;r为测站的坐标矢量。对于每一颗卫星的伪距观测值,都能建立以上方程。式中待求参数为坐标矢量r与钟差参数b,从理论上来讲,只要有4颗卫星就能够求解。定义

则对于4颗卫星的伪距观测方程写为
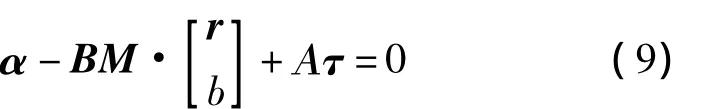
式中,α为4×1的向量,其分量为
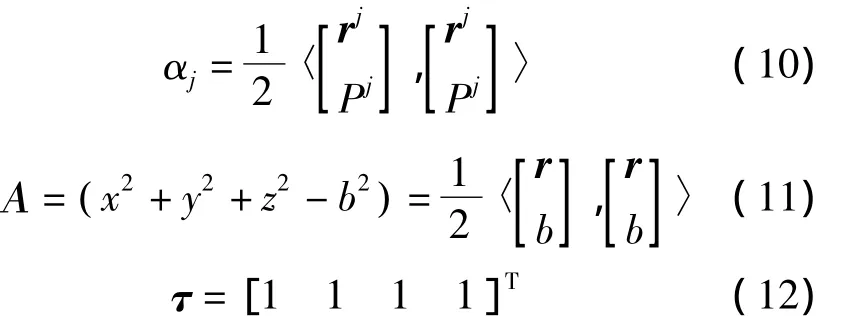

将式(13)代入式(9)有
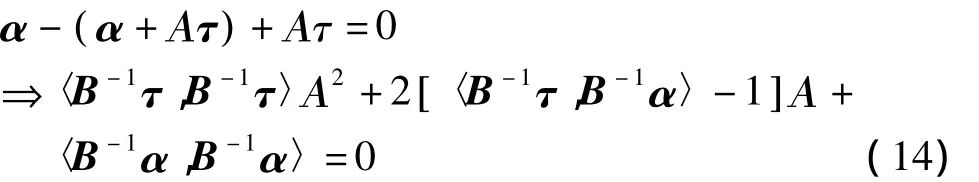
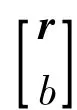
上面介绍的是基于4颗GPS卫星的解,但是实际上大部分情况下观测到的卫星会多于4颗,设实际观测到的卫星个数为n,则式(9)中
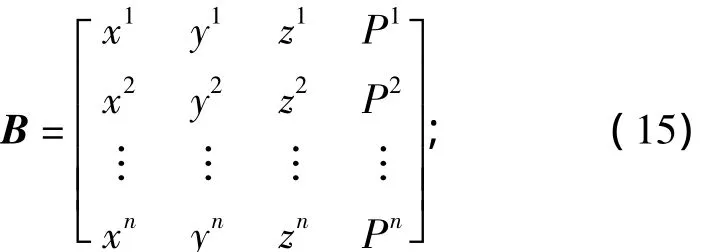
α为n×1的向量;τ为n×1的向量(每个元素都是1)。此时由于B不是方阵,不能直接求逆。此时将式(9)写为

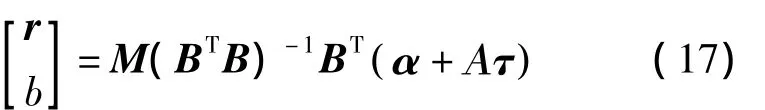
按照与式(14)同样的计算方法,可以得到式(16)中Α的解为
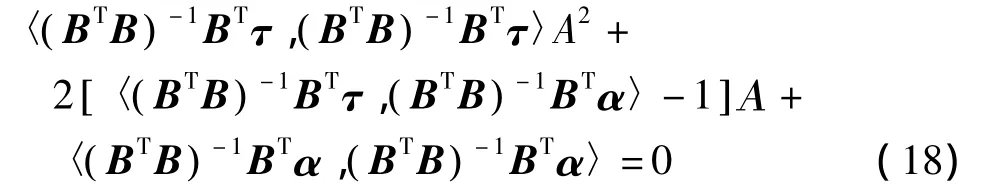
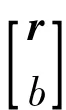
采用上述Bancroft算法,计算量小,而且不需要迭代。但是由于无法知道测站坐标的初值,因而与坐标有关的各种改正(对流层、相对论效应等)无法求得。值得一提的是,不采用这些改正得到的近似坐标即能够满足近似坐标的精度要求。如果需要更为精确的近似坐标,可以在求得概略坐标之后,考虑各种改正,再次采用该算法进行计算。此时的迭代比没有任何信息所进行的迭代,已经减少了很多的计算量。因而采用该算法能够大大提高计算速度。并且,由于计算过程中不涉及任何矩阵求逆计算,因而该算法不存在发散的问题。
三、卫星初轨计算
CHAMP卫星距离地面几百千米,其运动速度远大于地面载体(>7 km/s),卫星上搭载了GPS接收机,用于动态定位。与地面测站一致,CHAMP卫星的GPS观测值也提供了标准的RINEX格式文件。为验证该算法的有效性,本文对CHAMP卫星2004年191的星载GPS观测数据进行了分析。图1表示采用Bancroft算法与采用最小二乘解迭代求解得到轨道之间的差值,其中最小二乘解轨道相对参考精密轨道[3],差值的 RMS 为 1.21 m,该精度与CHAMP卫星伪距观测量的精度相当。从图1可以发现,除少数跳跃点外,Bancroft算法与最小二乘解的差别在分米级,这也说明采用Bancroft算法得到的轨道近似值精度已经在伪距定位的精度范围之内。

图1 Bancroft算法与最小二乘解的差值注:为便于区分,X方向加了2 m;Z方向减了2 m。
四、结束语
从公式的推导中可以看出,采用Bancroft算法计算简单,无需迭代,运算量少。从计算中也可以看出,采用伪距观测量时该算法得到的轨道初值的精度与最小二乘迭代的结果相当。另外,除了应用卫星轨道初值计算外,该算法还可以应用于所有测距定位中的近似坐标计算(如GPS动态定位、传统测边网等)。
[1] 崔书珍,彭军还,谢勋峰.未知点初始坐标精度对基线解算结果的影响——Bernese和GAMIT解算结果对比[J].桂林工学院学报,2006,26(2):218-220.
[2] TEUNISSEN P J G,KLEUSBERG A.GPS for Geodesy[M].Berlin,Heiddberg,New York:Springer-Verlag,1998.
[3] CHEN Junping,WANG Jiexian.Reduced-dynamic Precise Orbit Determination for Low Earth Orbiters Based on Helmert Transformation[J].Artificial Satellite,2008,42(3):155-165.
