机载小光斑全波形LiDAR数据处理及应用
2013-04-07周静平张爱武王书民
周静平,张爱武,王书民
(首都师范大学三维信息获取与应用教育部重点实验室,北京 100048)
一、引 言
机载激光雷达(airborne laser scanning,ALS)也指雷达或激光雷达,是一种通过激光器向地表发射红外线短波脉冲,并由光电接收器接收背向散射的回波信号的主动式光学遥感器[1]。作为一种先进的新型对地观测系统,它集激光、全球定位系统和惯性导航系统(inertial navigation system,INS)3项技术于一身,并用于快速获取地面目标的三维空间信息。
自20世纪70年代美国、加拿大率先研制航空激光雷达测量系统以来,此项技术发展特别迅速[2]。20世纪80年代开始出现一些试验系统,到90年代中后期逐渐成熟。尤其是20世纪90年代中期商业ALS产品和服务制造商的出现,使得激光雷达系统和存储技术得到了前所未有的迅猛发展。2004年,奥地利Riegl公司推出了世界上第一台商业机载小光斑全波形激光雷达数字测量系统。随之,Optech ALTM 3100E、TopEye Mark II、Leica ALSII等机载激光雷达系统也均可进行全波形数字化测量,并在地形测绘、林业、环境监测、三维城市建模等许多领域得到了广泛的应用[3]。
二、全波形LiDAR理论
1.激光传感器
激光雷达的工作原理与传统雷达遥感大体相同。激光测距系统是其核心组成部分,以激光波束扫描的方式测量激光器到目标方向激光照射点的距离,即通过测量地面点的回波脉冲与激光的发射脉冲之间的时间延迟得到激光器到地面点之间的距离[4]。测距原理公式为

式中,R为激光器到目标物的距离;c为光速;t为激光脉冲从激光器到目标物传输的往返时间[5]。机载激光雷达系统的R和t是可以相互转换的,具体使用哪个可根据实际需求进行选择。激光雷达的测量方式是十分精确的,其测量精度常常可达到毫米级。再结合GPS记录的坐标信息和INS记录的姿态角信息,通过联合解算便可得到激光点的大地坐标。
2.全波形激光雷达
全波形LiDAR即全数字波形激光雷达,采用数字化方式,不仅记录若干次离散回波信号,而且将发射信号和回波信号均以很小的采样间隔进行采样并记录[6-8]。激光雷达记录的回波波形是对光斑内各个点的反射信号按时间先后顺序的记录,回波波形代表了激光后向散射的能量,也就是说,回波波形可以看做是回波强度信息在接收时间轴上的一个函数。
较之传统的LiDAR,全波形LiDAR具有3个方面的优点[7]:① 通过对接收的回波信号进行处理,可以提取出所有的脉冲回波信息,也就是说同一激光束中,全波形LiDAR系统比传统LiDAR系统能提供更详细的点云信息(特别是在林木覆盖区域),且密度大,层次感强;②通过对回波进行波形分解、拟合,能得到更加精确的电云坐标;③ 对接收到的波形信号进行处理、建模,通过模型可得到更加丰富的地物特征。全波形LiDAR对波形信号进行了精确细致的存储和刻画,尤其是对于树木等特殊地物,它能提供更多的目标信息。
3.雷达方程
结合传统雷达方程,激光雷达方程可表示如下[1]

式中,Pr是接收的能量;Pt是发射脉冲能量;Dr为接收器孔径大小;R是目标与飞行器的距离;βt为发散角;ηsys表示系统衰减系数;ηatm表示大气的衰减系数;σ被称为背向散射截面(back scatter cross section)。很显然,式(2)是在理想状况下的一个简单散射体的散射能量方程,对于一个光斑内存在多个目标物的复杂散射体,其反射的能量组成将更为复杂,仍需进一步研究。
波形通常被模型化为一系列高斯脉冲。根据下面公式进行推算,最终得到接收的能量Pr被表示为[1]
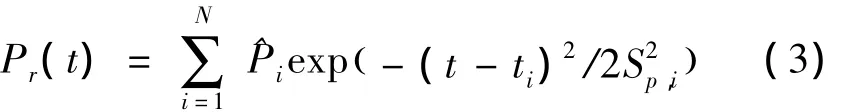
式中,ti为往返的时间;为目标i的振幅;Sp,i为回波脉冲的标准差。

式中,Ss是发射脉冲的标准差;为发射脉冲的振幅;Si是目标i回波的标准差;σi为目标i总的后向散射截面,是目标地物不同散射截面的积分。目标的散射截面与地表的粗糙度有关,可根据发射脉冲信号与不同目标的后向散射截面的积分得到一个接收的波形。
对全波形数据进行处理时,通常还要进行辐射校正。本文采用的是Riegl LMS-Q560数据,经过分析比较后决定采用Wolfgang Wagner所提出的利用柏油路面(反射率为0.2)作为标准参考的方法,具体校正公式为[9]

三、波形分解方法和步骤
1.分解方法
波形分析技术最先由美国宇航局(NASA)用于其机载大光斑LiDAR系统上,激光雷达波形数据分析也是以美国为首进行发展的。目前,对机载激光全波形数据进行分解,国外研究得较早也较为深入,国内研究最近几年也逐渐开始。
目前波形数据的处理方法主要有3种:①阈值法 (average square difference function[10],ASDF);②反卷积法;③波形分解法。
波形分解的方法是将回波的波形看作是一个光斑内不同高度的目标物对激光脉冲反射后综合作用[11]的结果,其将不同高度处的目标物回波从接收的波形信号中提取出来,从而达到对目标进行定位和识别的目的。波形分解的核心内容包括噪声提取和目标物反射回波波形的准确定义。目前波形分解的研究都是基于对回波理想情况下的模拟,多采用高斯函数或者正态分布函数近似刻画单个目标的回波波形。其中,采用高斯函数的形式是目前采用较多也是较为准确的一种方法。Wagner[12]等最先采用了高斯分解的方法对第一个能够记录完整波形小光斑激光雷达Riegl LMS-Q560的数据进行了处理,结果证明98%以上的回波数据可以用高斯函数很好地拟合,其精度也能够达到规定的要求。目前,有几种方法可以实现高斯分解,如Wagner等开发的基于非线性最小二乘的分层高斯函数波形拟合法;Jutzi等实现的高斯-牛顿法;Persson等的 EM(Expectation-Maximization)[13]算法实现;武汉大学的马洪超、李奇[14]采用改进的EM算法的波形分析技术;De Boor和Cox分别提出的递推定义的B样条法等。波形分解是目前机载激光雷达[15-16]较为常用的波形数据处理算法,均可获得较为理想的结果,并可获取更多的额外参数。
本文采用基于高斯数学模型的波形分解法,对研究区波形数据进行波形分解和拟合,采用L-M算法[1]并利用最小二乘法原理不断迭代优化,最终得到最优的参数,即每个单个波形的振幅、距离、波宽。
2.分解步骤
1)数据预处理(波形数据读取、噪声去除、波形平滑)。
2)参数初始化(峰值点检测与初始参数估计)。
3)参数提取(依据拟合函数和分解算法)。
四、试验成果和分析
本文的研究区位于河北省城区,该区域内地物类型丰富,有人工建筑物、道路、高大树木、低矮灌木、草地等。经过对研究区机载小光斑全波形Li-DAR数据进行波形分解,得到了5 481 859条波形数据。为了直观地显示及后续处理的方便,本文在Matlab平台上,制作出了波形数据的显示界面,如图1所示。

图1 波形显示界面
利用此界面,可对本研究区域所有的波形数据逐条地进行直观的显示,也为后期的数据处理提供了很多便利。研究区具有丰富的地物类型,所得的数据回波信息也很丰富,回波次数最多可达7次,详细情况见表1。
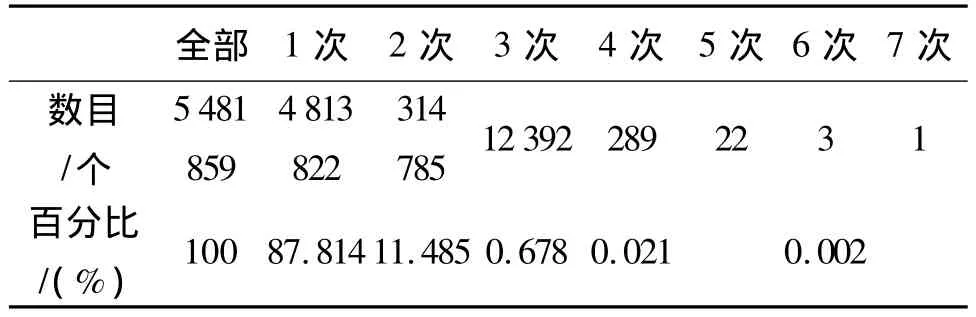
表1 回波数目分布情况
在Matlab平台上,对研究区全波形数据进行了显示,并且利用激光点云数据处理专业软件Terrasolid对点云数据进行了大致分类(见表2)。由于研究区域较大,为了方便显示,只截取了其中一部分,效果如图2所示。

表2 分类情况
从表1和图1可以明显看出,研究区的回波次数最多为7次,最少为1次。大部分为1次回波占87.814%;2次以上回波仅占12.186%。这是因为研究区位于城区,虽然地物类型较为丰富,但因建筑用地(房屋建筑、道路等)面积占据了大部分(占86.92%),这些地区较为平坦,激光对其无穿透;此研究区有也较多高大树木、低矮灌木等(占13.08%),林木等地物具有叶间、枝间缝隙,激光可穿透。对比地物分类图,可以明显看出,建筑用地及道路等非植被区域和一次回波区大致重合,仅有1次回波;而有林木分布的植被区域和多次回波区大致吻合,回波为多次。整体上,也可以从表1和表2中1次回波的百分比和非植被区的百分比大致相同,多次回波的总百分比和植被区的百分比大致相等来进一步得到说明。值得注意的是,研究区还有部分回波为0,这是因为地物反射波的方向不在激光接收器的视域内,导致接收不到地物的回波信息,或者是地物的反射率太低所致。

图2 回波次数及地物分类图
另外,第一次回波反映的是建筑物轮廓信息和高大灌木的冠层,可用于道路信息、建筑物的轮廓信息提取,也可用于计算高大灌木的植株高度信息;其他次回波反映的是林木信息,可用于计算林木的蓄积量;最后一次回波反映的是地面,可用于辅助地形图和数字高程模型制作。
经过波形分解,提取出了回波脉冲的距离、振幅和波宽等参数信息,结合点云分类信息,所成图件如图3所示。
研究区波形数据所提取的参数信息中,距离参数指的是地物与激光发射器之间的距离,间接反映了高程上的差异,传统的分类有很多都是基于高程进行的;振幅参数与地物类型间关系最为紧密,反映也最为直接;波宽参数与植被间关系较为紧密。该研究区所提取出的波形数据,振幅最大值为0.844 3 m,最小值为0.000 137 m,大多分布在0.06 m以下(即0 m~0.01 m),如图4所示;波宽最大值为214 nm,最小值为14 nm,大多分布在150 nm以下。

图3 回波参数及分类图
值得说明的是,距离、振幅、波宽信息只是波形的单一参数,若仅仅用它进行分类,效果并不十分理想。由图3可知,植被对波宽参数比较敏感,并且随着树木高度的增加,其波宽也随之增大。如高大树木比低矮草地的波宽要宽;高大建筑物和树木冠层对距离信息比较敏感。上述距离、振幅、波宽是波形数据的重要参数信息,可以为后期点云精分类和数据的深入应用提供可靠依据。因此,这些参数信息的提取是十分重要和必要的。
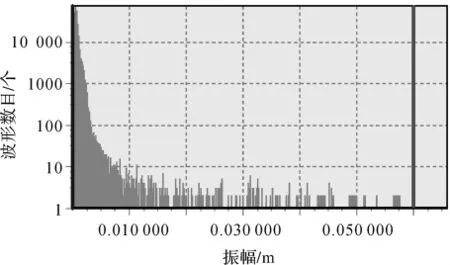
图4 振幅分布图
五、结论与展望
本文以高斯函数波形分解理论为依据,对研究区的机载小光斑全波形LiDAR数据进行了波形处理,提取出了各个波形的振幅、距离、波宽等参数,这些特征对后续的地物分类提供了科学依据。通过试验,充分验证了利用高斯模型函数来拟合机载小光斑全波形脉冲是切实可行的,并在Matlab平台上开发出了机载小光斑全波形数据显示界面,可方便直观地显示所想查看的各条波形信息。有效波形的提取是波形分析领域里的一个难点问题。此外,背向散射体截面是一个很主要的参数,它包含了不同地物的距离特征和散射特征,这个参数对点云的分类指导意义特别重大。如何对机载小光斑全波形数据进行有效的波形分解和如何充分利用分解后提取出的参数信息对地物进行分类,将是进一步研究的内容。
机载小光斑全波形数据具有能够快速获取地表物体的精确三维空间信息和很多的地物特征信息的优势,未来还将继续在地形测绘、农林业、数字城市建设等诸多领域得到越来越广泛和深入的应用。
[1] WOLFGANG W.Gaussian Decomposition and Calibration of a Novel Small-footprint Full-waveform Digitizing Airborne Laser Scanner[J].ISPRS Journal of Photogrammetry & Remote Sensing,2006,60:100-112.
[2] ACKERMANN F.Airborne Laser Scanning-Present Status and Future Expectations[J].ISPRS Journal of Photogrammetry & Remote Sensing,1999,54(2-3):64-67.
[3] 王成,MENENTI M.机载激光雷达数据的误差分析及校正[J].遥感学报,2007,11(3):390-397.
[4] BACHMAN C G.Laser Radar Systems and Techniques[M].London:Artech House,1979.
[5] BALTSAVIAS E P.Airborne Laser Scanning:Basic Relations and Formulas[J].ISPRS Journal of Photogrammetry and Remote Sensing,1999,54(2-3):199-214.
[6] HOFTON M A,MINSTER J B,BLAIR J B.Decomposition of Laser Altimeter Waveforms[J].IEEE Transactions on Geoscience and Remote Sensing,2000,38(4),1989-1996.
[7] HUG C.A Waveform Digitizing LiDAR Terrain and Vegetation Mapping System[J].International Archives of Photogrammetry,Remote Sensing and Spatial Information Sciences(Freiburg,Germany),2004(36):24-29.
[8] PERSSON Á,SÖDERMAN U,TÖPEL J,et al.Visualization and Analysis of Full-waveform Airborne Laser Scanner Data[J].International Archives of Photogrammetry,Remote Sensing and Spatial Information Sciences,2005(36):103-108.
[9] WAGNER W,RONCAT A,MELZER T,et al.Waveform Analysis Techniques in Airborne Laser Scanning.[J] International Archives of Photogrammetry,Remote Sensing and SpatialInformation Sciences,2007,36:413-418.
[10] RONCAT A,WAGNER W,MELZER T,et al.Echo Detection and Localization in Fullwaveform Airborne Laser Scanner Data Using the Averaged Square Difference Function Estimator[J].The Photogrammetric Journal of Finnland,2008,21(1):62-75.
[11] JUTZI B,STILLA U.Range Determination with Waveform Recording Laser Systems Using a Wiener Filter[J].ISPRS JPRS,2006,61(2):95-107.
[12] WAGNER W,ULLRICH A,MELZER T,et al.From Single-Pulse to Full-Waveform Airborne Laser Scanners:Potential and Practical Challenges[C]∥Proceedings of International Society for Photogrammetry and Remote Sensing XXth Congress:XXXV.[S.l.]:ISPRS,2004.
[13] DEMPSTER A P,LAIRD N M,RUBIN D B.Maximum Likelihood from Incomplete Data via the EM Algorithm[J].J Royal Stat Soc Ser B-Methodol,1977,39:1-38.
[14] 马洪超,李奇.改进的EM模型及其在激光雷达全波形数据分解中的应用[J].遥感学报,2009,13:35-41.
[15] SUN G,RANSON K J.Modeling LiDAR Returns from Forest Canopies[J].IEEE Trans Geosci Remote Sensing,2000,38:2617-2626.
[16] BALTSAVIAS E P.A Comparison between Photogrammetry and Laser Scanning[J].ISPRS Journal of Photogrammetry and Remote Sensing,1999,54(2/3):83-94.
