噪声相关情况下的卡尔曼滤波
2013-04-07赵长胜
测绘通报 2013年1期
赵长胜
(江苏师范大学测绘学院,江苏徐州 221113)
一、标准卡尔曼滤波
卡尔曼滤波是基于一组观测序列L1,L2,…,Lk及系统的动力学模型信息来求解状态向量估值的一种算法。卡尔曼滤波分别采用状态方程和观测方程来描述动力学模型和观测模型,设状态方程和观测方程为
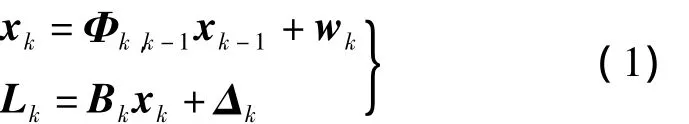
式中,xk-1、xk分别表示第k-1时刻和k时刻的状态向量;Φk,k-1称为状态转移矩阵;Lk为k时刻的观测向量;Bk为系数矩阵;wk、Δk分别为系统的动态噪声向量和观测噪声向量。
假设wk、Δk是零均值白噪声序列,且误差互不相关,即有

白噪声条件下的卡尔曼滤波状态预测值和协方差分别为
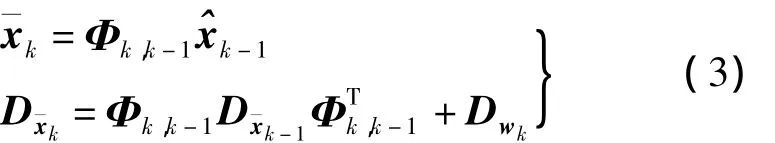
观测向量带来的新的信息(称为新息)及其协方差矩阵为

增益矩阵为

状态估计向量及其协方差矩阵为
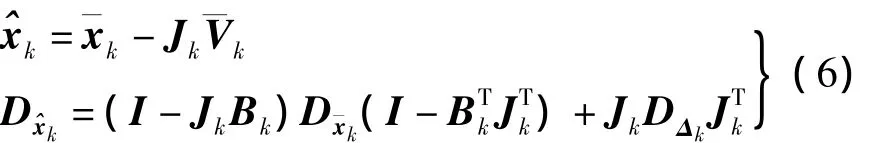
二、噪声互相关情况下卡尔曼滤波的最小二乘解
系统的动态噪声wk和观测噪声Δk虽然是高斯白噪声系列,但动态噪声与观测噪声相关,即在式(2)中

即


由式(1)中的观测方程可以列出观测值的误差方程


这时状态向量可用最小二乘原理获得直接解为
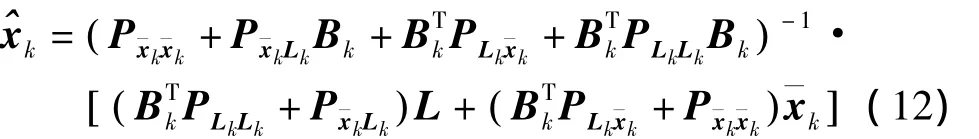
三、噪声互相关情况下卡尔曼滤波的相关变换解
所谓相关变换解,实际是将动力学模型预测向量与观测向量的互协方差阵转变为零。先将状态方程变为
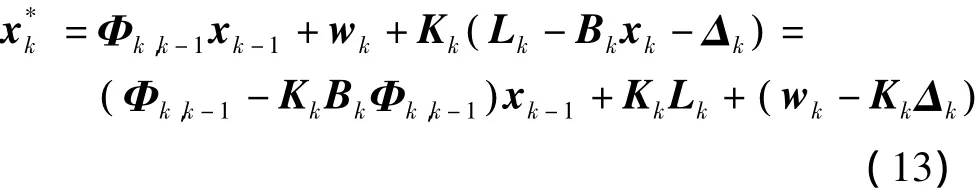
式中,Jk为待定矩阵。令
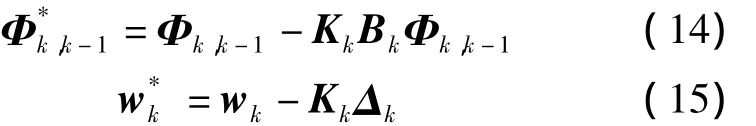
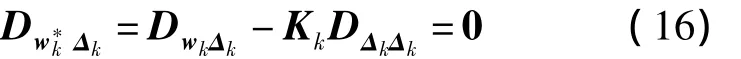
因此有

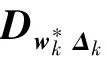
四、噪声互相关情况下卡尔曼滤波的改化解
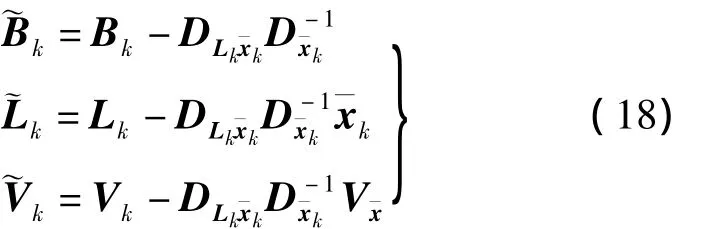
则误差方程变换为
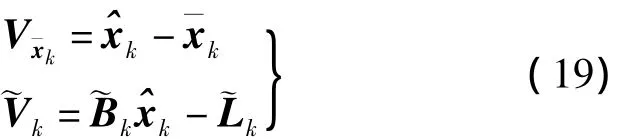
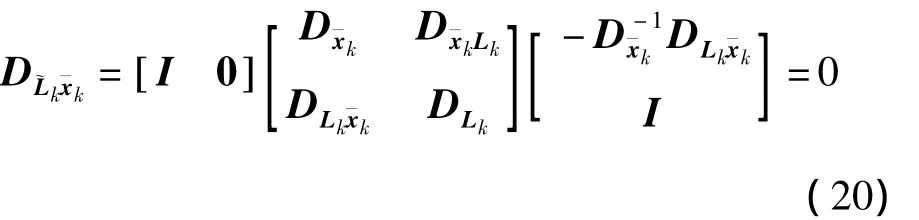
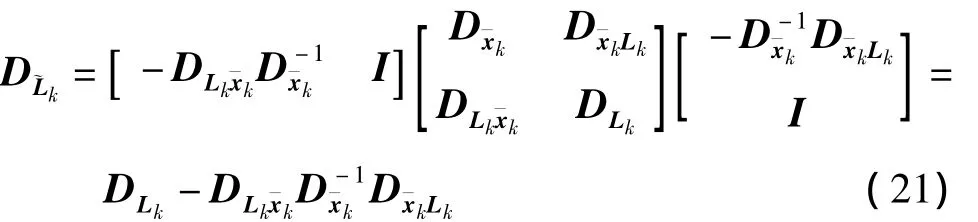

组成法方程并求逆得

由矩阵恒等变换可得
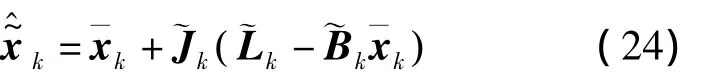
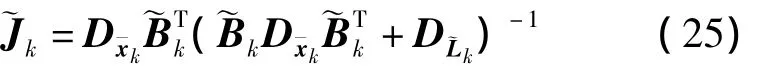
或由矩阵恒等式得

由式(24)经协方差传播律可得的协方差矩阵为

或为

[1] 杨元喜.自适应动态导航定位[M].北京:测绘出版社,2006.
[2] 赵长胜.有色噪声滤波理论与算法[M].北京:测绘出版社,2006.
[3] 盛梅,邹云.相关噪声系统的卡尔曼滤波[J].宇航计测技术,2003,23(4):38-42.
[4] 赵长胜,陶本藻.有色噪声作用下的卡尔曼滤波[J].武汉大学学报:信息科学版,2008,33(2):180-182.
