关于数字10的神奇特征（续十二）

王仲才

（南昌理工学院 江西 南昌 330044）

[引理1] 接连的10个正整数中，前5个取负，后5个取正，则它们的代数和是5的整数倍。

证明 设n为正整数，那么接连的10个正整数中，前5个是

前后对应之差都是5，代数和是45=5×9

证毕。

[引理2] 接连的10个正整数的2l次方中（l为正整数），前5个取负，后5个取正，则它们的代数和是5的整数倍。

证明 由[引理1]，l=0时结果成立，由2数平方差

得知，结论对于l=1时成立。

假设结论对于l=h（正整数）成立，即

是5的整数倍，那么，对于l=h+1时

由假设得悉，它是5的整数倍，总的代数和自然也是5的整数倍。

证毕。

[定理2] 接连的10个正整数的3l次方 （l为正整数）中，前5个取负，后5个取正，则它们的代数和是5的整数倍。

证明 由2数立方差公式

和[引理1]得悉，对应项之差都是5的整数倍，那么总的代数和自然是5的整数倍，即结论对l=1时成立。

假设l=h(正整数）时结论成立，即

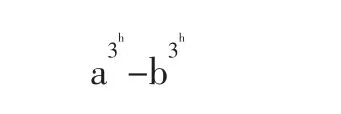
是5整数倍，那么对于l=h+1

由假设它是5的整数倍，那么总的代数和的自然数是5的整数倍。

证毕。

[定理3] 接连的10个正整数的5l次方 （l为正整数）中，前5个取负，后5个取正，则它们的代数和是5的整数倍。

证明 设n,m为正整数，则

它是5的整数倍。

由[引理1]和公式得知（上式取m=1)

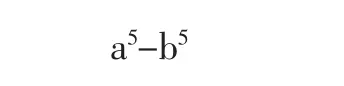
即对应项之差是5的整数倍，从而总的代数和自然是5的整数倍，即结论对5次方成立。

假设对于l=h（正整数）结论成立，即

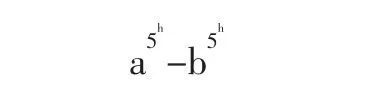
是5的整数倍，那么对于l=h+1

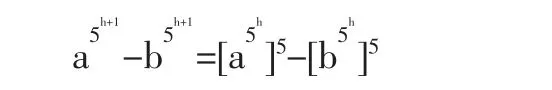
是（1）式和假设，它也是5的整数倍，从而总的代数和是5的整数倍。

证毕。

[定理4] 接连的10个正整数的7l（l为正整数）次方中，前5个取负，后5个取正，则它们的代数和是5的整数倍。

证明 设n,m为正整数，则由（1）式得

它是5的整数倍。

由（2）得悉，结论对l=1成立，即若a-b是5的整数倍，那么a7-b7也是5的整数倍，现假设l=h（正整数）结论成立，即

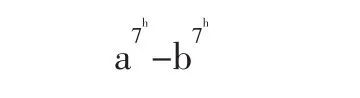
是5的整数倍，那么对于l=h+1时，

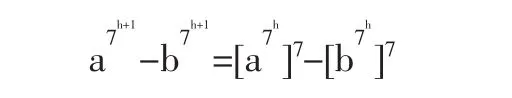
由归纳假设和（2）式得知，它也是5的整数倍，那么总的代数和的自然也是5的整数倍。

证毕。

注意到

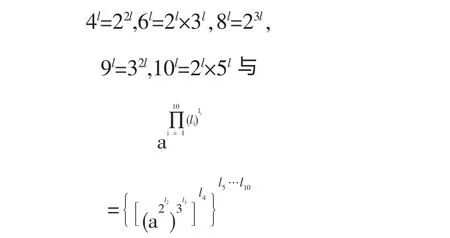
li为正整数，那么有

证明 这是反复应用[定理1-4]和式（2）的直接结果。

证毕。

[定理6] 设h为正整数，则10h个正整数（接连的）的2l,3l,5l,7l次方中（l为正整数）的5h个取负，后5h个取正，则它们的代数和都是5的整数倍（h为正整数）。

证明 设n为正整数，则接连的10h个正整数中，前5h个是

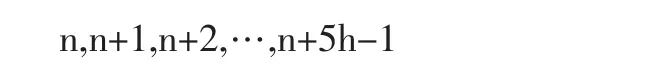
后5h个是

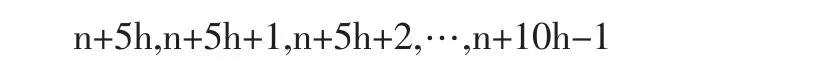
对应项之差都是5h，即是5的整数倍。

由[定理1-4]和式（2），即得结论。

证毕。

[引理2] 接连的10个偶数中，前5个取负，后5个取正，它们的代数和是10的整数倍。

证明 设n为正整数，则接连的10个偶数中，前5个是

后5个是

对应项之差都是10，从而它们的代数和是10的整数倍。

[定理7] 接连的10个偶数的2l,3l,5l,7l,10l(l为正整数）的2l,3l,5l,7l中，前5个取负，后5个取正，则它们的代数和都是10的整数倍。

证明 由式（2），取m=2，类似[定理1-4]的证明，即得结论。

证毕。

证明 由[引理2]和类似[核心定理5]的证明，即得结论。

证毕。

证明 10h个偶数中，前5h个是

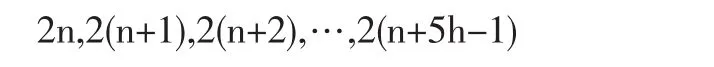
后5个是

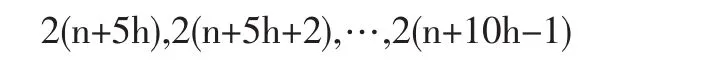
对应项之差都是10h，类似[定理1-4]和式（2）即得结论。

[引理3] 接连的10个奇数中，前5个取负，后5个取正，则它们的代数和是10的整数倍。

证明 接连的10个奇数中，前5个是

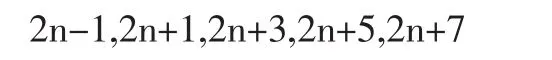
后5个是2n+9,2n+11,2n+13,2n+15,2n+17

对应项之差都是10，那么的代数和是10的整数倍。

证毕。

[定理10] 接连的10个奇数的2l,3l,5l,7l,10l(l为正整数）次方中，前5个取负，后5个取正，则它们的代数和都是10的整数倍。

证明 由[引理3]这个证明完全类似[定理7]的证明。

证毕。

证明 由[引理3]，这个证明完全类似[核心定理8]的证明。

证明 接连的10h个奇数中，前5h个是

对应项之差都是10h，由（2）式和[定理9]的证明，即得结论。

证毕。

［1］王仲才.关于12的神奇特征［J］.江西广播电视大学学报,2012,（2）.

［2］王仲才.关于6的整数倍的第三个神奇特征［J］.江西广播电视大学学报,2012,（4）.