基于光学杠杆原理的炮口扰动角测试方法研究
2013-04-01朱祺,薛挺,郭倩,马娜,兰甸
朱 祺,薛 挺,郭 倩,马 娜,兰 甸
(1.63880部队,河南 洛阳471003;2.63963部队,北京100072;3.北京理工大学光电学院,北京100081)
1 引言
火炮发射过程中的身管振动和弯曲问题,直接影响火炮的射击精度,使火炮性能降低。为了准确评价和考核火炮性能、鉴定火炮质量、提高射击精度,需对火炮发射时的炮口扰动角及其规律进行研究。
由于火炮发射时,膛内火药爆炸形成的高温、高压气体推动弹丸高速运动[1],使身管发生剧烈的高频振动,传统接触式测量方法容易造成传感器脱落损坏,无法达到测量效果。随着光电检测技术的发展,一些非接触式测量方法被用于炮口扰动的测量[2]。然而,火炮身管振动除具有高频的特点外,还具有微小扰动角度和微小横向位移的特点。为了便于测量,需要将微小量进行放大。光学杠杆原理以其放大倍率易于调整、同步性高[3]等优点从常用的非接触式测量方法中脱颖而出。本文提出一种基于光学杠杆原理的炮口扰动角测试方法,并对炮口扰动角数学模型的建立进行详细推导,并对理论模型进行修正讨论,最后通过模拟实验结果,充分验证建模的合理性,为实弹射击实验、测量炮口扰动角及其振动规律提供了重要参考。
2 光学杠杆原理及优势
光学杠杆(Optical lever)是利用光线的镜面反射定律,对微小的角度或位移变化量放大的光学装置。通过对放大位移的测量,间接测量出微小的位移变化以及变化方向[4]。即通过反射的光束在投影屏上的投影点的位移可表示为:

式中,L是被测器件与光电探测器之间的距离。由于角度位移被间距L所放大,所以该原理通常被称为“光学杠杆”原理。
火炮发射时身管振动激烈,无法在身管上安装激光器等不能承受高温高压的光电器件,而只能采用机械方法将金属反射装置固定在身管上,采用光学杠杆原理,即以调制激光光束为信息载体,通过固定在身管上的反射装置使反射激光携带身管振动的信息,一方面由于激光光源和信号接收系统远离火炮,减小了火炮振动对测量结果的影响;另一方面,身管上的反射装置还使出射激光代表的炮口角扩大了一倍,更有利于炮口扰动角的检测。
3 测量系统结构框图及原理
小口径火炮炮口扰动角测试系统主要由脉冲激光光源、平面反射镜、遮光板、PSD[5-6]光电转换与信号处理、数据采集与控制、计算机等部分组成。系统结构原理框图如图1所示。

图1 炮口扰动角测试系统结构
当半导体激光器发出的调制激光由左后侧照射炮口附近的平面反射镜时,携带身管振动信息的反射激光投射到右后侧的漫射屏上;入射光点经光谱滤波和透镜成像后,由PSD转换为位置电流信号;电信号经变换、放大、滤波和数据采集后,由计算机计算出入射光斑的位置,进而获得炮口扰动角测量值。
4 光学杠杆理论模型的建立
由炮口扰动角的测试要求,系统选用二维PSD测量入射到PSD(即漫射屏)上光点的二维平面坐标,但火炮发射时的身管扰动是发生在三维空间范围内的,需将炮口扰动角θ转换为PSD上的二维平面坐标。利用光学杠杆原理测量炮口扰动角,首先需要建立炮口扰动角与漫射屏上激光落点间的数学关系,以便由PSD采集的二维坐标计算出炮口扰动角 θ[7]。
4.1 理论模型
考虑到实际布站及测量的方便,以炮尾为原点,竖直向上为z轴,建立坐标系 O(x,y,z),如图2所示。入射光线l1位于xOy平面内,且与x轴正方向成45°角,炮身长度为R,炮口端点坐标为 M0(x0,y0,z0),通过几何推算,可获得反射光线l2的方向数(l,m,n)。


图2 xOy平面内光线的反射示意图
如图3所示,根据布站要求,接收平面π2应与初始反射光线l20垂直,故π2的方程可表示为:


图3 接收平面π2上的Oνw坐标系
以炮管与x轴的夹角为0°(即炮管无扰动)时,反射光线l20与接收平面π2的交点M20(x20,y20,z20)(即初始位置)为原点建立坐标系Oνw,使ν轴与z轴平行且同向,w轴水平向右,与ν轴组成右手坐标系。
初始反射光线 l20与与平面 π2的交点为M20(x20,y20,z20)。有扰动时,反射光线l2与 π2交点为 M2(x2,y2,z2),经推导可得在 Oνw 坐标系下,炮口端点与接收屏上激光落点M2(w,ν)间的关系:
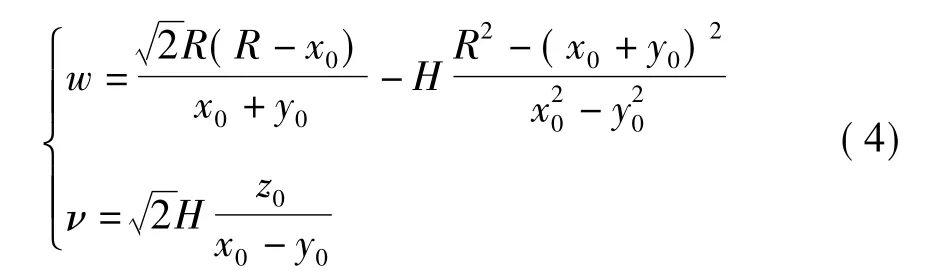
若以炮尾O为原点建立球坐标系(r,θ,φ),即可获得炮口角(θ0,φ0)(即身管指向)与激光落点M2(w,ν)间的关系:

由于火炮发射时,身管振动引起的炮口扰动角θ0较小(振动范围一般小于一倍口径)。例如,对于30 mm火炮,身管长度R=3000 mm,炮口最大扰动角 θ0max=0.57°,可略去 sin2θ0项,有:

式(5)中消去 φ0,有:
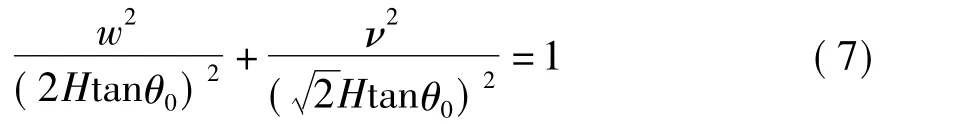
由式(6)看出,若身管扰动角θ0很小且为一常数时,则漫射屏上激光落点的轨迹为长短轴之比a/b槡=2的椭圆,且椭圆的半径随扰动角θ0和观察距离H的增大而增大。
4.2 模型适用范围修正
由火炮发射理论和实验知,火炮发射时振动主要表现为身管振动(炮口绕炮尾转动)和身管弯曲。显然上节的计算是忽略身管弯曲的,因此需对该式是否同样适用于考虑身管弯曲时的情况加以讨论。
如图4所示,P为反射镜初始位置,P″为火炮发射时,身管发生振动和弯曲后反射镜的位置,且P″不与身管垂直。M为接收屏位置,H则为经P″发射后的激光投影至接收屏M上的点位。
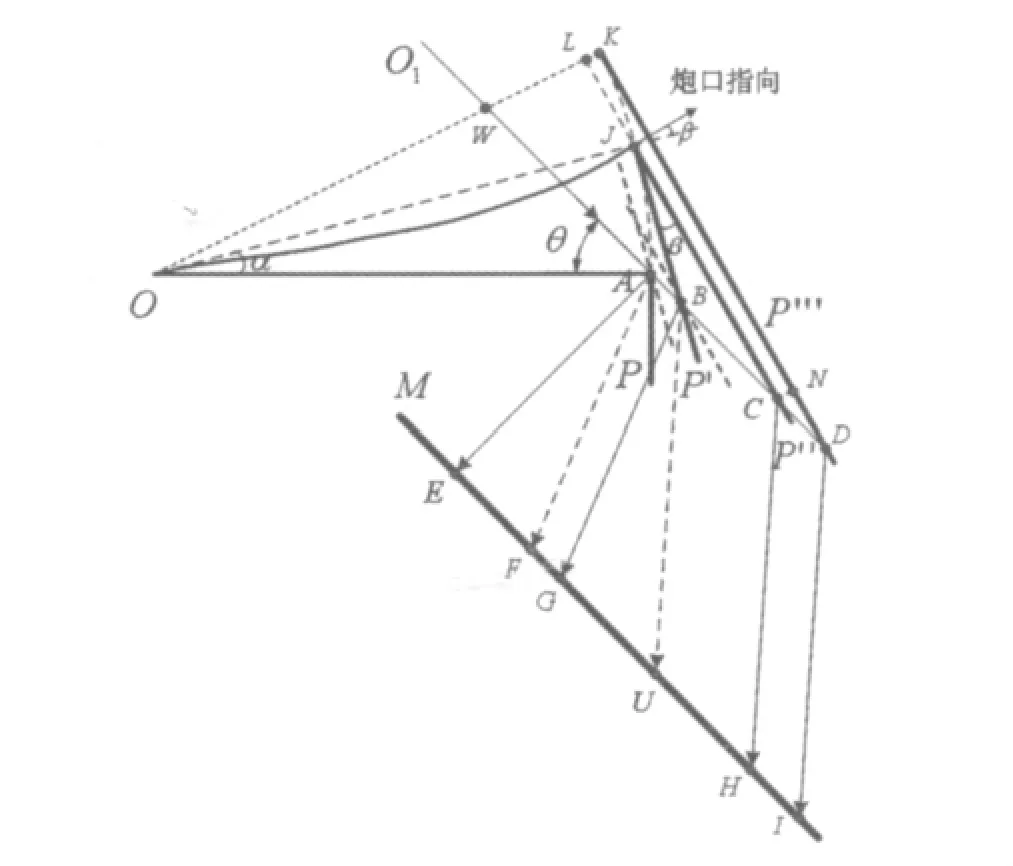
图4 考虑身管弯曲时的炮口角计算
考虑到身管弯曲引起身管长度的变化很小,由此产生的P″的平移可以忽略,则身管振动与身管弯曲所产生的炮口扰动角的改变就可认为由两次转动组成(即图4中的转动角度α和β)。为了简化计算,我们将第二次转动近似为身管绕炮尾由位置J再旋转角度β,到达位置K,此时,反射镜 P与不作近似时的反射镜P″平行。
通过计算可得出用反射镜P代替反射镜P″时,反射光线在接收屏M上的投射点H与I间的偏差HI=1.5 mm。事实上,当身管振动+身管弯曲使反射镜移至位置P″时,接收屏M上激光点的位移为EH,其中FG,UH为反射镜平移产生的位移(与接收屏M到反射镜的距离无关);而EF,GU为反射镜转动角度α,β产生的位移(随接收屏M到反射镜的距离增大)。且经计算,EF=99.5 mm,GU=400 mm。
显然,HI与EH相比可以忽略,由此得到重要推论:由于身管弯曲产生的身管长度变化可忽略不计,而将火炮身管的振动过程等效为炮口在以身管尾部O点为原点、身管长度R为半径的球面上运动。
5 模拟原理实验验证
为了验证上一节推导的炮口扰动角与漫射屏上落点间关系,设计了“跑口扰动角-漫射屏落点”原理实验。
5.1 实验过程及原理
该实验的器材主要有激光脉冲调制驱动电路、650 nm半导体激光器、平面反射镜(模拟身管振动)、漫射接收屏、步进电机控制与驱动电路、Mgea16单片机控制电路等。
半导体激光器在脉冲激光电源和单片机的控制下产生脉冲激光,激光束经透镜会聚后照射到由步进电机带动的、有一定固定倾角的平面反射镜上,经反射后照射到漫射接收屏上形成明亮的激光光斑。当平面反射镜在步进电机带动下以一定的角速度旋转(即模拟火炮振动时,炮口绕水平轴线作圆周运动)时,在漫射屏上形成炮口角运动轨迹,利用相机长曝光拍摄下轨迹照片。同时通过VB软件绘制出炮口扰动角与漫射屏上落点坐标间关系(即式(4))的理论曲线,两者对比。
5.2 实验结果与分析
如图5所示,根据式(5),通过计算机绘制出理论曲线。其中身管长度为3 m,平面反射镜到漫射屏的距离为5 m,入射角为45°,每条曲线间的炮口扰动角增量为2.5°,最大炮口扰动角为25°。

图5 炮口扰动角与漫射屏落点坐标理论曲线
图6 为通过相机长曝光后拍摄下的漫射目标板上形成的炮口扰动角运动轨迹。

图6 模拟炮口扰动角与漫射屏落点实验轨迹
由于实验条件的局限和激光落点轨迹的动态性,没有对实验条件和实验结果进行定量测量,但对比图5和图6不难看出,图6的激光落点(动态)的轨迹与图5中的曲线非常相似,说明上一节中推导的火炮炮口扰动角与接收屏上落点的关系是正确的,印证了光学杠杆理论模型的合理性、准确性。
另外,考虑到火炮实际发射时身管振动的角度较小(约0.53°,与1倍口径对应),即使加上身管弯曲的角度(约1.5°),也小于 3°~5°的实际情况,图7示出了炮口扰动角增量为0.5°,最大角度为5°的10条曲线。显然,当炮口扰动角较小时,激光落点轨迹非常近似于椭圆曲线,这为进行实弹射击,测量火炮炮口扰动角及其振动规律提供了重要参考。

图7 火炮小扰动角(<5°)与漫射屏落点坐标理论曲线
6 结论
根据当前火炮发射实验、鉴定要求和非接触测量发展及现状,结合光学杠杆基本原理,应用现代光电检测技术,设计了一种非接触式小口径火炮炮口扰动角测试系统。针对小口径火炮发射过程中的振动规律,建立了炮口扰动角与PSD二维坐标间的数学模型,并对理论模型的适用范围进行了修正,使之更符合身管振动的实际情况,并在实验室条件下搭建模拟实验验证系统。实验结果表明实际拍摄到的炮口扰动角与漫射屏落点轨迹和计算机绘制出的理论曲线非常相似,印证了光学杠杆理论模型的合理性、准确性。这一结论,为系统测试功能的最终实现奠定了坚实的数学基础,为测量火炮炮口扰动角及其振动规律提供了重要参考。
[1] O uyang Guangyao,Wang Shuzong,Wang Deshi.Investigation of barrel vibration and reducing vibration[J].Journal of Naval Academy of Engineering,1999,(2):79 -86.(in Chinese)欧阳光耀,王树宗,王德石.火炮身管振动特性及减振研究[J].海军工程学院学报,1999,(2):79-86.
[2] C hen Yanhui,Guo Min,He Zongying,et al.Muzzle vibration testmethod and practice[J].Journal of Gun Lanch &Control,2010,3:80 -83.(in Chinese)陈彦辉,郭旻,何宗颖,等.炮口振动测试方法及实践[J].火炮发射与控制学报,2010,3:80 -83.
[3] L u Guangwen,RuiXiaoting,Gu Jinliang,etal.Testand analysis of attitude and movement of projectile in bore[J].Acta Armamentarii,2006,27(1):149 -153.(in Chinese)陆文广,芮筱亭,顾金良,等.弹丸膛内姿态与纵向运动测试与分析[J].兵工学报,2006,27(1):149 -153.
[4] E iji Higura Shi,Renshi Sawada,Takahiro Ito.Monolithiangulation and optical beam deflection[J].Applied Optics,1999,38(9):1746 -1751.
[5] Tao Zhongxiang,Song Jianzhong.Experimental research of influence of load resistance on tetra-lateral position sensitive detectors[J].Laser & Infrared,2005,35(2):115 -117.(in Chinese)陶忠祥,宋建中.负载电阻对四边形PSD的影响实验研究[J].激光与红外,2005,35(2):115 -117.
[6] Zhao Ailing,Zhang Haifeng.Design of new tupe of touchpad based on the optical sensor[J].Laser & Infrared,2011,41(10):1159 -1162.(in Chinese)赵爱玲,张海峰.一种基于光学传感器的新型触摸板的设计[J].激光与红外,2011,41(10):1159 -1162.
[7] Zhang Zhiquan,Zhu Qi,Ding Sheng,etal.Ameasurement method ofmuzzle disturbance based on PSD[J].Journal of Academy Force Engineering,2012,26(2):49 -53.(in Chinese)张智诠,朱祺,丁晟,等.基于PSD的炮口扰动测试方法[J].装甲兵工程学院学报,2012,26(2):49 -53.
