经验公式在家电仿真设计与研究中的应用

蒋皓静 冯静 吴晓丽

（中国家用电器研究院 北京 100176）

在进行家用电器的仿真设计与研究时，经常需要根据相关变量的实测数据和历史资料建立变量间关系的数学表达式，进行预测与分析。例如在研究冰箱蒸发器温度分布规律的模拟，温度场和流场的仿真，电机绕组的温升测定等。从一组实验数据出发，寻求函数的近似表达式，这个近似表达式就称为经验公式。

1 最小二乘法基本原理

为得到经验公式需要进行数据拟合。数据拟合的具体作法是：对给定数据(x，y ) (i=0,1,…,m)，在取定的函数类Φ中，求p(x)∈Φ，使误差：r=p(x)-y (i=0,1,…,,m)的平方和最小，即：

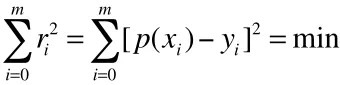
从几何意义上讲，就是寻求与给定点(x，y)(i=0,1,…,,m)的距离平方和为最小的曲线y=p(x)（图1）。函数p(x)称为拟合函数或最小二乘解，求拟合函数p(x)的方法称为曲线拟合的最小二乘法。

2 多项式拟合原理

假设给定数据点(x，y) (i=0,1,…,,m)，Φ为所有次数不超过n(n≤m)的多项式构成的函数类，现求,使得：

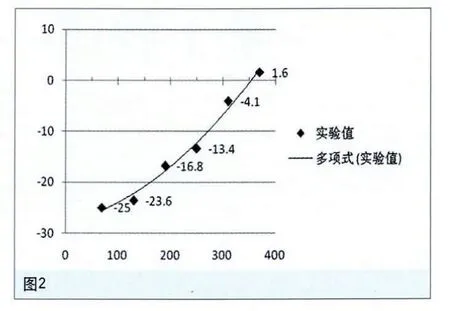
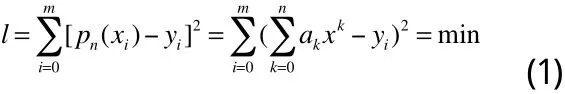
当拟合函数为多项式时，称为多项式拟合，满足式（1）的p (x)称为最小二乘拟合多项式。特别地，当n=1时，称为线性拟合或直线拟合。

式（3）或式（4）称为正规方程组或法方程组。

可以证明，方程组（4）的系数矩阵是一个对称正定矩阵，故存在唯一解。从式（4）中解出a(k=0,1,…,n )，从而可得多项式：

可以证明，式（5）中的p (x)满足式（1），即p (x)为所求的拟合多项式。把称为最小二乘拟合多项式p(x)的平方误差，记作：

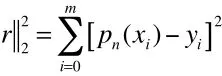
由式(2)可得

在实际应用中，n＜m或n≤m；当n=m时所得的拟合多项式就是拉格朗日或牛顿插值多项式。

3 具体应用举例

3.1 应用一

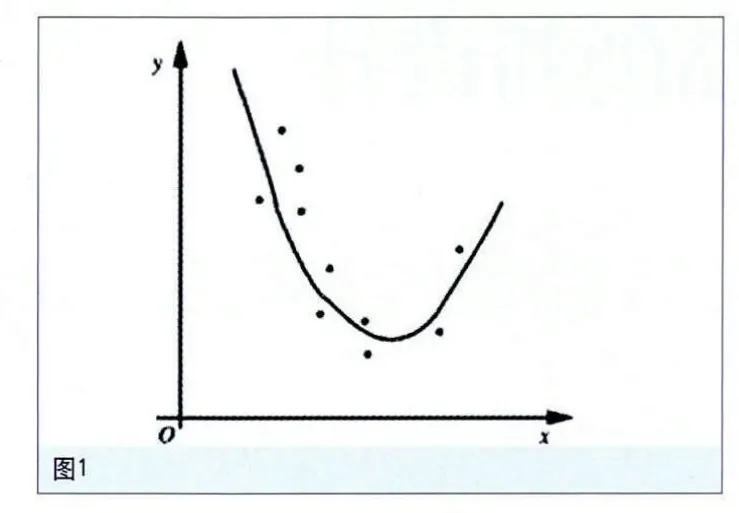
某导线在温度T (℃)时的电阻R(Ω)如表1，电阻R与温度T有近似函数关系。

由图2可见，测得的数据接近一条直线，故取n=1，拟合函数为。列表如表2。矩阵方程组为：

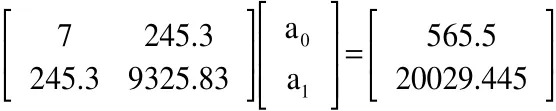
解矩阵方程组得：

故得R与T的拟合直线为:

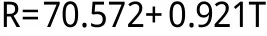
利用上述关系式，可以预测不同温度时的电阻值。如，由R=0得T=-242.5，即预测温度T=-242.5℃时，此导线无电阻。

3.2 应用二

冰箱中蒸发器的形式、位置和温度对冰箱的性能和食品的保藏有着重要的影响。蒸发器温度边界条件的指定也有重要意义。在默认情况下通常指定壁面温度为常数，而实际上蒸发器表面的温度往往沿着高度方向有比较大的变化。其中一组数据如表3所示。

由图3取n=2，设拟合曲线方程为：

得正规方程组：

解得：

故拟合多项式为：

由此可知在冰箱间室内上下温度差较大,存在着不利于储存食物的问题（见图3）。

4 结语

本文对研究中的实际问题建立数学模型，所用原始数据容易获得，采用数值分析方法简便可靠，运用所得到的经验公式进行预测分析对于设计与研发有指导作用。

表1 导线在温度T(℃)时的电阻R(Ω)

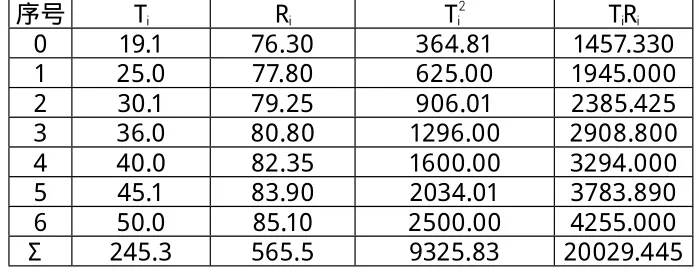
表2 应用一测试数据

表3 蒸发器表面温度

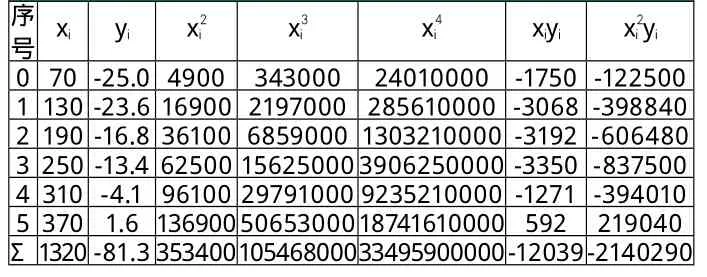
表4 应用二测试数据

[1] 于楠.用于直冷式和间冷式家用冰箱性能预测的数学模型[J].制冷技术,2011，04

[2] 吴小华. 冰箱冷藏室温度场和流场的仿真与优化[J].北京石油化工学院学报, 2006，03

[3] 杨沫.家用冰箱冷冻、冷藏室温度场的数值计算[J].制冷学报, 1991,04