四元数法改善复杂曲面5轴加工精度研究
2013-03-31于洋邓勇生潘琳
于洋,邓勇生,潘琳
(1.西安石油大学机械工程学院,陕西西安710065; 2.中国航天科技集团公司第四研究院第四十四研究所,陕西西安710025)
自由曲面广泛地应用于现代工业设计中,例如航空、航天、汽车、模具等。5轴数控加工给复杂自由曲面的加工带来了更多的灵活性、高效率以及良好的精度表现,可以处理三轴机床无法加工的曲面[1-2]。然而,5轴数控加工仍有许多问题有待解决和改进,比如刀轴控制就被认为是数控编程中最困难的问题之一,主要是由于5轴加工中刀具运动的复杂性和复杂自由曲面曲率分布的不规则所致。在5轴加工中,由于刀具方向的不断变化,当刀具轴向过度依赖被加工曲面几何时,容易产生刀具轴向变化剧烈,从而导致过切、碰撞以及切削误差过大的情况。因此,要充分发挥5轴数控加工的优势,必须解决刀轴过度依赖曲面几何导致变化剧烈这一瓶颈问题。
近年来,国内外学者对此做了许多工作,然而大多数都集中在处理避免过切干涉的发生及其修正上[3-6]。对于加工精度的要求,通常都是通过增加刀具接触点的方式达成,虽然的确能够提高加工精度,但是会造成NC数据过于庞大的问题,很少有通过调整刀具轴向来达到避免过切、提高精度的文献。MORISHIGE等[7]应用2-Dimensional C-Space的方法,将傾斜角 (Lead Angle)及偏摆角 (Tilt Angle)映射至C-Space上,求取合理刀具轴向,但对于自由曲面,须将曲面离散成细小平面再做计算,效率很低。文献[8-9]通过寻找可行性的刀具方向来控制曲面加工误差,效率较低。文献 [10]提出了通过设置权重的方式来进行刀具轴向的均匀化分配,但对其中的干涉检查和处理分析不透,并没有从理论和方法上进行创新和突破。基于此,作者提出了一种新的刀具轴向设计算法,该方法根据曲面的微分几何特性,通过制定可能发生过切处的刀具轴向,藉以计算其他位置的轴向,同时进行过切、干涉检查及处理,提高切削效率,保证曲面的加工精度和加工质量。
1 刀具轴向设计考量及初始位置
1.1 刀具轴向设计考量
考虑到5轴加工中,设计不合理的刀轴方向会导致机床震动、切削误差过大、过切、碰撞以及加工不完整的情况发生,因此,设计刀具轴向时必须要满足以下条件:(1)刀具轴向的设计必须考虑过切、碰撞的情况;(2)同一条刀具路径上,两个刀具接触点之间的刀具轴向变化量应该尽可能小。因此,作者提出了通过指定可能发生过切、干涉区域的刀具轴向,再依据四元数插补方法,计算出其余位置刀具轴向的方法。
1.2 刀具初始位置
设定当前刀具接触点 (CC点)坐标为C(xC,yC,zC),过点C的曲面切平面可表示如下:

其中[A,B,C]为切平面的单位法矢,也是刀具轴向的单位方向矢量,可表示如下:

其中:P(u,v)为曲面上任一点的矢量,u、v为变量,则曲面上任意一点可由直角坐标系的分量x(u,v)、y(u,v)、z(u,v)来表示。
在重要区域的刀具轴向的指定方法上,为了几何上计算简便,并且可以进行严谨的刀具碰撞的检测,作者提出以曲面上CC点处的法线方向作为基准,在刀具前进方向,倾斜某一角度θ来得到刀具初始位置,如图1所示。

图1 初始刀具轴向
2 四元数内插法
四元数 (Quaternion)最初的理论是以一对三维空间向量之间的角度关系定义,近年来则常被应用在电脑图形学及机器人学上,用来描述运动方式。
一个四元数q中包含4个元素,定义如下:

其中:qx,qy,qz,qw为实数,i,j,k则是符合以下规则的坐标轴:

qw称为纯量部分,而(qx,qy,qz)称为向量部分。

图2 四元数插补法
四元数算法不仅支持相同的旋转速度,而且在大圆弧上的插补向量连接两个边界向量,如图2所示。给定两个指定的刀轴方向V1(V1x,V1y,V1z)、V2(V2x,V2y,V2z),对于从V1(V1x,V1y,V1z)、V2(V2x,V2y,V2z)的四元插补方程V(n)可以表示如下:

其中:参数n为插V1与V2之间的向量,θ= cos-1(V1·V2)
使用四元数插补法对图3中所指定的刀具轴向进行其余刀具轴向插补,插补后的刀具轴向分布如图4所示,图5显示了刀具轴向变化角度的比较图,可以看出:四元数插补法可以提供光顺的刀轴变化,并且不会产生不需要的刀轴扭曲和跳动。

图3 指定特定位置刀具轴向
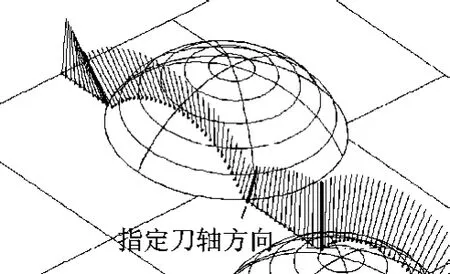
图4 四元插补法所生成的刀具轴向
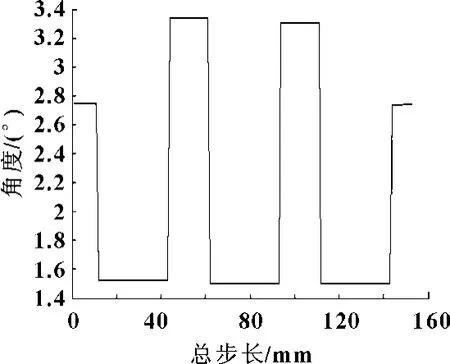
图5 四元数插补法刀具轴向变化
3 干涉刀位的修正
在完成刀具轴向设计之后,则需要对每一个刀具轴向来进行刀具干涉侦测。就空间几何来看,直接计算检查点到刀具的垂足距离d并判断,若其垂足距离d小于刀具半径D/2,则表示发生刀具碰撞;反之,若其垂足距离d大于刀具半径D/2,则无碰撞。

图6 碰撞示意及参数定义
假设刀具轴向的旋转中心为P1(x1,y1,z1),端点为P2(x2,y2,z2),而检查点为PZ(x3,y3,z3),如图6所示,可以用参数a表示成参数式:

令Δx1=x2-x1、Δy1=y2-y1、Δz1=z2-z1得:

接下来计算检查点到刀具中心的垂足点P(x(a),y(a),z(a))的距离d:

将式(8)代入式(7)得:

令Δx2=x3-x1、Δy2=y3-y1、Δz2=z3-z1,式(9)可如下表达:

又点PZ到刀具中心轴的垂足距离为最短距离,所以:

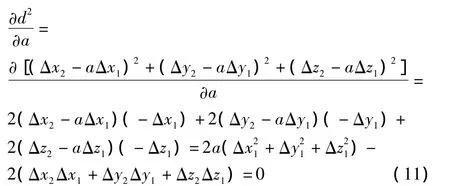
最后求得的a为:

将所得的a代入式 (7)求检查点PZ到刀具中心轴的垂足点P,而PZ到刀具中心轴的垂足距离d亦可求得。最后判断若垂足距离d小于刀具半径D/2,则发生刀具碰撞亦检查点PZ为碰撞点;若垂足距离d大于刀具半径D/2,则检查点PZ不是碰撞点。
4 算例分析
为了更好地验证文中所提出的刀轴设计算法,作者使用主轴旋转式5轴机床进行切削实验。实验将针对两种不同的刀具轴向设计方式:传统法向法与四元数插补法,对比两种加工方法的切削误差,并进行探讨。加工条件如表1所示,曲面模型如图7所示,采用等参数加工法,机床型号为Mazak5轴立式加工中心500-5X。

表1 加工条件
图8为使用四元数插补法所设计的刀具轴向分布图,图9为使用传统的法向刀具轴向设计方法所生成的刀具轴向。可以明显看出:使用传统方法所设计的刀轴变化较为剧烈,刀轴角度平均变化量大概在25°左右,最大的变化量达到了58°;使用四元数插补法设计的刀轴角度变化不超过4°,很适合用来进行刀具轴向规划。

图7 实验所使用模型

图8 四元数法设计刀具轴向

图9 法向法所生成刀具轴向
图10显示了采用法向刀轴方法加工轮廓时切削误差变化图;图11显示了采用四元数刀轴方法加工轮廓时切削误差变化图。可以看出:法线加工方法误差较大,已经超过设定误差0.02 mm,加工效果不理想,这是由于刀具轴向变化较为剧烈所引起;而四元数法对误差控制较好,均小于设定误差emax=0.02 mm,较传统方法有大幅度的改进。

图10 法向刀轴切削误差

图11 四元数插补刀轴切削误差
5 结论
通过使用四元数插补算法,解决了5轴自由曲面加工中刀轴变化剧烈的问题,并且根据刀具半径与检查点到刀具的垂足距离判断刀具是否与曲面发生干涉,成功地解决了刀轴光顺与曲面干涉的检测与修正这一5轴数控加工中的瓶颈问题。算法的运用结果表明:该算法效率高,精度易于控制,可用于叶轮类对刀轴变化敏感且干涉较为严重的5轴加工中。
【1】LEE Y S,CHANG T C.2-Phase Approach to Global Tool Interference Avoidance in 5-axis Machining[J].Computer-Aided Design,1995,27(10):715-729.
【2】YOU C F,CHU C H.Tool-path Veri Cation in Ve-axis Machining of Sculptured Surfaces[J].The International Journal of Advanced Manufacturing Technology,1997,13(4): 248-255.
【3】HWANG Y R,HO M C,HU C H.Five-axis Tool Path Generation Based on Discrete Point Data[C]//Proc Precision Machinery Manufacturing Conference,Taipei,2001:149-153.
【4】HO M C,HWANG Y R.A New Decision Algorithm of Maximum Allowable Step Length for 5-axis Table-tilting Type Machining[J].Journal of the Chinese Institute of Engineers,2002,25(2):233-242.
【5】BALASUBRAMANIAM M,HO S,SARMA S,et al.Generation of Collision-free 5-axis Tool Paths Using a Haptic Surface[J].Computer-Aided Design,2002,34:267-279.
【6】张和明,张玉云,熊光楞.复杂曲面5坐标数控加工干涉检查及刀位修正[J].清华大学学报:自然科学版,1998 (2):65-68.
【7】MORISHIGE K,KASE K,TAKEUCHI Y.Tool Path Generation Using C-Space for 5-Axis Control Machining[J].Trans of the ASME,J of Manufacturing Science and Engineering,1999,121(1):144-149.
【8】LEE Y S.Mathematical Modeling Using Different End Mills and Tool Placement Problems for 4-and 5-axis NC Complex Surface Machining[J].International Journal of Production Research,1998,36(3):785-814.
【9】LEE Y S.Non-isoparametric Tool Path Planning by Machining Strip Evaluation for 5-axis Sculptured Surface Machining[J].Computer-Aided Design,1998,30(7):559-570.
